ここではマクスウェル – ファラデーの式について説明します。
一般的にはファラデーの電磁誘導の法則という呼称がよく知られていると思いますが、本ページではマクスウェル – ファラデーの式とは完全に同一ではなく、ここでは区別します（0章参照）。
マクスウェル – ファラデーの式は以下です。
微分形
$$ \nabla \times \boldsymbol{E} = – \frac {\partial \boldsymbol {B}} {\partial t} $$
積分形
$$ \oint_l \boldsymbol{E} \cdot d\boldsymbol {l} = -\frac {d}{dt} \int_S \boldsymbol{B}\cdot d\boldsymbol{S}$$
0 名称と構成
本ページでは以下のように名称と適用範囲を決めます。
ファラデーが発見した電磁誘導に関する法則は一般的に「ファラデーの電磁誘導の法則」とよばれます。本ページもこの名称を使います。ファラデーは定量的にこれを表しませんでしたが、後年、マクスウェルが定式化しました。この式を本ページでは「マクスウェル – ファラデーの式」とよぶことにします。
マクスウェルの方程式の一つであるのはマクスウェル – ファラデーの式です。本ページの目的もこの式の説明です。
本ページではファラデーの電磁誘導の法則とマクスウェル – ファラデーの式は意味が異なるものとします。前者が後者を包含します。しかし、より知られているのは前者であるので、これについても説明します。
本ページは以下の構成とします。
1 マクスウェル – ファラデーの式
2 ファラデーの電磁誘導の法則
3 前章の補足
4 まとめ
前述の通り両者が明確に分かれるわけではありませんが、2章は1章の範囲外のところを中心に説明します。
1 マクスウェル – ファラデーの式
1.1 微分形
微分形の左辺ではベクトル場における「回転」が使われています。まずこの意味を理解し、その後で右辺との関係を考えてみましょう。
1.1.1 回転の意味
微分形の左辺の\(\nabla \times\)はベクトル場における回転を示しています。
回転とは 対象とする点の周辺の非線対称成分を単位面積当たりに換算（正規化）したベクトルです。
詳細は下の「＋」（アイコンが化けているかもしれません）を押して表示させてください。
また、「ベクトル場の回転」にもう少しくわしく書いていますのでよければこちらもご覧ください。
(1)回転の定義
以下が回転の定義です。
$$\nabla \times \boldsymbol {E} = ( \frac {\partial {E_y}} {\partial {x}} – \frac {\partial {E_x}} {\partial {y}} ) \boldsymbol {k} $$
\(\boldsymbol {E}\)は電場、\(E_x\)、 \(E_y\)はそれぞれ\(\boldsymbol {E}\) の \(x\)、\(y\)成分（スカラー）です。 \(\nabla \times \boldsymbol {E}\)は\(x\)、\(y\)とは垂直です。
\(\boldsymbol {k}\)は\(x\)、\(y\)と垂直な単位ベクトルです。\( \nabla \times \)はこの後に続くベクトル場の回転を意味します。
\( \nabla \times \)ではなく\(\boldsymbol{rot}\)や \(\boldsymbol{curl}\) を使う場合もあります。
(2)方針
回転とは図のような、点の周辺の非線対称な成分をベクトルで示したものです。
図のように微小な正方形があるとします。図には描いていませんが、この正方形の内外に電場が存在します。\(\boldsymbol {k}\)は\(\nabla \times \boldsymbol {E}\)と同じ方向の単位ベクトルです。
真上から見ると図のようになります。\( \nabla \times \boldsymbol {E} \)は画面奥から手前の方向です。
正方形の境界に沿って\(\boldsymbol{E}\)の成分を求めます。ただし絶対的な値ではなく、向かい合う辺の成分との相対値（以降、「非線対称成分」とよぶことにします）として求めます。 そしてこの結果を回転の定義と照らし合わせ関係を求めます。
(3)2点の非線対称成分
2辺の各1点に存在する電場の非線対称成分を求めます。
両者の電場の差はどうすれば求まるでしょう。
下の図の正方形の上に描かれた部分に注目してください。これは横軸が\(x\)、縦軸が\(\boldsymbol{E}\)の差分のグラフを表しています。 傾きは\(\displaystyle \frac {\partial {E_y}} {\partial {x}}\)、横幅は\(\Delta{x}\)です。
つまり、両者の差は
$$\frac {\partial {E_y}} {\partial {x}} \Delta{x} $$
です。
(4)縦方向の2辺の非線対称成分
前節では「2点」の非線対称成分を求めました。次に「2辺」について非線対称成分を求めます。
正方形内外の電場は一様とは限りません。本来は\(\displaystyle \frac{\partial E_y}{\partial x} \Delta x\)を線積分すべきところですが、微小な領域であるため一様であるとして近似で表します。
一様であれば、前節で求めた式に\(\Delta y\)を掛けるだけです。つまり、
$$\frac {\partial {E_y}} {\partial x} \Delta x \Delta y$$
です。
(5)横方向の2辺の非線対称成分
横方向についても同じように求めることができます。 まず「2点」間の非線対称成分は、以下です。$$- \frac {\partial {E_x}} {\partial {y}} \Delta{y} $$
\(\displaystyle \frac {\partial {E_x}} {\partial {y}}\)は上方向にいくほど右に増加する場合を正としています。 しかし今求めたいのは反時計回りなので上の辺は下の辺に比べてより左を向いていなければなりません。 したがってマイナスの符号がつきます。
これに\(\Delta{x}\)を掛ければ「2辺」の非線対称成分を求めることができます。$$- \frac {\partial {E_x}} {\partial {y}} \Delta{y}\Delta{x} $$
$$\left(\frac {\partial {E_y}} {\partial {x}}- \frac {\partial {E_x}} {\partial {y}} \right) \Delta{x}\Delta{y} $$
となります。回転の定義式と比較してください。上記式より\(\Delta x \Delta y \)を除けば等しくなります。 \(\Delta x \Delta y \)は正方形の面積なので、これで割るということは単位面積当たりであるということを示しています。
以上より、冒頭の結論が導かれます。
単位面積当たりというところが直観的ではないと思いますが、積分形との関係のところで述べます。
1.1.2 右辺の物理的意味
微分形の右辺にどのような意味があるか考えてみましょう。
\(\displaystyle \frac {\partial \boldsymbol {B}} {\partial t} \)は磁場\(\boldsymbol{B}\)を時間で偏微分したベクトルです。
例えば、以下のように対応します。
\(\boldsymbol{B}\) が上を向いていて、その大きさが増加しているとき、\( \displaystyle \frac {\partial \boldsymbol {B}} {\partial t} \)は 上を向く
\(\boldsymbol{B}\) が上を向いていて、その大きさが減少しているとき、\( \displaystyle \frac {\partial \boldsymbol {B}} {\partial t} \)は 下を向く
\(\boldsymbol {B}\)が止まっているとき \( \displaystyle \frac {\partial \boldsymbol {B}} {\partial t} \) の大きさは0です。
ベクトル場の回転は、ベクトルが時計回りになるように見たとき、手前から奥へ向きます。つまりネジを閉めるときに回す方向とネジが進む方向の対応です。
これに負号がつくので、
\(\boldsymbol{B}\) が上を向いていて、その大きさが増加しているとき、電場は上から見て時計回り
\(\boldsymbol{B}\) が上を向いていて、その大きさが減少しているとき、電場は上から見て反時計回り
です。下向きも同様です。
図の緑色は\(\boldsymbol{B}\)、赤または青の円は\(\boldsymbol{E}\)です。円は向きによって色を変えています。
1.1.3 \(\boldsymbol{B}\)の時間変化がある点のみに\(\boldsymbol{E}\)が発生する？
定義（下記）の通り、非対称な成分があった点でのみ回転は発生します。
$$\nabla \times \boldsymbol {B} = ( \frac {\partial {B_z}} {\partial {y}} – \frac {\partial {B_y}} {\partial {z}} ) \boldsymbol {i} + ( \frac {\partial {B_x}} {\partial {z}} – \frac {\partial {B_z}} {\partial {x}} ) \boldsymbol {j} + ( \frac {\partial {B_y}} {\partial {x}} – \frac {\partial {B_x}} {\partial {y}} ) \boldsymbol {k}
$$
上記1.1.2の図は\(\boldsymbol{B}\)と\(\boldsymbol{E}\)の間隔があるように描いていますが、実際には変化のあった\(\boldsymbol{B}\)と回転を示す\(\boldsymbol{E}\)の距離は無限小です。それ以外の場所では\(\boldsymbol{B}\)の時間変化によって\(\boldsymbol{E}\)の回転は生じません。
\(\boldsymbol{B}\) の変化によって同心円状に \(\boldsymbol{E}\)が生じるようなイメージをもちませんか。これについては1.4節で述べます。
1.2 積分形
改めて積分形です。
$$ \oint_l \boldsymbol{E} \cdot d\boldsymbol {l} = -\frac {d}{dt} \int_S \boldsymbol{B}\cdot d\boldsymbol{S}$$
閉曲面を\(S\)、境界を\(l\)とします。これは何らかの実体がなければならないというものではなく、空間上で定義した仮想の領域です。
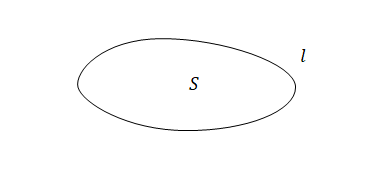
曲面\(S\)に磁場\(\boldsymbol{B}\)があるとします。図では一様であるように描いていますが、一様である必要はありません。
時間微分を領域\(S\)内で面積分します。式では面素（\(S\)の微小領域を示すベクトル）を\(d\boldsymbol{S}\)とします。これが左辺です。\(\boldsymbol{B}\)の大きさそのものではなく、\(S\)の垂直成分が積分の対象になる点に注意ください。
\(\boldsymbol{B}\)の大きさ・向きが変化したとします。
\(\boldsymbol{B}\)が時間経過とともに変化することにより\(\boldsymbol{E}\)が生じます。\(\boldsymbol{E}\)を\(l\)に沿って線積分します。式では線素（\(l\)の微小区間を示すベクトル）を\(d\boldsymbol{l}\)としています。これが右辺です。
向きと符号について確認しましょう。
図において上向きを正と定めたとします。その場合、線積分の方向は下から見て時計回り、つまり右ねじを締める方向です。ただしファラデーの法則の場合は右辺に負号がつきます。
まず右辺についてです。\(\boldsymbol{B}\)は時間経過とともに上向きの成分が減少しています。つまり時間について偏微分をするとそのベクトルは下を向きます。単位法線ベクトルは上を向くので面積分すると、負になります。これに負号がつくので右辺は正です。
次に左辺です。右辺が正であったので、左辺も正でなければなりません。線積分の方向は下から見て時計回りであったので、（平均すると）\(\boldsymbol{E}\)は下から見て時計回りになります。
1.3 微分形と積分形が等しいことの直観的な確認
ガウスの法則のページでは発散定理を使って微分形と積分形が同じ意味であることを確認しました。
似た方法で、ファラデーの法則の微分形と積分形はストークスの定理を使って確認することができます。
1.3.1 ストークスの定理
ストークスの定理は以下です。
$$ \int_S \nabla \times \boldsymbol {F} \cdot d\boldsymbol{S} = \oint_l \boldsymbol{F} \cdot d\boldsymbol {l} $$
\(\boldsymbol{F}\)はベクトル場、\(S\)は平面、\(l\)は平面の境界です。
下のように微小領域の境界で線積分をすることを考えます。矢印は線積分の向きです。
微小領域が2個並んでいる場合、その線積分の和はどれだけになるでしょう。
両者が接しているところだけに注目してみましょう。下の図の黒い線です。線積分の向きが反対なので、和を求めると、この部分は相殺されます。したがって両者の線積分の和は赤い部分のみの経路の結果です。つまり並んだ図形の外形です。
縮小して改めて並べてみましょう。
下の図の赤い線が線積分の経路です。
2個並べました。両者が接する線は流出が相殺されます。黒い線が相殺される線です。
数を増やしました。線積分をするのは周辺の赤い線のみです。
下の図は四角を無限に小さくし無数に並んだ状態です。
微小領域の回転の総和とは面積分のことです。つまり、領域内の回転の面積分が境界の線積分と等しいことが確認できました。
1.3.2 ストークスの定理の、ファラデーの法則への適用
改めて、微分形、ストークスの定理、積分形です。
微分形
$$ \nabla \times \boldsymbol{E} = – \frac {\partial \boldsymbol {B}} {\partial t} $$
ストークスの定理
$$ \int_S \nabla \times \boldsymbol {F} \cdot d\boldsymbol{S} = \oint_l \boldsymbol{F} \cdot d\boldsymbol {l} $$
積分形
$$ \oint_l \boldsymbol{E} \cdot d\boldsymbol {l} = -\frac {d}{dt} \int_S \boldsymbol{B}\cdot d\boldsymbol{S}$$
微分形の両辺を\(S\)で面積分すると、左辺は以下です。
$$ \int_S \nabla \times \boldsymbol {E} \cdot d\boldsymbol{S}$$
ストークスの定理を適用すると、以下と等しくなります。
$$ \oint_l \boldsymbol{E} \cdot d\boldsymbol {l} \quad \quad (1)$$
微分形の右辺の面積分は
$$- \int_S \frac {\partial \boldsymbol {B}} {\partial t} \cdot d\boldsymbol{S} $$
となります。
この被積分関数に時間微分があります。時間微分を外へ移動します。
$$ -\frac {d}{dt} \int_S \boldsymbol{B}\cdot d\boldsymbol{S} \quad \quad (2)$$
ただし、\(S\)が時間によって変わらないことが条件です。\(S\)が固定であれば上の式に変換できます。
\(S\)が変動する場合はこの限りではありません。\(\boldsymbol{B}\)の大きさが0ではなく、かつ時間により変化しない場合を考えてみてください。時間経過とともに\(S\)が変わることによって面積分も変わるはずです。2.4節にてこのことに関連し述べます。
偏微分が微分に変わるのは、位置が変数でなくなるからです。磁場は\(\boldsymbol{B}(\boldsymbol{r},t)\)と表せますが、面積分した後の磁場は\(\Phi (t)\)と、位置に依存しない関数になります。
さて、\(S\)が固定であったとします。\((1)=(2)\)より
$$ \oint_l \boldsymbol{E} \cdot d\boldsymbol {l} = -\frac {d}{dt} \int_S \boldsymbol{B}\cdot d\boldsymbol{S}$$
これは積分形と同一です。以上より微分形と積分形が同じ意味であることが確認できました。
1.3.3 微分形の「単位面積当たり」の意味
1.1節で回転は「単位面積当たりの非線対称成分」であると述べましたが、これはどのような意味があるのでしょう。
右辺と比較してみましょう。
右辺は磁場\(\boldsymbol{B}\)の時間微分です。磁場\(\boldsymbol{B}\)は単位面積当たりの磁束の時間微分なので以下の関係にあります。
両辺の分母を消去すると、
となります。積分形も左辺は領域の非線対称成分、右辺は領域内の時間微分であるので、微分形と積分形は同じ意味といえます。
1.3.4 微分形と積分形の右辺は同じ？
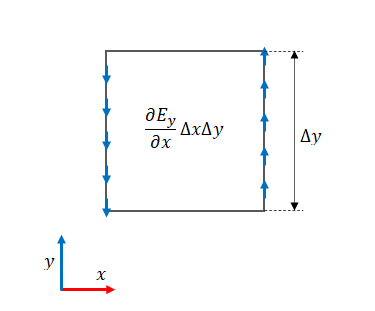
積分形の右辺は単位法線ベクトルと\(\boldsymbol{B}\)の時間微分の内積を面積分しています。
つまり、面の垂直成分のみが積分されます。
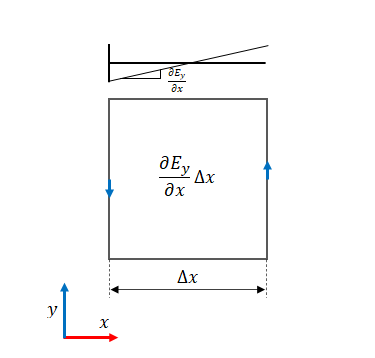
微分形は、上の図の1区画を切り取った状態を考えていました。
しかし微分形では法線ベクトルとの内積はありません。このままでは\(\boldsymbol{B}\)の時間微分の垂直成分だけが抽出されるわけではありません。積分形と等しいといえるのでしょうか。
これは次のように考えることができます。
微分形の左辺には回転があります。回転は対象の面に垂直な方向を向きます。したがって次のような面の向きでなければ成立しません。しかしこれでは積分形の面と向きが異なります。
そこで、ベクトルを垂直な2方向に分解します。
この上向きの成分のみを考慮すれば、積分形と向きが合います。
積分形では垂直方向の成分のみでしたが、微分形も垂直方向の成分のみになります。
上の図の横方向の成分は上方向と垂直であるため、互いに回転には影響を与えません。
1.4 磁場の変化があるところから離れた場所に電場が発生することが微分形より示される？
「ガウスの法則」の4.3節では電荷から離れた場所に電場が存在することが、ガウスの法則の微分形から示されることについて説明しました。同じようなことをマクスウェル – ファラデーの式についても考えてみます。
さて、微分形の左辺は回転で表します。回転の定義からわかるように回転は1点の状態のみを表します。周囲がどのような状態であっても値は変わりません。
ある点の磁場の変化が離れたところで電場として反映されるでしょうか。
微小な正方形で考えてみましょう。
画面手前から奥に向く磁場があり時間経過とともに大きくなっているとします。電場は反時計回りに生じます。
隣の正方形には常に磁場はありません。
隣の正方形の回転の大きさは0です。しかしこのままでは右辺に下向きの成分があるので回転があることになります。したがってこれを相殺するように、対する辺に同じ方向・大きさの電場があるはずです。
同じようにさらに隣の正方形も左側の辺に電場が生じます。
微分形の左辺は回転で表されます。回転は対象とする点のみにおける非線対称成分を表します。しかし、微分形は磁場の変化のあった点から離れたところでも電場が生じることを示しています。
1.5 積分形は任意の面で成立する？
ここまで、積分形は平面のみで成立するかのように述べてきましたがそのようなことはありません。曲面でも成立します。そのことを確認するために、境界が同じで異なる曲面の場合に右辺の積分が同一であることを確認しましょう。
次のようにボウル状の曲面\(S_1\)があり、その境界を\(C\)とします。\(S_1\)を磁場\(\boldsymbol{B}\)が貫いています。
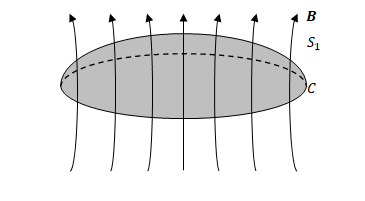
\(S_1\)を貫く磁束は以下で表されます。
$$ \int_{S_1} \boldsymbol{B} \cdot d\boldsymbol {S}$$
同じ様に曲面\(S_2\)についても磁束を求めます。ただし、境界は同じく\(C\)です。
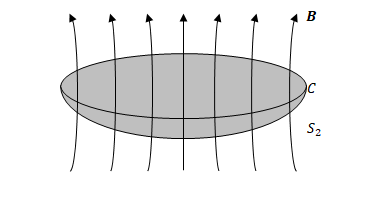
$$\int_{S_2} \boldsymbol{B} \cdot d\boldsymbol {S}$$
両者を合わせます。立体を\(V\)、立体の境界（表面）を\(S\)とします。\(S_2\)で求めた式は符号が反転します。
$$ \int_{S_1} \boldsymbol{B} \cdot d\boldsymbol {S} – \int_{S_2} \boldsymbol{B} \cdot d\boldsymbol {S} = \int_{S} \boldsymbol{B} \cdot d\boldsymbol {S}$$
ここで磁場に関するガウスの法則を適用します。
$$ \int_{S} \boldsymbol{B} \cdot d\boldsymbol {S} = \int_{V} \nabla \cdot \boldsymbol{B} dV = 0$$
したがって、
$$ \int_{S_1} \boldsymbol{B} \cdot d\boldsymbol {S} = \int_{S_2} \boldsymbol{B} \cdot d\boldsymbol {S} $$
となり、境界が同じであればいずれの曲面であっても貫く磁束が同じであることがわかります。
積分形の右辺はこの時間微分なのでこれも等しいといえます。
$$ – \frac {d} {dt} \int_{S_1} \boldsymbol{B} \cdot d\boldsymbol {S} = -\frac {d} {dt} \int_{S_2} \boldsymbol{B} \cdot d\boldsymbol {S} $$
つまり、曲面であっても積分形は成立します。
2 ファラデーの電磁誘導の法則
1章では、ファラデーが発見した法則をマクスウェルが記述した式（マクスウェル – ファラデーの式）について説明しました。この式は「ファラデーの電磁誘導の法則」を全て含むわけではありません。本章ではファラデーの電磁誘導の法則固有の部分を含め説明します。
用語や疑問に感じやすい点については3章に補足としてまとめました。
2.1 ファラデーの電磁誘導の法則
閉回路（回路：導線によって構成された、電流が流れる経路）を貫く磁束が変化すると閉回路に電圧が生じます。これを誘導起電力（起電力）とよびます（電圧・起電力などについては3.1節を参照ください）。
この磁束を\(\Phi\)、起電力を\(V_{emf}\)（emfはelectromotive forceの略）とすると、以下の関係にあります。
$$V_{emf} = -\frac {\partial \Phi} {\partial t} $$
この「回路を貫く磁束の変化」には2通りの場合があります。これらについて2.2、2.3節で説明します。
2.2 時間経過とともに磁束が変化する場合
まず、時間によって磁束が変化する場合を考えてみます。閉回路は変化しません。
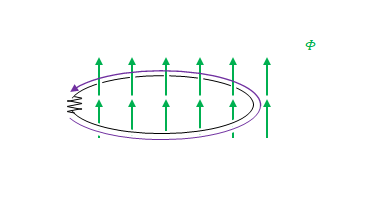
図のように閉回路がありその中を磁束\(\Phi\)が貫いているとします。左のジグザグの記号は抵抗です。
\(\Phi\)が小さくなりました。\(\displaystyle \frac{\partial \Phi} {\partial t}\)は下向きですが式の右辺はマイナスの符号がつくので上向きを正とすると右辺は正です。
\(V_{emf}\)は右辺が正の場合、右ねじの方向に発生します。したがって図の紫色が\(V_{emf}\)です。
2.3 時間経過とともに閉回路が変化する場合
次に、時間により閉回路が変化する場合です。
下の図のように閉回路の面積が小さくなったとします。
\(\Phi\)は小さくなるので\(V_{emf}\)はやはり正の方向、つまり図の方向に発生します。
2.4 マクスウェル – ファラデーの式とファラデーの電磁誘導の法則の違い
マクスウェル – ファラデーの式とファラデーの電磁誘導の法則は何が違うのでしょう。
改めて、マクスウェル – ファラデーの式とファラデーの電磁誘導の法則です。
マクスウェル – ファラデーの式（微分形）
$$ \nabla \times \boldsymbol{E} = – \frac {\partial \boldsymbol {B}} {\partial t} $$
マクスウェル – ファラデーの式（積分形）
$$ \oint_l \boldsymbol{E} \cdot d\boldsymbol {l} = -\frac {d}{dt} \int_S \boldsymbol{B}\cdot d\boldsymbol{S}$$
ファラデーの電磁誘導の法則
$$V_{emf} = -\frac {\partial \Phi} {\partial t} $$
さて、マクスウェル – ファラデーの式（積分形）の左辺は電場の線積分です（3.2節参照）。つまりこれが起電力といえそうです。式で表すと、
$$ \oint_l \boldsymbol{E} \cdot d\boldsymbol {l} = V_{emf} $$
です。
右辺はどうでしょう。
\(\boldsymbol{B}\)を面積分すると\(\Phi\)です。つまり、
$$ -\frac {d}{dt} \int_S \boldsymbol{B}\cdot d\boldsymbol{S} = -\frac {\partial \Phi} {\partial t}$$
です。
マクスウェル – ファラデーの式とファラデーの電磁誘導の法則が等しいことが容易に確認できたように思えます。しかし、常にこの関係が成立するわけではありません。
マクスウェル – ファラデーの式の微分形と積分形が等しいことを確認するときのことを思い出してください。微分形の両辺を面積分しましたね。
そして左辺はストークスの定理により面積分を境界の線積分に変換しました。
右辺は時間微分と面積分の順序を入れ替えただけです。
しかし、常に時間微分と面積分の順序を入れ替えることはできるわけではありません。
2.2節のような「時間経過とともに磁束だけが変化する場合」であれば入れ替えることができます。
2.3節のような「時間経過とともに閉回路が変化する場合」は入れ替えることができません。
磁束が存在し（大きさが0ではなく）、時間経過とともに変化しない場合を考えてみてください。マクスウェル – ファラデーの式の微分形では両辺の大きさは0です。しかしファラデーの電磁誘導の法則では起電力が発生します。
つまり、マクスウェル – ファラデーの式は「時間経過とともに磁束だけが変化する場合」のみに適用されます。
1.3節でストークスの定理を使って微分形と積分形が等しいことを確認しました。微分形の両辺を面積分し、右辺は時間微分と面積分を入れ替えました。しかしこれは時間経過とともに領域が変化しないという条件がないと成立しません。
2.5 時間経過とともに閉回路が変化する場合の例
前節の通り、ファラデーの電磁誘導の法則は「時間経過とともに磁束が変化する場合」と「閉回路が変化する場合」の2種類の異なる現象に適用されます。前者はマクスウェル – ファラデーの法則と同一であることがわかりました。後者はローレンツ力によって説明が可能です。
以下の例を考えましょう。物理でよく出題される問題と同じ構成です。
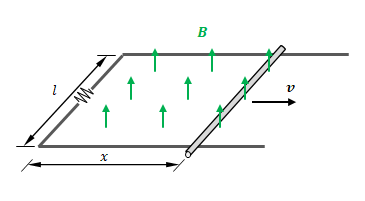
図の灰色の線は固定の導体です。右の丸い棒も導体で、固定の導体上を動かすことができます。左には抵抗があります。抵抗、固定の導体、丸棒で閉回路が形成されています。回路の内外に一様で時間経過とともに変化しない上向きの磁場\(\boldsymbol{B}\)があります。
丸棒を右に向かって速度\(\boldsymbol{v}\)で動かします。
ローレンツ力は以下の式で表されます。
$$\boldsymbol{F} =q(\boldsymbol{E} + \boldsymbol{v} \times \boldsymbol{B} ) $$
\(\boldsymbol{E}\)はないものとすると、
$$\boldsymbol{F} =q(\boldsymbol{v} \times \boldsymbol{B} ) $$
となります。\(\boldsymbol{F}\)が図の向きに生じます。
この力が導体内の電荷を動かす力、つまり起電力となります。力と起電力（Gを基準としたHの電位）の関係を求めましょう。
そのためにエネルギーを2通りの方法で求めます。
まず、電荷をHからGまで運ぶエネルギーは力と距離の積で表されます。1[N]の力で1[m]動かすには1[J]（ジュール）のエネルギーが必要です。
$$U=Fl$$
また、電圧と電荷の積もエネルギーです。1[C]の電荷を1[V]の電位差のある2点間を運ぶには1[J]のエネルギーが必要です。Gを基準とするとHの電位は負なので、
$$U=-qV$$
両者より、
$$V=-\frac{Fl}{q}=-\frac{qvBl}{q}=-vBl$$
となります。
$$v=\frac{d x}{d t}$$
より、
$$V=-\frac{d x}{d t} B l$$
$$\Phi=SB=xlB$$
なので、
$$V=-\frac{\partial \Phi}{\partial t}$$
以上、時間経過とともに閉回路が変化する場合について、ファラデーの電磁誘導の法則の通りになることが確認できました。
※一般的には電位と速度・磁場・長さの関係は\(V=vBl\)とされ負号はつきませんが、これは大きさの関係を示しているからと思われます。ここでは上からみて基準点から反時計回りに進んだ点の電位として符号を決めています。
3 前章の補足
3.1 電圧・電位・電位差・起電力
電圧・電位・起電力の単位は同じでいずれもV（ボルト）です。
電圧と電位は基準となる点があるかどうかの違いです。
電圧は任意の2点の間の値です。
電位は任意の1点と基準点の間の値です。
同じように思えますが、複数の値を表す場合、意味が異なります。
電圧はそれぞれの値について2点が示されなければなりません。
電位の場合は、1点を基準とすることにより、それぞれの値について1点のみが示されればよいことになります。グラウンドやアースという言葉を聞いたことがあるかもしれませんが、回路設計においてはこれらが暗黙の了解で基準の電位とされることがあります。
電位差は2点の電位の差のことで、電圧とほぼ同じ意味です。
上記両者は1点を基準とするかしないかの違いでしたが、起電力は発生の仕方に関する定義です。電磁誘導や化学などの作用によって生じた電圧または電位を起電力とよびます。特に電磁誘導による起電力を誘導起電力とよびます。語の中に「電力」とありますがW（ワット）が単位ではありません。電流を流す力という意味です。
3.2 電場と電位の関係
高校で物理を選択した方はコンデンサの内部における電場と電位の関係を教わったと思います。電極間の距離を\(d\)とすると、
$$E=\frac{V}{d}$$
ですね。
電場が一様な場合であればこれでよいのですが、一様でない場合はこの通りではありません。2点間を細かく分割して考えれば微分で表わされることがわかります。さらに、3次元の空間であればそれぞれの方向に関する微分を足せばよいはずです。電場は電圧の高いほうの向きを正とします。以上より、
$$\boldsymbol{E}=- \nabla V$$
と表されます。\(\nabla\)はベクトル場における勾配です。勾配については、よろしければ「スカラー場の勾配」をご覧ください。
積分を使って表すこともできます。両辺を積分すると、点Aを基準とした点Bの電位は
$$V=\int_B^A \boldsymbol{E} \cdot d \boldsymbol{l}$$
と表されます。右辺は線積分ですが、経路には依存しません。
山の2点間の経路について考えてみましょう。点Aから点Bに向かう複数の経路があるとします。両者の高低差が電圧、各箇所での勾配が電場です。
経路によって標高でも経路によって勾配は異なりますが、始点と終点であれば高低差は同じです。電場と電位の関係も同じで、線積分の経路には依存しません。正確な証明は省略します。
ただし、2.3節、2.4節のようにローレンツ力により電位が変化する場合はこの関係が成立するわけではありません。
3.3 導体に起電力が発生する？
図において電源の電圧を\(V\)、電流を\(I\)、抵抗を\(R\)とすると、
$$V=IR$$
ですね。この\(R\)がない場合はどうなるでしょう。
\(R\)が0なので、\(V\)が一定であれば\(I\)は無限大ということになります。いわゆるショートという状態です。発煙や発火の原因となるのは大きな電流が流れるからです。
では電磁誘導が発生した状態について考えてみましょう。左の抵抗の両端に起電力が発生しています。抵抗は導線に接続されています。導線の抵抗が0にもかかわらず起電力が発生するのでしょうか。
電磁誘導は過渡的な現象で、\(V=IR\)が常に成立するわけではありません。この場合、自己インダクタンス\(L\)を用いて
$$V=L\frac{dI} {dt}$$
と表されます。つまり導体であっても2点間に起電力が発生します。
※電源をショートさせると火災の原因になるので決して試さないでください。
3.4 全て導体で構成された閉回路の場合、どこに起電力が発生する？
前節の通り、磁場が変化したところまたは回路を動かしたところの導線に起電力が発生します。ある点を基準として導線をたどると徐々に電位は上昇（または下降）していきます。
もし回路が全て導線で構成されていた場合（抵抗がない場合）1周回って元の位置にたどり着いたとき、その点の電位はどうなるのでしょう。始点と終点では回路全体に生じる電位差がなければならないのに、両者が接続されていると電位差が生じないはずです。
前節の図のように抵抗があれば、両端の電圧に比例して電流が流れ、電流との積が起電力と一致します。つまり、起電力で上がった分が抵抗で下がるのでどの点でも矛盾はありません。
では抵抗がない場合はどうなのでしょう。
前節の直流電源がショートした状態の図を思い出してください。理論上は無限大の電流が流れます。実際には電源がショートを検出して停止します。もしこの機能がはたらかなかった場合、直流電源が流せる電流には上限があり、上限近くになると電圧が低下します。一方で導線も0[Ω]ではありません。わずかに抵抗値があります。電圧が電流と抵抗値の積になるまで低下し安定します。
電磁誘導の場合も直流電源と同じようにショートの状態になります。実際には導線上にはわずかに抵抗値があります。抵抗に電流が流れると発熱します。このエネルギーは棒を動かすエネルギーと同じ大きさです。したがってわずかに発熱する程度です。
※電源をショートさせると火災の原因になるので決して試さないでください。
3.5 磁石とコイルを使った例
ここまで、物理量の作用をみてきましたが、実際の例として棒磁石を使った場合とコイルと使った場合について考えてみましょう。
図は棒磁石と巻き数1の閉回路がある状態です。N極よりS極に向けて磁束線が出ています。
棒磁石を閉回路に向けて近づけました。
閉回路内の磁束線を比較してください。増えていますね。磁束が増えた状態です。磁束線が密なところは磁束密度（磁場）が大きく、疎なところは磁束密度が小さいと考えてください。つまり棒磁石を閉回路に近づけるということは磁束が大きくなります。
次にコイルについて考えてみましょう。
導線の磁石からの距離の差が無視できるほど密に巻かれている場合、その回数分だけ起電力は重畳されると考えることができます。したがってコイルの巻き数をNとすると、ファラデーの電磁誘導の法則は、
$$V_{emf} = -N \frac{d \Phi} {d t}$$
となります。
3.6 レンツの法則
レンツの法則は「誘導電流は、その原因を妨げる向きに発生する」というものです。
あるいは「誘導電流は、磁束の変化を妨げる向きに発生する」とされる場合もあります。
いずれの記述であっても時間経過とともに磁束が変化する場合が該当します。
下の図は磁束が変化する前です。
磁束が小さくなりました。紫色の方向に電流が流れます。このとき、赤色の向きに磁束が発生します。図では1か所に小さく描いていますが、回路全体で同様の向きに磁束が発生します。また、導線の近くだけではなく、導線で囲われた領域内全体で発生します。これは磁束の減少を妨げようとする方向です。レンツの法則の通りです。磁束を変化させるためには誘導電流により生じる磁束に逆らう必要があり磁気エネルギーが必要となります。
冒頭でレンツの法則について2通り述べましたが、後者は2.3節のように時間経過とともに閉回路が変化する場合は適用されません。前者であれば適用されます。この場合は以下のような作用があります。
丸棒を右に動かすと起電力はHを基準としてGが正となります。電流はこの向きに流れます（図の青色）。フレミングの左手の法則により左向きに力が発生します（図の赤色）。
この力はローレンツ力とは異なります。丸棒を動かすとローレンツ力により電荷が動きます。この電荷の動きが電流です。電流が流れることにより丸棒を動かす力が発生します。
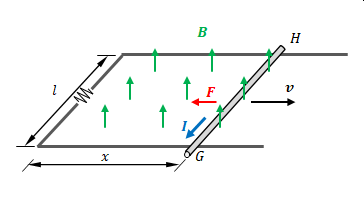
丸棒を右方向に動かそうとすると逆方向、つまり電磁誘導を抑制する方向に力がかかります。
この力に逆らって丸棒を動かす運動エネルギーが回路上で電気エネルギーとなり、抵抗で発熱し熱エネルギーに変わります。理論上は3者は等しい値です。
いずれの場合もただではエネルギーは得られないということを示していますね。
一例ですが、コイルを縦にして中を通るように上から棒磁石を自由落下させるとその速度は変化するでしょうか。
コイルがない場合に比べて落下速度は小さくなります。電磁誘導によって電気エネルギーが発生する分、運動エネルギーが減少すると考えることができます。
レンツの法則は誘導電流の発生する向きを示しているだけで、それ以外のことには言及していません。ファラデーの電磁誘導の法則では右辺に負号がつきましたが、これはレンツの法則に合致しています。その意味ではレンツの法則はファラデーの電磁誘導の法則に包含されるといえます。
4 まとめ
・本ページでは以下のように区別しました。
マクスウェル – ファラデーの式：
時間経過とともに磁場（磁束）が変化した場合
ファラデーの電磁誘導の法則：
時間経過とともに磁束（磁場）が変化した場合、閉回路が変化した場合
マクスウェルの方程式の一つとして記述されているのは前者です。
・ファラデーの電磁誘導の法則は以下です。
$$V_{emf} = -\frac {\partial \Phi} {\partial t} $$
・電場を線積分することにより電位が得られます。したがってマクスウェル – ファラデーの式（積分形）の左辺は電位に変換できます。右辺は磁場の面積分を磁束に置き換えることにより磁束の時間微分になります。したがって時間経過とともに磁束のみ変化した場合はマクスウェル – ファラデーの式とファラデーの電磁誘導の法則は同じであるといえます。
・時間経過とともに閉回路が変化する場合、微分の両辺を線積分した後に、右辺は時間微分と線積分を入れ替えられません。したがってマクスウェル – ファラデーの式とファラデーの電磁誘導の法則は同じとはいえません。
・閉回路の変化によって電位差が発生するのはローレンツ力によるものです。
・ストークスの定理によりマクスウェル – ファラデーの式の微分形と積分形が同じであることが確認できます。