物理学・工学では、空間に分布する物理量をベクトル場やスカラー場で表すことがあります。これらは通常、多変数関数として表すため、空間の変化の度合いを示すには1変数関数の微分とは異なる演算(作用)が必要です。その一つが勾配です(発散と回転もありますが、次ページ以降で説明します)。
本ページではベクトル場・スカラー場と多変数関数の微分に関する説明の後、勾配について述べます。
1 ベクトル場・スカラー場
1.1 ベクトル場
ベクトル場とは、全ての点においてベクトルが割り当てられている空間のことです。
例えば、ある点で風の向きと大きさを測定したとします。これはベクトルで表すことができます。しかし単一のベクトルは通常、ベクトル場とはよびません。
実際には空間のいたるところで風が存在します。計算などによって全ての箇所の風をベクトルで表した場合、その空間はベクトル場です。下の図では飛び飛びにベクトルが存在するように描いていますが、描画している点と点の間には無数のベクトルが存在すると考えてください。
ベクトル場は3次元だけではなく、どの次元であっても定義することができます。

1.2 スカラー場
スカラー場とは、全ての点においてスカラーの値が割り当てられている空間のことです。
ある点の気温を測定したとします。これはスカラーです。しかしこれだけでは通常スカラー場ではありません。
計算などによって空間の全ての点について気温で表すことができたとします。その場合、その空間はスカラー場です。
下の図は気温を色で表したものです。3次元のスカラー場は、画面上、値を長さで表すことが難しいのでここでは色で表現しています。代表して等間隔にある点のみの気温を表していると考えてください。
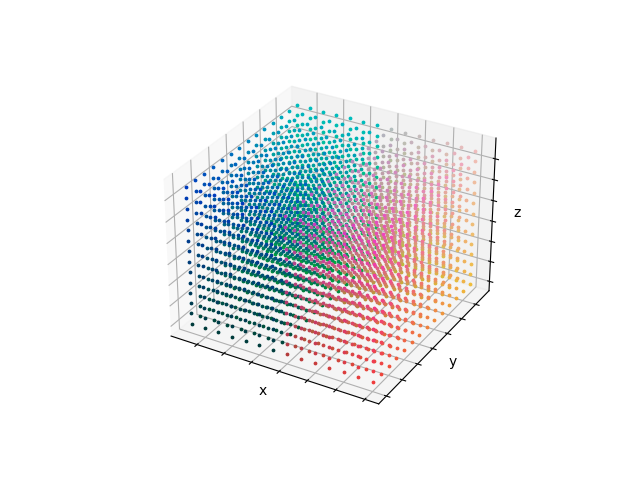
スカラー場はどの次元であっても定義することができます。
下の図のように面で表現される場合、場は3次元ではなく2次元である点に注意してください。水平の2方向が空間で、縦方向はスカラーの値を示しています。
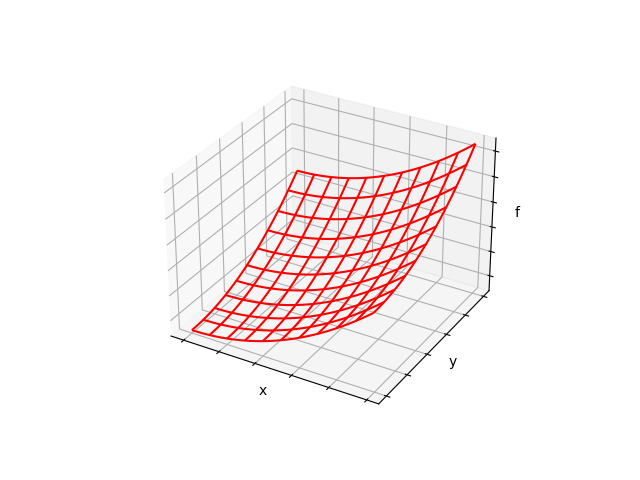
1.3 ベクトル値関数・スカラー値関数
値がベクトルである関数のことをベクトル値関数(ベクトル関数)とよびます。下記のように、ベクトルと同様、通常は太字で表します。
$$\boldsymbol{f}(x)$$
スカラーの値をもつ関数はスカラー値関数(スカラー関数)とよびます。下記のように表します。
$$f(x)$$
関数に入力する変数はベクトル・スカラーどちらも可能です。
空間の座標を変数としてベクトル値関数・スカラー値関数を記述した場合、それらはベクトル場・スカラー場を表しています。
2 微分
2.1 偏微分
偏微分とはスカラー値またはベクトル値の多変数関数(例:\(f(x,y)\)、\(\boldsymbol{f}(x,y)\))を一つの変数について微分する演算(作用)です。その他の変数については何の作用もなく、定数のように扱われます。
表記はいろいろありますが、その一つが以下です。
$$\frac {\partial {f(x, y)}} {\partial {x}} $$
例えば\(f(x,y)=x^2y^3\)とすると、\(x\)の偏微分は以下です。
$$\frac {\partial {f(x, y)}} {\partial {x}} = 2 x 3y^3$$
偏微分とは別に「全微分」というものもありますが、ここでは省略します。
偏微分というと難しい印象がありますが、この通り1変数関数における微分とほとんど同じです。偏微分方程式は確一般的に難解です。しかし偏微分自体は難しくないと思います。
2.2 \(\nabla\)(ナブラまたはデル)
\(\nabla\)とはスカラー場・ベクトル場の空間微分を記述するための演算子(作用素)です。
\(x\)、\(y\)、\(z\)方向の単位ベクトルをそれぞれ \(\boldsymbol{i}\)、 \(\boldsymbol{j}\)、 \(\boldsymbol{k}\)とすると以下のように表すことができます。
$$\nabla = \frac {\partial } {\partial {x}} \boldsymbol{i} + \frac {\partial } {\partial {y}} \boldsymbol{j} + \frac {\partial } {\partial {z}} \boldsymbol{k} $$
括弧を使って以下のように表すこともできます。
$$\nabla = ( \frac {\partial } {\partial {x}} , \frac {\partial } {\partial {y}} , \frac {\partial } {\partial {z}} )$$
なかなかこの演算子には慣れないかもしれませんが、3次元であれば3つ必要となる式を一つで表現でき便利です。
\(\nabla\) 自体が値をもつわけではありません。\(\nabla\)の後に続くスカラー値関数またはベクトル値関数との組み合わせによって値をもちます。
組み合わせによって演算(作用)も異なります。例えば後述の勾配や次ページ以降で説明する発散・回転でも\(\nabla\)を使いますがいずれも異なる演算です。
3 勾配
3.1 概要
勾配(グラディエント)とはスカラー場を傾きをベクトルで表す演算(作用)です。
傾きであるなら微分(偏微分)と同じではないでしょうか。
似ていますが、微分(偏微分)は傾きをスカラー値で表すのに対し、勾配はベクトルで表します。
向きはそれぞれの座標軸の正の方向です。
3.2 定義
3次元の場合の定義は式で表す場合は以下です。
$$\nabla f = \frac {\partial {f}} {\partial {x}} \boldsymbol{i}+ \frac {\partial {f}} {\partial {y}} \boldsymbol{j} + \frac {\partial {f}} {\partial {z}} \boldsymbol{k} $$
\(f\)はスカラーです。 \(\boldsymbol{i}\)、 \(\boldsymbol{j}\)、 \(\boldsymbol{k}\)はそれぞれ\(x\)方向、\(y\)方向、\(z\)方向の単位ベクトルです。
括弧を使って以下のように表すこともできます。
$$ ( \frac {\partial {f}} {\partial {x}} , \frac {\partial {f}} {\partial {x}} , \frac {\partial {f}} {\partial {x}} ) $$
\(\nabla\)を使わず以下のように表すこともあります。
$$\boldsymbol{grad} \boldsymbol{f}$$
gradはgradientの短縮形です。
3.3 定義の意味
3次元はイメージしづらいので2次元で考えてみましょう。2次元の場合、式は以下です。
$$\nabla = \frac {\partial } {\partial {x}} \boldsymbol{i} + \frac {\partial } {\partial {y}} \boldsymbol{j} $$
水平方向が\(x\)と\(y\)、垂直方向が\(f\)です。\(f\)は図のような曲面であったとします。
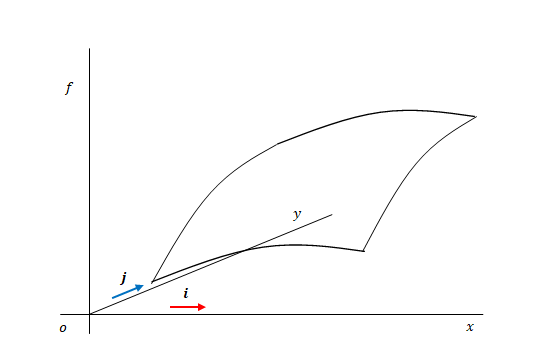
曲面のある点に接する微小領域に注目します。これは平面かつ長方形であると考えてください。微小領域であるため、曲面との誤差は無視します。
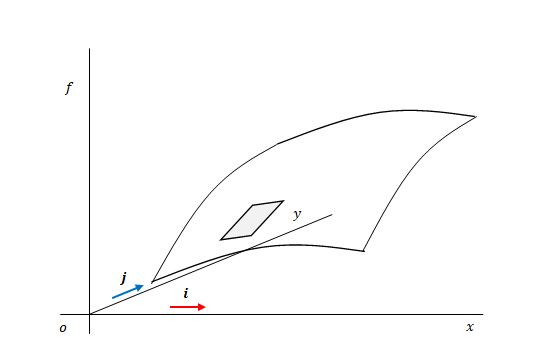
拡大します。
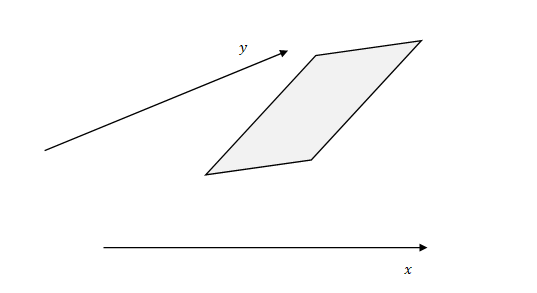
微小領域の\(x\)方向の境界(線)に注目します。
この線の傾きはどれだけでしょう。
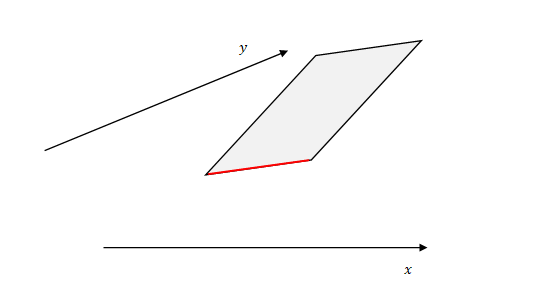
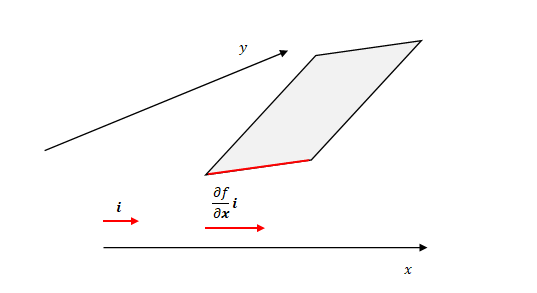
この線上では\(y\)は変化していません。したがって傾きは\(x\)についての偏微分です。
傾き単位ベクトルを追加しベクトルにすると、\(\frac {\partial {f}} {\partial {x}} \boldsymbol{i}\)です。
同じように\(y\)方向についても傾きに単位ベクトルを掛けると \(\frac {\partial {f}} {\partial {y}} \boldsymbol{j}\)となります。
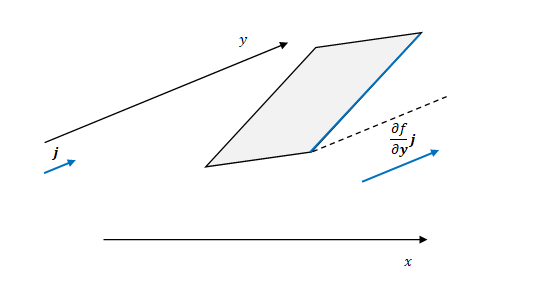
勾配は今求めた二つのベクトルの和です。つまり図の紫のベクトルです。
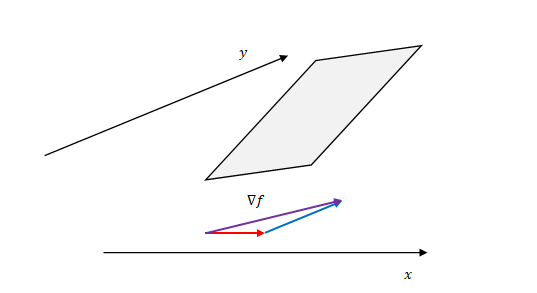
このグラフ上では勾配は水平方向のベクトルとして定義される点に注意してください。垂直方向の成分はありません。
3.4 勾配の例
下の図の赤は\(f\)(2次元)、青はその勾配を示しています。\(f\)は\(x\)、\(y\)の2次の項を含んでいます。勾配は\(x\)と\(y\)それぞれについて1次関数になります。つまり増分は一定です。
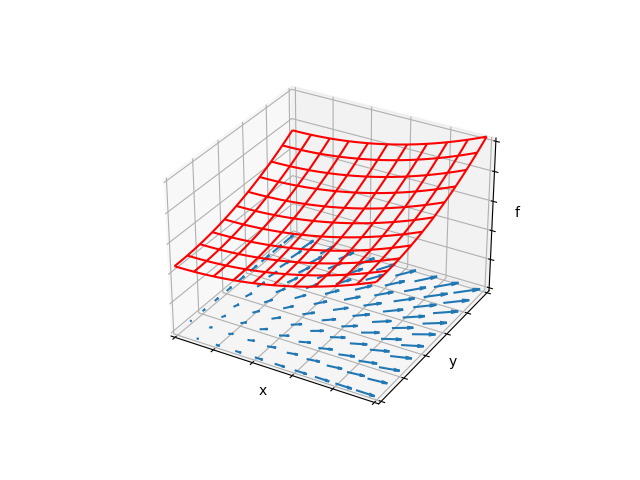
もう一つ例です。fは\(x\)の三角関数と\(y\)の2次関数を含みます。
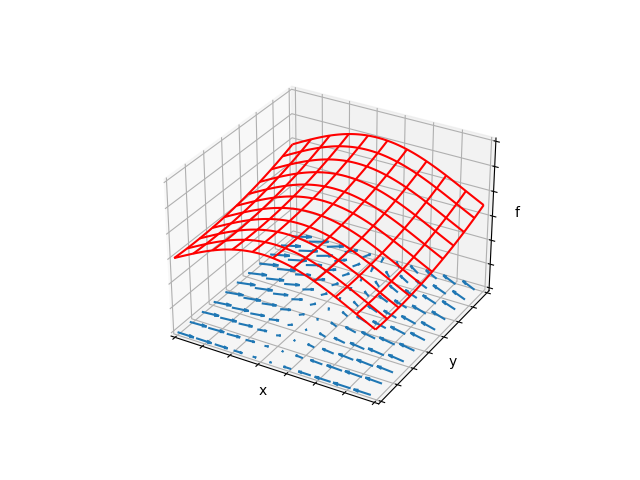
4 まとめ
4.1 ベクトル場・スカラー場
ベクトル場とは全ての点にベクトルが割り当てられている空間のことです。
スカラー場とは全ての点にスカラー場が割り当てられている空間のことです。
4.2 偏微分
偏微分とは多変数関数における微分の一種で、一つの変数についての微分する演算です。その他の変数については何の作用もなく、定数のように扱われます。
4.3 \(\nabla\)
\(\nabla\)とはスカラー場・ベクトル場の空間微分を記述するための演算子です(下記)。
$$\nabla = \frac {\partial } {\partial {x}} \boldsymbol{i} + \frac {\partial } {\partial {y}} \boldsymbol{j} + \frac {\partial } {\partial {z}} \boldsymbol{k} $$
または
$$\nabla = \left( \frac {\partial } {\partial {x}} , \frac {\partial } {\partial {y}} , \frac {\partial } {\partial {z}} \right)$$
4.4 勾配
勾配とはスカラー場の傾きをベクトルで表す演算です(下記)。
$$\nabla f = \frac {\partial {f}} {\partial {x}} \boldsymbol{i}+ \frac {\partial {f}} {\partial {y}} \boldsymbol{j} + \frac {\partial {f}} {\partial {z}} \boldsymbol{k} $$
または
$$ \left( \frac {\partial {f}} {\partial {x}} , \frac {\partial {f}} {\partial {x}} , \frac {\partial {f}} {\partial {x}} \right) $$
