減衰振動

外部からの強制的な力がなくても振動をしたり、均衡が保たれた状態に収束する物理現象があります。例えばバネを引っ張って離すと振動しながら減衰します。

このような現象は三角関数と指数関数で表されます。条件によっては指数関数のみが出てくる場合もあります。これらを合わせ、なぜそうなるのかを考えてみましょう。

※ 微分の記法は1種類ではありません（ライプニッツの記法、ラグランジュの記法、ニュートンの記号など）。使う記法は分野によって異なります。本ページではそれぞれの分野で一般的に使われる記法に合わせています。

1 バネの例

※以下、微分はライプニッツの記法です。

(1)バネの運動を式で表す

中学校の理科の時間を思い出しましょう。バネを伸ばしたり縮めたりするとその力に比例して伸びたり縮んだりしましたね。

ばねにおもりをつけて水平な台に置いたとします。おもりと台の間の摩擦はありません。

おもりの横方向の位置（変位）を\(x\)とします。外部より力を加えない状態で静止しているときの変位が\(x=0\)です。

おもりを引っ張って手を離しました。このときのばねを引っ張る力（弾性力）を\(F_e(t)\)、ばね定数を\(\omega^2\)とします。ばね定数を二乗にしているのは後で式の変形をしやすくするためです。

$$F_e(t)=ｰ\omega^2 x(t)$$

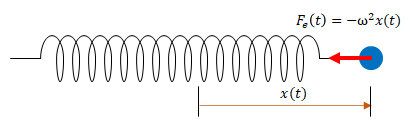
おもりの加速度を\(\alpha(t)\)、質量を\(m\)とすると以下の関係にあります。

$$F_k(t)=m \alpha(t) $$

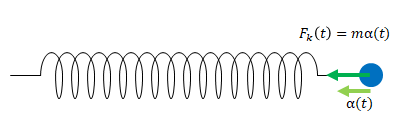
さらに、おもりが受ける空気抵抗の影響（粘性抵抗）を考えます。粘性抵抗は物体の速度に比例します。粘性抵抗を\(F_v(t)\)、速度\(v(t)\)、係数を\(2 \gamma v\)とします。係数に2がありますが、これも後で式を少し簡単にするためのものです。

$$F_v(t) = -2 \gamma v(t) $$

これらの力は以下の関係にあります。

$$F_k(t) + F_e(t) + F_v(t) = 0$$

前述の関係式を代入すると、

$$m \alpha(t) + 2 \gamma v(t) + \omega^2x(t) = 0$$

変位を時間で微分すると速度、速度を時間で微分すると加速度なので、

$$\alpha(t) = \frac {d^2 x(t)} {dt^2} $$

$$v(t) = \frac {d x(t)} {dt} $$

これを代入して、

$$\frac {d^2x(t)} {dt^2} + 2 \gamma \frac {dx(t)} {dt} + \omega ^2 x(t) = 0$$

この式を満たす\(x(t)\)（解）がおもりの運動を示していることになります。

\(\gamma\)が0であればおもりの運動は高校の物理の時間に教わった「単振動」ですが、粘性抵抗を考慮すると\(\gamma\)と\(\omega\)の関係によって単振動とは異なる動きをします。

解を求め、おもりがどのような運動をするかを考えます。

2 微分方程式

※以下、微分はラグランジュの記法です。

(1)微分方程式とは

前項の最後に示した式は微分方程式です。微分方程式とは、ある関数と、微分をした関数を含む方程式です。通常、解は値ではなく、関数です。

微分方程式には普遍的な解法があるわけではなく（解法がない場合もあります）、式の構成によって区別されます。

例えばこの式は「2階線形斉次微分方程式」とよばれます。

$$ x” + 2 \gamma x’ + \omega ^2 x = 0$$

以下、簡単に言葉の説明をします。

・n階
式の中で最も高い導関数 ※1 の階数のことです。 階数とは何回微分をした関数であるかを示します。例えば\(x’\)は1階、\(x”\)は2階です。

・線形
項に含まれる未知の関数またはその微分した関数が1個以下である場合です。

この場合は全ての項に含まれる\(x”\)、\(x’\)、\(x\)は1個以下ですが、

$$x” + 2 \gamma x’ + \omega^2 x = 0$$

下の式は2個の項があるので非線形です。

$$x” + 2 \gamma x’x + \omega ^2 x = 0$$

\(\log x\)のような項があっても非線形です。

大した差ではないように思えますが一般的には非線形微分方程式には解法がありません。

・斉次 ※2
斉次微分方程式とは全ての項が未知関数またはその導関数または0である関数です。

例えば、この式は斉次微分方程式ですが、

$$x” + 2 \gamma x’ + \omega ^2 x = 0$$

下の式は非斉次方程式です。

$$x” + 2 \gamma x’ + \omega ^2 x = 1$$

※1 導関数とは微分をして得られる関数のことです。

※2「斉次」ではなく「同次」、「線形」ではなく「線型」と書くこともあります。用語の順序が異なる場合もあります。「変数係数」と区別するために「変数係数」を付ける場合もあります。

(2)1階斉次線形微分方程式の解法

求めたいのは2階斉次線形微分方程式ですが、その前に次のような1階斉次線形微分方程式を考えてみます。

$$x’ = x$$

解析的に解くこともできますが、解を予想してみましょう。

微分をして自分自身になる関数といえば何でしょう。

指数関数ですね。

\(e^x\)を微分しても\(e^x\)なのでこの方程式の解です。

以下の方程式の解は \(e^{2x}\)です。

$$x’ = 2x$$

後述しますが、2階線形斉次微分方程式も同様の方法で解を求めます。

(3)重ね合わせの原理

斉次線形微分方程式の解が\(x_1\)、\(x_2\)であったとします。この場合、以下も解になります。

$$ c_1 x_1 + c_2 x_2 $$

\(c_1\)、\(c_2\)は任意の定数です。

これを「重ね合わせの原理」とよびます。

なぜそうなるのかは「＋」のボタンを押して確認してください。

3 バネの運動の求め方

※以下、微分はニュートンの記法です。

1階斉次微分方程式の解は指数関数でした。2階斉次線形微分方程式についても同じように解を予想し、式が成立する係数を求めます。

解を\(e^{\lambda t}\)とします。\(\lambda\)は未知数です。

この式に\(x(t)=e^{\lambda t}\)を代入します。

$$\ddot{x} + 2 \gamma \dot{x} + \omega ^2 x = 0$$

$$\lambda ^2 e^{\lambda t} + 2 \gamma \lambda e^{\lambda t } + \omega ^2 e ^{\lambda t} = 0$$

\(e^{\lambda t}\)が各項共通なので、

$$(\lambda ^2 + 2 \gamma \lambda + \omega ^2 )e ^{\lambda t} = 0$$

となります。 \(e^{\lambda t}\) は0ではないので括弧の中が0（下記）であればよいことになります。

$$ \lambda ^2 + 2 \gamma \lambda + \omega ^2 =0$$

2階斉次線形微分方程式において \(e ^{\lambda t}\) を解とすると、上記のような方程式が得られます。未知数は\(\lambda\) です。この方程式を特性方程式とよびます。 解くと\(\lambda\)を\(\gamma\)と\(\omega\)で表すことができます。 そして\(x(t)=e^{\lambda t}\)に代入すれば\(x(t)\)の解が得られます。

特性方程式より、2次方程式の解の公式にあてはめると、

$$\lambda = \frac {- 2\gamma \pm \sqrt{ 4\gamma ^ 2 – 4\omega ^ 2} } {2} $$

約分して

$$\lambda = -\gamma \pm \sqrt {\gamma ^2 – \omega ^2} $$

となります。\(x(t)\)の式に代入すると、

$$x(t)=e^{ -\gamma \pm \sqrt {\gamma ^2 – \omega ^2}t } $$

重ね合わせの原理より、

$$x(t)=e^{-\gamma t} (c_1 e^{ \sqrt {\gamma ^2 – \omega ^2}t } + c_2 e^{ – \sqrt {\gamma ^2 – \omega ^2}t }) \quad (2)$$

ただし、これだけではおもりがどのような挙動をするのかイメージしづらいと思います。指数部の根号の中が正か負か0かによって異なります。

また、そもそもの解に例外もあります。

以下、\(\gamma\)と\(\omega\)の関係によって場合分けをして考えます。

\(\omega\)はバネの強さ、\(\gamma\)は粘性抵抗に関係がある定数であることを念頭に置いてください。

4 場合ごとのバネの運動

(1)\(\gamma = 0\)の場合

粘性抵抗が0の場合です。

式(2)で\(\gamma = 0 \)を代入すると、

$$x(t)=c_1 e^{i \omega t} + c_2 e^{-i \omega t}$$

指数部が虚数なのでオイラーの公式により三角関数で表すことができます。

詳細は省略しますが、\(x(0)=1\)（初期状態の変位が1）、\(\dot{x}(0)=0\)（初期状態の速度が0）を代入すると以下になります。

$$x(t)=\cos(\omega t)$$

虚数の項は消えて\(\cos\)のみになります。

おもりは単振動（不減衰振動）をします。つまり、おもりは永遠に振動を続けます。

(2)\(\gamma < \omega\)の場合

粘性抵抗が小さい場合です。

$$\omega_0 = \sqrt{ \omega^2 – \gamma^2 } $$

とすると式(2)は

$$x(t)=e ^ {\gamma t } (c_1 e^{ i \omega_0 t } + c_2 e^{ – i \omega_0 t })$$

\(x(0)=1\)、\(\dot{x}(0)=0\)を代入すると、

$$A e ^{-\gamma t} \cos(\omega_0 t + \alpha)$$

となります。\(A\)と\(\alpha\)は定数です。

前項では\(\gamma = 0\)だったので\(e^{-\gamma t}\)が定数となり式には現れませんでしたが、本項の場合は定数ではありません。\(t\)が大きくなる とともに \(e^{\gamma t}\)は小さくなります。

したがって\(x(t)\)は振動しながら減衰します（減衰振動）。

(3)\(\gamma > \omega\)の場合

粘性抵抗が大きい場合です。

$$\eta_0 = \sqrt {\gamma^2 – \omega^2} \quad (3)$$

とすると式(2)は

$$x(t)=e ^{-\gamma t} ( c_1 e^{ \eta_0 t } + c_2 e^{- \eta_0 t })$$

展開すると1項目はe^{(-\gamma + \eta_0) t }ですが、式(3)より

$$\gamma > \eta_0 $$

なので1項目の指数は負になり\(t\)の増加とともに減衰します。2項目の指数も負なので減衰します。

したがって\(x(t)\)は減衰します。

\(e\)の指数部が実数であることからわかるように、振動はしません。

この減衰を「過減衰」とよびます。必要以上に急速に収束するかのようなイメージがありますが、次に述べる「臨界減衰」に比べれば緩やかに減衰します。

バネの運動において減衰の原因となるのは粘性抵抗ですが、これが大きすぎると収束は遅れます。この減衰の原因が大きすぎるということなのでしょう。英語では「overdamped」とよびますが、「弱めすぎる」という意味です。これがイメージに近いでしょう。

(4)\(\gamma = \omega\)の場合

ここまで、解を$$x(t) = e^{\lambda t}$$と置いて特性方程式の解から\(e\)の指数を求めてきました。特性方程式は2次なので通常、解は2個あります。しかし\(\gamma = \omega\)の場合は根号の中が0になるので重解になります。その解は\(e^{- \gamma t }\)です。

しかし、それだけではありません。\(t e^{- \gamma t} \)も解です。\(e\)の前に\(t\)がついているところに注意してください。

重ね合わせの原理を適用すると、

$$x(t)=( c_1 + c_2 t )e ^{-\gamma t}$$

となります。

なぜそうなるかについては「＋」を押して展開して確認してください。

この減衰を「臨界減衰」とよびます。振動はありません。減衰は最も速くなります。

5 まとめ

(1)解法

・バネの弾性力、粘性抵抗より、微分関数を作ります。

・微分方程式の解を指数関数とします。指数関数の係数や指数部は未知です。

・微分方程式に代入し各項の指数関数の係数を集めた式が0になる解を求めます（特性方程式）。

・特性方程式の解を指数とする指数関数が求める解（おもりの変位）です。

(2)条件による挙動の違い

\(\bf{\large{ 条件 }}\)	\( \large{ x(t)}\)	\(\bf{\large{ 動作 }}\)
\(\large{\gamma = 0}\)	\(\large{\cos(\omega t)} \)	\(\bf{\large{単振動}}\)
\(\large{\gamma < \omega}\)	\( \large{A e ^{-\gamma t} \cos(\omega_0 t + \alpha) }\)	\(\bf{\large{ 減衰振動 }}\)
\(\large{\gamma > \omega}\)	\( \large {e ^{-\gamma t} ( c_1 e^{ \eta_0 t } + c_2 e^{- \eta_0 t }) } \)	\(\bf{\large{ 過減衰 }}\)
\(\large{\gamma = \omega}\)	\( \large{( c_1 + c_2 t )e ^{-\gamma t}}\)	\(\bf{\large{ 臨界減衰 }}\)

(3)\(\gamma\)と\(x(t)\)の波形の対応

以下は\(\omega\)を固定とし、\(\gamma\)を変化させながら\(x(t)\)を表示した図です。

時間経過とともに波形が変わるということではありません。\(\gamma\)と\(\omega\)の関係によって\(x(t)\)がどう変わるかを視覚的に表すことが目的です。

\(\gamma\)は0から開始し少しずつ増やしています。途中、1秒弱止まるところがありますが、これが臨界減衰です。

(4)なぜ減衰振動は指数関数と三角関数で表される？

余談ですが、なぜ減衰振動は指数関数と三角関数で表されるのでしょう。

原因をたどっていくと、ばねの運動を線形微分方程式で表すことができるから、と考えることができます。

線形微分方程式には変位の時間関数とその導関数が含まれます。関数に定数を掛けただけで一致しなければなりません。指数関数であれば指数・係数次第では導関数が同じになります。場合によっては三角関数も同様です。したがって、これらが解に現れたのでした。

本ページではばねの運動を取り上げましたが、似たような微分方程式で表すことのできる物理現象は数多く存在します。物理学・工学において指数関数や三角関数が頻繁に出てくるのはそのような理由があります。

また、主に工学では過渡現象を解析するためにラプラス変換を使うことがあります。ラプラス変換が使われるのは、指数関数を簡単な形式で表すことができ都合がよいからでしょう。