前ページではスカラー場の勾配について説明しましたが、ここではベクトル場の発散について述べます。
1 発散が正になる場合、負になる場合
発散とはベクトル場の流出(湧き出し)、流入(吸い込み)をスカラー場で表現する演算です。
点ごとに流出を正、流入を負としてその総量で表します。
場合に分けて発散の値がどうなるかを2次元のベクトル場について考えてみましょう。
点から全方向にベクトルが向いている場合、発散は正です。

全方向から点にベクトルが向いている場合、発散は負です。
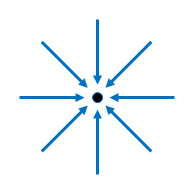
点にから外に向いているベクトルと点に向いているベクトルがある場合はその量の差です。この図の場合は正です。

点に向いている、あるいは点から外へ向くベクトルが少ない場合も発散は定義できます。

2 定義
3次元の場合の定義は以下です。
$$\nabla \cdot \boldsymbol {f} = \frac {\partial {f_x}} {\partial {x}} + \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_z}} {\partial {z}} $$
\(\boldsymbol {f}\)はベクトル場、\(f_x\)は \(\boldsymbol {f}\) の\(x\)成分(スカラー)、 \(f_y\)は \(\boldsymbol {f}\) の\(y\)成分(スカラー) 、 \(f_z\)は \(\boldsymbol {f}\) の\(z\)成分(スカラー) です。
\( \nabla \cdot \)はこの後に続くベクトル場の発散を意味します。
\( \nabla \cdot \)ではなく\(\boldsymbol{div}\)を使う場合もあります。
3 発散の意味
定義をイメージで理解しましょう。
3.1 概要
図のように微小な立方体があるとします。図には描いていませんが、この立方体の内外にベクトル場\(\boldsymbol {f}\)が存在します。

\(\boldsymbol{i}\)、\(\boldsymbol{j}\)、\(\boldsymbol{k}\)をそれぞれの単位ベクトルとします。
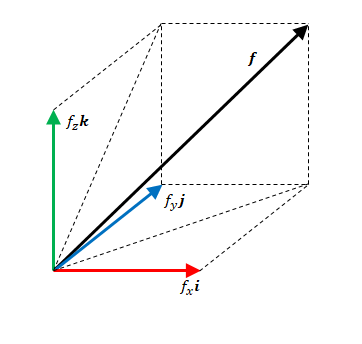
立方体の表面に垂直な\(\boldsymbol{f}\)の成分を求めます。ただし絶対的な値ではなく、向かい合う面の成分との相対値として求めます。立方体から流出する方を正、立方体へ流入する量を負として、その和を「流出量」とよぶことにします。そしてこの流出量を発散の定義と照らし合わせ関係を求めます。
3.2 2点における流出量
相対する2面の各1点に存在する\(x\)方向の成分を取り出し、流出量を求めます。

どうやれば求められるでしょう。
\(f_x\)の\(x\)方向の傾き、つまり\(x\)の増分に対する\(f_x\)の増分の割合は\( \displaystyle \frac {\partial {f_x}} {\partial {x}} \) です。
また、両者の距離は\(\Delta x\)です。

したがって、2点における流出量は \( \displaystyle \frac {\partial {f_x}} {\partial {x}} \Delta x \) です。
3.3 2面の流出量
前節では2点の流出量を求めましたが、次に2面の流出量を求めます。
立方体表面のベクトル場は一様とは限りません。本来は\(\displaystyle \frac{\partial f_x}{\partial x}\)を面全体で積分すべきところですが、微小な領域であるため一様であるとして近似で表します。
一様であれば面積を掛けるだけです。面積は\(\Delta x \Delta y\)です。したがって2面の流出量は、
$$\frac{\partial f_x}{\partial x}\Delta x \Delta y \Delta z$$
です。

3.4 残り2組の流出量
前節では2面の流出量を求めました。次に立方体の表面全体について求めます。
6面あるので前節の場合を含め同じような組み合わせが3通りあります。以下が残り2通りです。
それぞれの流出量は図に書いた通りです。

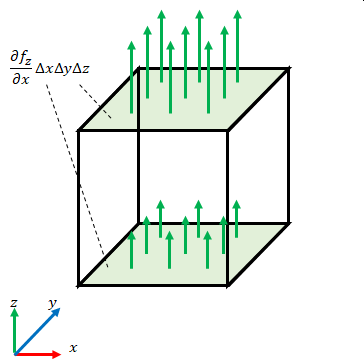
3.5 立方体全体の流出量
3通りの組み合わせを全て足し合わせると、
$$\left( \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_y}} {\partial {y}} \right) \Delta x \Delta y \Delta z $$
となります。
3.6 発散の導出
前節の式と発散の定義(下記)を比較してみましょう。
$$ \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_y}} {\partial {y}} $$
\(\Delta x \Delta y \Delta z\)の有無が違うだけですね。したがって前節の式を\(\Delta x \Delta y \Delta z\)で割れば定義と等しくなります。
つまり、発散は単位体積当たりの流出量を示しています。
4 発散の例
グラフにてベクトル場と発散の対応を見てみましょう。
ベクトル場は黒の矢印で示しています。\(x\)と\(y\)は水平方向です。ベクトル場としては2次元なので縦方向は意味はありません。前章まで、3次元のベクトル場について説明してきましたが、2次元でも同様です。本章では\(z\)に関する項が除外されたと考えてください。
発散は面で表示しています。縦方向が発散の値です。また、色でも表しており、赤が濃くなるほど大きく、青が濃いほど小さい値です。発散の面にモアレ(縞模様)が見えるかもしれませんが、作成上の都合によるもので、いずれも本来はないものです。ご了解ください。
4.1 例1
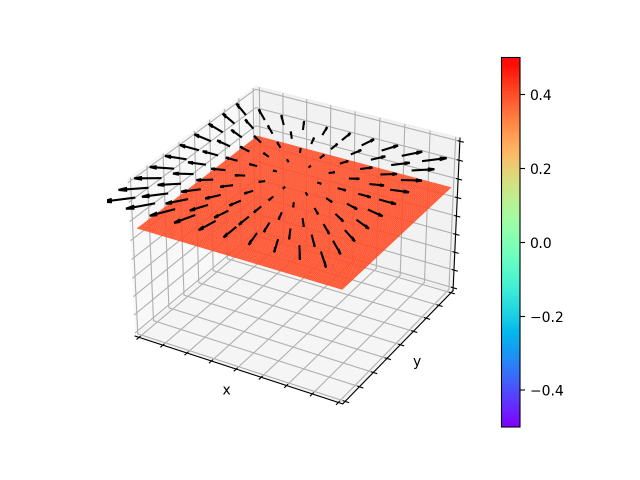
中心から放射状に広がるベクトル場です。
以下の式で表されます。
ベクトル場:
$$\boldsymbol{f}(x,y) = a (x \boldsymbol{i} + y\boldsymbol {j}) $$
発散:
$$\nabla \cdot \boldsymbol {f}(x,y) = 2a $$
いたるところで流出しており、発散は一定の値です。
4.2 例2
中心に集まるベクトル場です。
ベクトル場:
$$\boldsymbol{f}(x,y) = -a (x \boldsymbol{i} + y\boldsymbol {j}) $$
発散:
$$\nabla \cdot \boldsymbol {f} = -2a $$
前節とは逆に一定の負の値です。

4.3 例3
\(x\)方向は中心に集まり\(y\)方向は外へ向くベクトル場です。
ベクトル場:
$$\boldsymbol{f}(x,y) = a (x \boldsymbol{i} – y\boldsymbol {j}) $$
発散:
$$\nabla \cdot \boldsymbol {f} = 0 $$
発散は場所によって変化しているようにみえますが、 \(x\)方向の偏微分と\(y\)方向の偏微分の値が正負逆の同じ大きさなので相殺し常に0になります。

4.4 例4
\(x\)方向と\(y\)方向それぞれに三角関数を使用しています。
ベクトル場:
$$\boldsymbol{f}(x,y) = a (\sin (bx) \boldsymbol{i} + \sin(by) \boldsymbol {j}) $$
発散:
$$\nabla \cdot \boldsymbol {f} = ab (\cos (bx) \boldsymbol{i} + \cos(by) \boldsymbol {j}) $$
中央はベクトルが外へ広がっているため正、四隅はベクトルが集まっているために負になっています。

5 まとめと補足
・ 発散とはベクトル場の流出(湧き出し)、流入(吸い込み)をスカラー場で表現する演算です。
・発散は以下で表されます。
$$\nabla \cdot \boldsymbol {f} = \frac {\partial {f_x}} {\partial {x}} + \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_z}} {\partial {z}} $$
または
$$\boldsymbol {div} \boldsymbol {f} = \frac {\partial {f_x}} {\partial {x}} + \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_z}} {\partial {z}} $$
・微小な立方体を仮定し、立方体からの流出量求め、その直方体の体積で割ることによって上の式が導出されます。
・\(\nabla\)をベクトルと見立てると、 \(\nabla \cdot \boldsymbol{f}\)はベクトルの内積と同じ演算です。 以下のように変形すれば一致することがわかります。
$$\nabla \cdot \boldsymbol {f} = \frac {\partial {f_x}} {\partial {x}} + \frac {\partial {f_y}} {\partial {y}} + \frac {\partial {f_z}} {\partial {z}} $$
$$\nabla \cdot \boldsymbol {f} = \frac {\partial {\boldsymbol{f}}} {\partial {x}} \cdot \boldsymbol {i} + \frac {\partial { \boldsymbol{f} }} {\partial {y}} \cdot \boldsymbol {j} + \frac {\partial { \boldsymbol{f} }} {\partial {z}} \cdot \boldsymbol {k} $$
$$\nabla \cdot \boldsymbol {f} = \left ( \frac {\partial {}} {\partial {x}} \boldsymbol {i} + \frac {\partial {}} {\partial {y}} \boldsymbol {j} + \frac {\partial {}} {\partial {z}} \boldsymbol {k} \right) \cdot \boldsymbol {f} $$
