前ページではガウスの法則について説明しましたが、これは電場(電気)に関するものでした。磁場(磁気)に関してもガウスの法則があります。本ページでは磁場に関するガウスの法則について説明します。
電気と磁気の性質はよく似ています。ガウスの法則も電気と磁気では基本的に共通ですが、磁気には電気における電荷に相当するものが存在しないために方程式は異なっています。このことから磁場に関するガウスの法則は「(単)磁荷不在の法則」とも呼ばれます。本ページでは電気と磁気の相違点を中心に説明します。
微分形
$$ \nabla \cdot \boldsymbol{B} = 0 $$
積分形
$$ \oint_S \boldsymbol{B} \cdot d\boldsymbol {S} = 0$$
0 名称について
・冒頭の通り、ガウスの法則は電気・磁気どちらにも適用されます。マクスウェルの方程式4つのうち、2つがこれらガウスの法則です。本サイトでは前者を「ガウスの法則」、後者を「磁場に関するガウスの法則」とします。区別が必要な場合は前者の先頭に「電場に関する」をつけます。
・磁気に関する物理量に「磁場」と「磁束密度」があります。電気における「電場」と「電束密度」の区別と同じように別の物理量です。しかしどちらも「磁場」ということが多いため、本サイトでは 「磁場\(\boldsymbol {H}\)」、 「磁場\(\boldsymbol {B}\)」とよぶことがあります。区別が不要な場合は単に「磁場」とよびます。
1 磁場(磁場\(\boldsymbol{H}\))・磁束密度(磁場\(\boldsymbol{B}\)) 他
磁気に関する物理量について説明します。
末項に電気と磁気に関する物理量をまとめたので、後で確認ください。
1.1 磁荷(磁極の大きさ)・磁束
永久磁石や電磁石は鉄などの金属を引き付け、互いにひきつけ合ったり反発したりします。この現象の元となる物理量が磁荷(または磁極の大きさ)です。
単位はWb(ウェーバー)です。磁石におけるN極は磁荷では正、S極は負として表されます。
ただし、仮想的な意味で磁荷を扱うことはありますが、現在のところ実際に磁荷は存在しません。
同じ単位で表される物理量に磁束があります。磁気の流れを束として見立てたものです。磁束は観測可能という意味で存在します。
1.2 磁場(磁場\(\boldsymbol{H}\))・磁束密度(磁場\(\boldsymbol{B}\))・透磁率
磁荷があることによって周囲に発生する物理量に磁場と磁束密度があります。通常、前者を\(\boldsymbol {H}\)、後者を\(\boldsymbol {B}\) で表します。
磁荷と観測点の間に物質があると観測点における磁場は変化します。これは磁化(後述)いう現象によるものです。磁化によって磁場が変化する割合を透磁率で表します。一般的に\(\mu\)を使います。
真空における透磁率は一般的に\(\mu_0\)を使います。真空では磁化は発生しません。本サイトでは真空のみを対象とするので磁化は式には含まれていません。
磁場と磁束密度は以下の関係があります。
$$\boldsymbol {B} = \mu_0 \boldsymbol {H} $$
電場・電束密度・誘電率の関係(下記)と似ています。
$$\boldsymbol {D} = \epsilon_0 \boldsymbol {E} $$
磁束密度のことを単に磁場とよぶことが多いので、本サイトでは磁場\(\boldsymbol {H}\)と磁場\(\boldsymbol{B}\)として区別します。以降磁束密度は使いません。
1.3 磁力線・磁束線
電気力線・電束線と同じように磁場も連続した線で表すことができます。磁場\(\boldsymbol{H}\)を表す線を磁力線、磁場\(\boldsymbol{B}\)を表す線を磁束線とよびます。
1.4 磁気モーメント
磁気モーメントは磁石の強さと向きを表すベクトルです。
磁気モーメントは後述の磁気双極子や永久磁石の説明で使います。
磁荷と何が違うのでしょう。
磁荷\(q_m\)と\(-q_m\)が位置\(\boldsymbol{d}\)だけ離れていたとします。
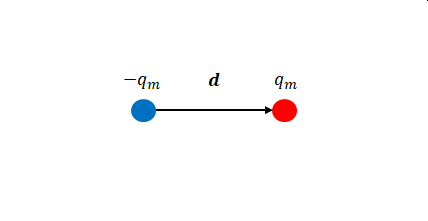
両者により発生する磁気モーメントは
$$\boldsymbol{m} = q_m \boldsymbol {d}$$
と表されます。
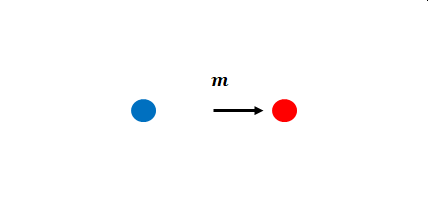
ただし(少なくとも現在は)実際には単極の磁荷は存在しません。
また、円を描く電流\(I\)においても磁気モーメントは発生します。この場合、電流の経路が囲む領域の面積\(\boldsymbol{S}\)に対し、
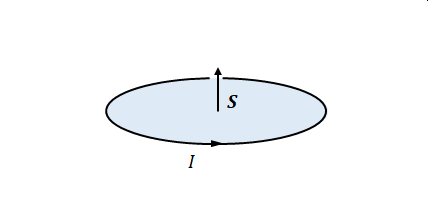
$$\boldsymbol{m}= I \boldsymbol{S}$$
と表されます。
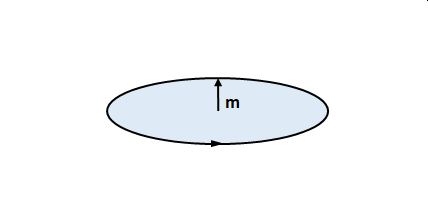
\(\boldsymbol{S}\)と\(\boldsymbol{m}\)のベクトルの向きは電流を時計回りになるよう見た場合に手前から奥です。
2 磁気双極子
電場に関するガウスの法則と磁場に関するガウスの法則は似ているのですが、右辺が異なります。磁気双極子は存在するが磁気単極子が存在しないことが相違の原因です。
本章で電気双極子・磁気単極子・磁気双極子について説明します。なお、電気単極子は存在しますが、あまりこの名ではよばれず単に点電荷とよばれます。
2.1 電気双極子
電場に関するガウスの法則のページで誘電分極について簡単に説明しました。外部より電場を加えることにより原子・分子内の正と負の電荷が偏っている状態です。この正と負の電荷が対になっている状態が電気双極子です。誘電体内部で分極が起きているとき、この電荷の対は電気双極子です。ただし電気双極子は分極以外の条件でも存在します。
電気力線で表すと下の図のようになります。赤・青が電荷です。
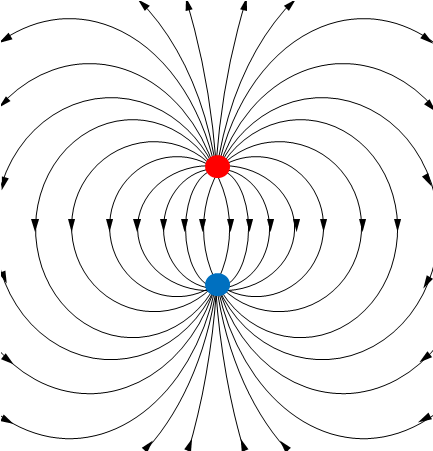
2.2 磁気単極子
棒磁石にはN極とS極があります。
これを半分に切るとどうなるでしょう。
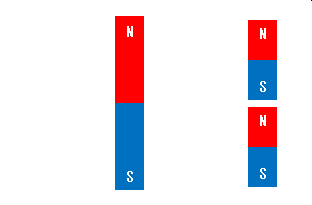
切った後の両方にそれぞれN極とS極が現れます。これらをさらに切っても同じようにいずれの断片にもN極とS極があります。
点電荷は正または負いずれかが単独で存在することができます。しかし、磁石を切断してもそれぞれにN極とS極が存在することからわかるように、N極(正の磁荷)またはS極(負の磁荷)が単独で存在することができません。磁気に関しこれに相当するものがありません。
ただし、現時点で存在が確認できていないという意味であり、理論上は存在が否定されているわけではありません。この、正と負の磁荷が対になった仮想の粒子を磁気単極子とよびます。
マクスウェルの方程式は磁気単極子が存在しないものとして記述されています。
2.3 磁気双極子
磁気単極子は現在存在を確認できていませんが、磁気双極子は存在します。その構造には2通りの考え方があります。
一つは、電気双極子と同じように磁荷\(+q_m\)と\(-q_m\)が対になっているという考え方です。。

ただし、実際には磁荷\(+q_m\)と\(-q_m\) の粒子が単独で存在するわけではありません。正と負の磁荷が対になって存在するわけではありません。正と負の磁荷の対を磁気双極子とよぶ場合は仮想の概念です。
もう一つは円周上を流れる電流という考え方です。これは実在します。アンペールの法則の通り、円の面を垂直に横切るよう磁場が発生します。下の赤の矢印が電流です。
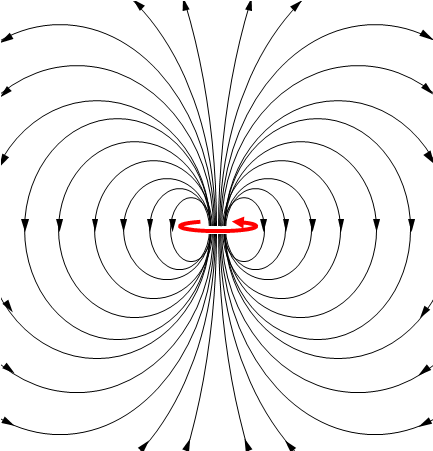
では磁場を発生する物質の内部では電流が流れているのでしょうか。
電流とは電荷の移動によって生じるものです。例えば乾電池に豆電球と銅線を接続した場合、銅線内で大量の電子が移動します。これは負の電荷が移動している状態です(逆方向に正の電荷が移動していると考えることもできます)。
しかし電流は金属の線の中を流れるとは限らないし、大量の電荷が移動する必要はありません。真空中でごく少量の点電荷が動いていたとしても電流です。
さて、磁荷の対と電流、どちらが正しいのでしょう。前述の通り実際に前者のような構造が存在するわけではありません。実在する磁気モーメントは全て後者によるものです。現実に即しているのは後者です。ただし仮想の概念として前者を指す場合もあります。
後者の場合、磁気双極子は無限小の電流であるとされる場合もあれば、単に微小な電流と表現される場合もあります。いずれにしても正と負の磁荷は不可分で、磁気モーメントをもつ物質は磁気双極子の集合体であると考えてください。
3 電場と磁場に関するガウスの法則の相違
電場と磁場の性質は対称になるはずですが、ガウスの法則ではやや異なります。電場に関する法則の右辺では電荷と誘電率の項があったのに対し、磁場に関する項の右辺は0になるという違いがあります。なぜこの違いがなぜ生じるのでしょう。
以下、磁束線・電気力線を見比べて考えてみましょう。
3.1 なぜ積分形の式の右辺が0になる?
まず電場に関してです。
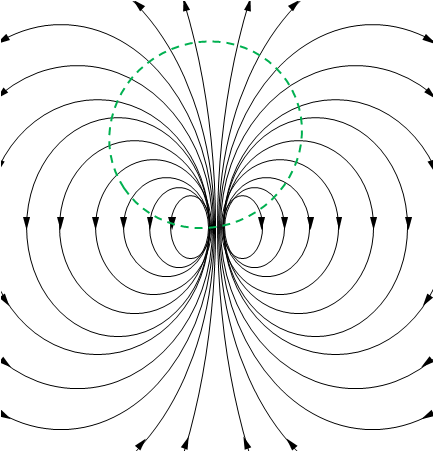
下図の赤丸は電荷、緑の点線の内側は対象の領域です。
領域の中に電荷があった場合、式の右辺は0以外の値になります。
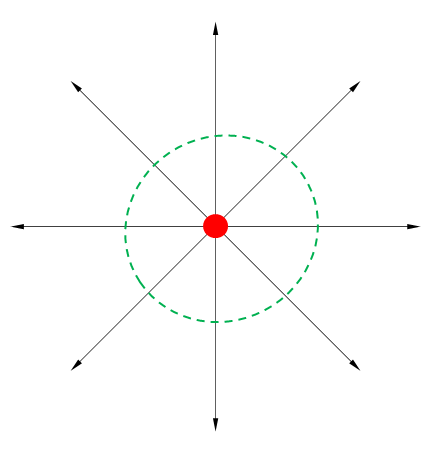
磁束線が境界と交差するところは必ず外を向きます。
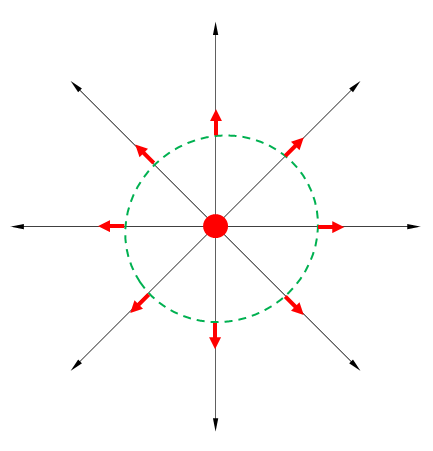
領域の外のみに電荷があった場合、式の右辺は0です。
図の領域は流入と流出が同量なので0になります。
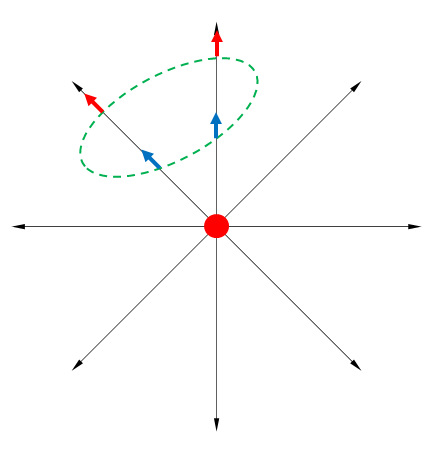
次に磁場\(\boldsymbol{B}\)に関してです。
磁気双極子を含まない領域について考えてみます。
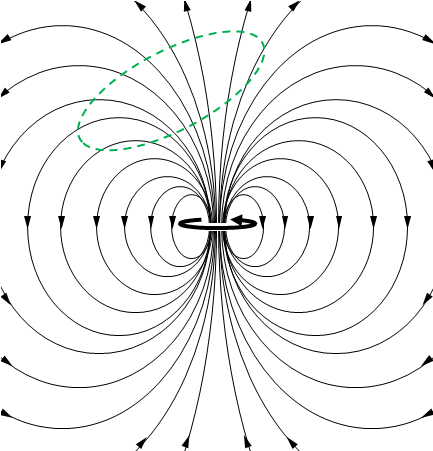
電荷を含まない領域に入る電気力線と領域から出る電気力線の数が同じになりましたが、磁気双極子でも同じように領域に入る磁束線と出る磁束線の数は同じになります。
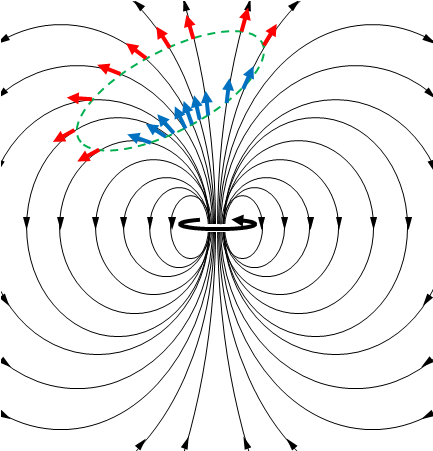
領域の外に磁気双極子があった場合も領域から出る磁束と領域に入る磁束の量は同じです(赤と青の矢印は省略します)。
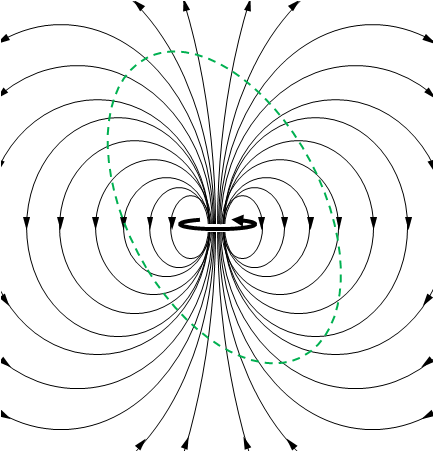
3.2 永久磁石の中間に境界があった場合はどうなる?
下の図のように境界が磁石のN極とS極の間を通ったらどうでしょう。磁束線はN極より出るので流出のほうが多くなるのではないでしょうか。
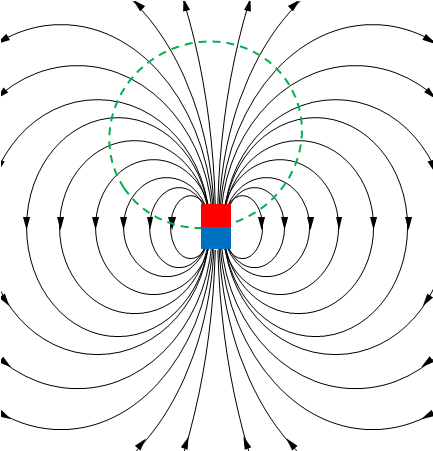
磁石では磁束線の流れがわかりにくいので、磁気双極子の集合体であると考え、その1個に注目してみましょう。1個について結論が出れば、重ね合わせの原理にて磁石について考えることができます。
さて、電気単極子の周囲では電気力線が放射状に伸び、その線は戻ってきません。磁気双極子の周辺の磁束線が違うのは、必ず線が閉じているところです。中央付近から出た線は大きな軌跡を描きますが、いずれも元の位置に戻り繋がります。分岐も合流もありません。
したがって、どこの場所で閉領域をとっても、必ず出る本数と入る本数は同じになります。
3.3 なぜ微分形の式の右辺は0になる?
積分形の右辺が0になるのであれば、微分形の右辺も0になるのは容易に理解できます。
しかし磁気双極子周辺の磁束線を見ると、密度が変化しています。磁束の発生源から外へ向かう線は広がっており、発生源へ向かう線は収束しています。本当にどこでも発散は0になるのでしょうか。
以下はベクトル場の発散のページに掲載した図です。比較のためにここでも掲載しました。黒の矢印は2次元のベクトル場を表しています。発散を高さ方向と色によって表しています。この場合はオレンジ色の部分です。いたるところで正の値を示しています。つまり流出があります。
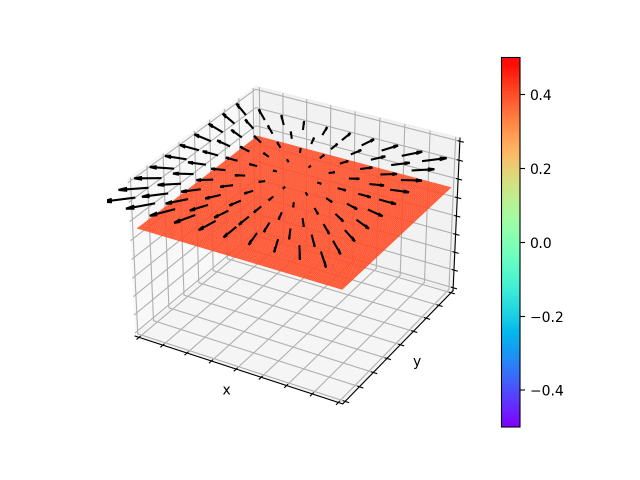
上図と磁束線の図は何が違うのでしょう。
磁束線は途中で分岐や合流することはありません。このことが流出量が0であることを示しています。
磁束線が広がっているところは発散しているようにみえますが、線の間隔が疎になるので磁場が弱まっていることでもあります。線が密になるところはその逆です。
一方、上の図の黒の矢印は中心から外へ向かうほど大きくなっています。つまり、いたるところ流出があることを示しています。つまりこのような状態は磁束線では表せません。
磁束線は分岐も合流もなく必ず閉じています(始点も終点もありません)。これは発散が0であるということを示しています。
3.4 右辺が0ということは磁場は存在しない?
磁場に関するガウスの法則の式からわかるように、領域からの 磁場\(\boldsymbol{B}\) の流出量の総和は0です。では、例えば永久磁石の周囲には磁場がないのでしょうか。流出量の総和は0ですが、個々の点における磁場\(\boldsymbol{B}\)は0とは限りません。磁場に関するガウスの法則は流出量が0であるということを示しているだけであって、特定の点における磁場\(\boldsymbol{B}\)を示しているわけではないからです。
参考まで、円電流により発生した磁気双極子が原点にある場合、位置\(\boldsymbol{r}\)における磁場\(\boldsymbol{B}(\boldsymbol{r})\)は以下のように表されます。\(boldsymbol{m}\)は磁気モーメントです。
$$\boldsymbol{B} ( \boldsymbol {r} ) = \frac {1} {4 \pi}\left( \frac{3(\boldsymbol{m} \cdot \boldsymbol{r}) \boldsymbol{r}} {r^5} – \frac{\boldsymbol{m}}{r^3}\right)$$
磁荷の対による磁気双極子の場合も、十分に遠い場所においては近似により同じ式になります。ただし近傍では大きさも向きも異なります(詳細は省略します)。
4 E-B対応とE-H対応の違い
4.1 なぜE-B対応では磁場\(\boldsymbol{H}\)ではなく磁場\(\boldsymbol{B}\)で表す?
電場に関するガウスの法則は電荷と電場を使って表されます。電場と対称にするのであれば磁場に関するガウスの法則は磁場\(\boldsymbol{H}\)を使うべきです。
しかし本サイトでは磁場ではなく磁場\(\boldsymbol {B}\)を使って表しています。
これはマクスウェルの方程式をE-B対応で表しているからです。
E-H対応であれば、以下のように磁場\(\boldsymbol{B}\)ではなく磁場\(\boldsymbol{H}\)を使います。
微分形
$$ \nabla \cdot \boldsymbol{H} = 0 $$
積分形
$$ \oint_S \boldsymbol{H} \cdot d\boldsymbol {S} = 0$$
電気に関する法則で電場を使うのであれば磁気に関しては磁場\(\boldsymbol{H}\)が対応するはずです。
ではなぜE-B対応では磁場\(\boldsymbol{B}\)を使うのでしょう。
比較のために、まずE-H対応について考えてみましょう。
E-H対応は磁荷の周囲に磁場が発生するという考え方です。実際には磁荷は存在しませんが、正負の対になった磁荷によって構成された磁気双極子モーメントによって磁場が発生するという考え方です。
磁荷と磁場の関係は以下のクーロンの法則より導くことができます。
$$\boldsymbol{F}=\frac{1}{4\pi \epsilon_0} \frac {q_{m1}} {q_{m2}}$$
\(\boldsymbol{F}\)は力、\(q_{m1}\)、\(q_{m2}\)は磁荷です。
詳細は省略しますが、ここから磁荷と磁場\(\boldsymbol{H}\)の関係が得られるという考え方です。
正しくは磁荷ではなく円電流によって磁気双極子が発生します。
したがって、電流によって磁場が発生するという考え方で表された式がE-B対応です。
電流と磁場の関係はビオ=サバールの法則によって表されます(下記)。
$$d\boldsymbol{B} = \frac{\mu_0}{4\pi} \frac{I d \boldsymbol{l} \times \hat{\boldsymbol{r}} } {r^2}$$
\(I\)は電流、\(\boldsymbol{l}\)は仮想的に電流の経路を切り取ったベクトル(流れる方を向く)、\(r\)は電流から観測点までの距離\(\hat{\boldsymbol{r}}\)は電流から観測点を向く単位ベクトルです。
\(d\boldsymbol{l}\)は電流の経路を微小な距離で切り取ったもの(電流素片)です。
また、ビオ=サバールの法則ではなくローレンツ力(下記)がE-B対応の場合の出発点とする場合もあります。
$$\boldsymbol{F}=q\boldsymbol{v}\times \boldsymbol{B}$$
\(\boldsymbol{F}\)は力、\(q\)は電荷(磁荷ではありません)、\(\boldsymbol{v}\)は電荷の速度、\(\times\)は外積です。
または以下のように表される場合もあります。
$$\boldsymbol{F}=I d \boldsymbol{l} \times \boldsymbol{B}$$
ローレンツ力よりビオ=サバールの法則を導くことができるので、いずれも電流と磁場\(\boldsymbol{B}\)の関係が示されていることになります。
以上のように、E-H対応は磁荷を基準とするために磁場\(\boldsymbol{H}\)、後者は電流を基準とするために磁場\(\boldsymbol{B}\)が使われます。
5 磁化
本サイトでは磁場に関するガウスの法則を真空状態のみに限定しています。真空では磁化は発生しないため直接は関係ありませんが参考として簡単に説明します。
5.1 スピン磁気モーメント
円電流によって磁気双極子が定義されるとすれば、永久磁石が金属を引き付けたり磁石同士で反発したりするのはなぜでしょう。
永久磁石の磁気モーメントも電流によるものだからです。
実は理由を正確に知るには量子力学の知識が必要なのですが、ここでは概要だけ説明します。
永久磁石を切断するとそれぞれの断片がN極とS極をもつという話をしました。では切断を続け、やがて原子・分子1個になるとどうでしょう。
この1個も磁力、つまり磁気モーメントがあります。
では永久磁石を構成していた原子・分子の磁気モーメントの発生源は何でしょう。
原子を構成する電子はスピンをしています。スピンによって磁気モーメントが発生します。これをスピン磁気モーメントとよびます。
原子核を太陽、電子を地球に例えるなら、地球の自転がスピンです。ただし、これは正確な表現ではありません。正確なスピンのふるまいを知るには量子力学が必要です。スピンによって磁気モーメントが発生する理由を知るにも量子力学が必要です。とりあえずは電子のスピンによって磁気モーメントが発生するものとだけ理解ください。
原子の中の電子の多くは対になっています(対電子)。対電子の磁気モーメントの方向は互いに逆になっています。磁気モーメントは相殺されます。
しかし、原子・分子の種類や状態によっては対ではない、単独の電子が存在します(不対電子)。したがって不対電子が存在する場合はこの電子の磁気モーメントが原子・分子の磁気モーメントとなります。複数の不対電子が存在する場合、これらの向きは同じなので、不対電子の数だけ磁気モーメントが発生します。
5.2 なぜ永久磁石は磁気モーメントをもつ?
原子・分子が磁気モーメントをもつ理由は前節の通りですが、物質が磁力をもつ理由にはもう少し続きがあります。
永久磁石が磁気モーメントをもつのは強磁性という性質によるものです。他に、物質によっては常磁性・反磁性という性質をもつものもあります。これらについても簡単に説明します。
強磁性:
外部から磁場を印可すると強い磁気モーメントをもちます。磁気モーメントの方向は印可された磁場と同じです。外部の磁場がなくなった後も磁気モーメントが残ります。これを自発磁化とよびます。外部磁場がなくても永久磁石が磁気モーメントをもつのは自発磁化によります。
外部から磁場を印可されず自発磁化もする前の物質に磁気モーメントがないのはなぜでしょう。
強磁性の物質は前述のようにスピン磁気モーメントをもちます。しかし磁場がなく自発磁化前であれば個々の原子・分子のスピン磁気モーメントの向きはバラバラです。したがって物質全体としては相殺され磁気モーメントをもちません。
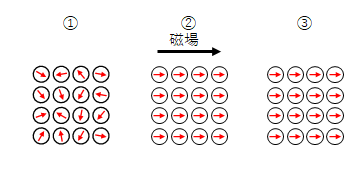
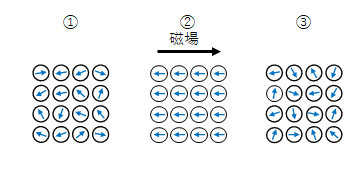
外部から磁場が与えられるとスピン磁気モーメントの向きがそろいます。個々のスピン磁気モーメントの和が現れます。そして磁場がなくまってもスピン磁気モーメントの向きが保たれるため自発磁化となります。
下の図①-③は時間順と考えてください。
常磁性:
外部から磁場を印可されているときのみ磁気モーメントをもちます。磁気モーメントの方向は印可された磁場と同じです。
強磁性と異なるのは、磁場を印可されているときの磁気モーメントは比較的弱く、磁場を印可されないときは常に磁気モーメントをもたない点です。
常磁性も強磁性と同じく、磁場を印可されているときスピン磁気モーメントの向きがそろいます。磁場を印可されていないときは常にスピン磁気モーメントの向きがバラバラになります。
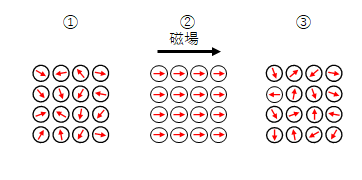
反磁性:
外部から磁場を印可されているときのみ磁気モーメントをもちます。磁気モーメントの方向は印可された磁場とは反対です。
反磁性は強磁性・常磁性とは異なりスピン磁気モーメントによるものではありません。原子が原子核の周りを公転することによって生じるモーメントが関係します。これを軌道磁気モーメントとよびます。
外部から磁場が印可されると、その磁場を弱めるような電流が流れるという法則があり、これをレンツの法則とよびます。つまり外部から磁場が加えられるとこれとは逆方向の軌道磁気モーメントが発生するよう各原子・分子の軌道が変わります。これが反磁性の発生源です。
強磁性と常磁性は特定の物質のみが示す性質です。強磁性と常磁性の両方をもつこともありません。
反磁性は全ての物質に存在します。しかし非常に弱いために強磁性や常磁性をもつ物質は反磁性の性質が相殺され現象となって現れません。
水などは反磁性のみを示します。拙著で水の反磁性によって起きる現象について簡単に述べています。よろしければご覧ください。
結局、永久磁石の磁気モーメントの発生源は何でしょう。直接は電子のスピン磁気モーメントです。電子のスピン磁気モーメントの詳細はここでは説明していませんが、磁気モーメントの向きを軸とする円電流がその発生源であると考えられます。したがって、永久磁石の磁気モーメントは物質内部の円電流によるものです。
5.3 磁化
磁化とは、物質に外部より磁場を与えることにより物質が磁石の性質をもつことです。磁場がなくなった後も磁石の性質を維持する場合もありますが、これも含むことがあります。また、単位体積当たりの磁気モーメントを磁化のベクトルとして表します。
前節の通り、原子・分子にはスピン磁気モーメントと軌道磁気モーメントがあります。ただし、磁化されていない状態では方向がばらばらであるため物質としては磁気モーメントがありません。
磁化されることによって向きがそろい、磁気モーメントをもちます。
6 まとめ
・磁場に関するガウスの法則は電場に関するガウスの法則と似ていますが、右辺は0になります。
・電場の法則と異なるのは、磁気単極子が存在しないからです。そのために必ず領域の境界からの流出量が0になります。
・E-H対応では磁場\(\boldsymbol{H}\)、E-B対応では磁場\(\boldsymbol{B}\)を使います。
E-H対応では磁荷の対によって磁気双極子が構成され、磁荷により磁場\(\boldsymbol{B}\)が発生するという考え方を基にしています。
E-B対応では、電流により磁気双極子が発生し、磁場\(\boldsymbol{B}\)が発生するという考え方を基にしています。の違いです。
磁荷によって磁気双極子は作られないので現実に忠実なのは後者といえます。
・真空でない場合には磁化により磁場\(\boldsymbol{H}\)と\(\boldsymbol{B}\)の関係は変化します。この係数を誘電率\(\mu\)で表します。本サイトでは真空の場合(誘電率は\(\mu_0\))のみを対象とします。
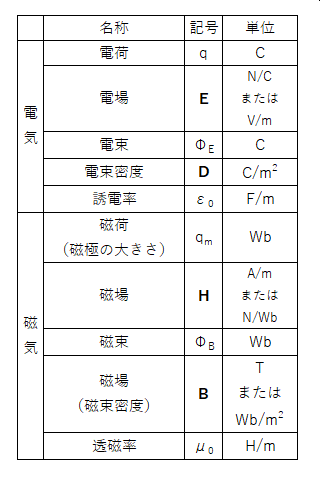
・下の表は電気と磁気に関する物理量です。