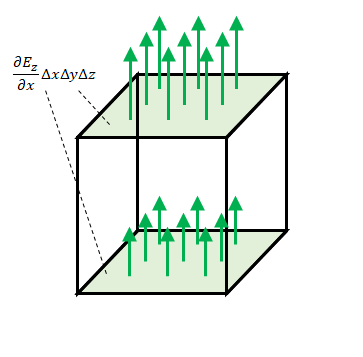
4つの方程式のうちの1つであるガウスの法則について説明します。
微分形
$$\nabla \cdot \boldsymbol{E} = \frac {\rho} {\epsilon_0} $$
積分形
$$ \oint_s \boldsymbol{E} \cdot d\boldsymbol {S} = \frac{1}{\epsilon_0} \int_V \rho dV$$
1 電荷・電場・誘電率・電気力線の定義
1.1 電荷
紙と下敷きをこすると引き寄せられますね。その状態の下敷きが帯びているものが電荷です。
電荷には正と負があります。陽子は正、電子は負です。
単位は\(C\)（クーロン）です。
スカラーで表します。
小さな点が帯電している場合、これを点電荷とよびます。
1.2 電場
電場は電荷の周囲に生じるベクトル場です。
電場はクーロン力より定義されます。
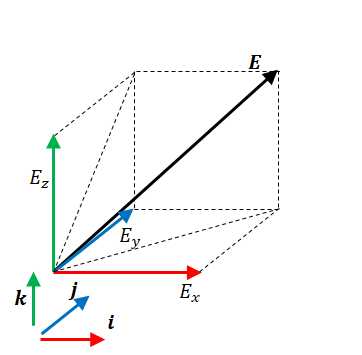
力を\(\boldsymbol{F}\)、電荷を\(q\)、電場を\(\boldsymbol{E}\)、磁場を\(\boldsymbol{B}\)、電荷の移動速度を\(\boldsymbol {v}\)とすると以下の関係にあります。
$$\boldsymbol{F}=q\boldsymbol{E} $$
以下のように\(\boldsymbol{E}\)の中に\(q\)が存在すると、
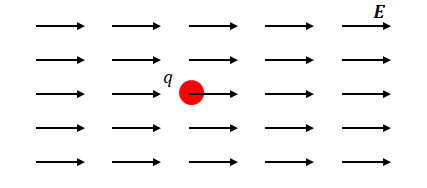
力\(\boldsymbol{F}\)がはたらきます。
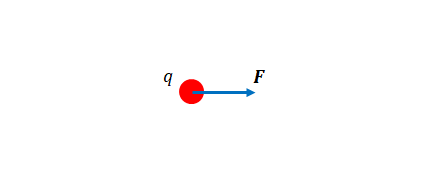
電場の単位は\(N/C\)です。\(N\)（ニュートン）は力の単位です。
つまり、\(|\boldsymbol{E}|=1[N/C]\)の電場に\(q=1[C]\)の電荷がある場合、
電荷に\(|\boldsymbol{F}|=1[N]\)の力がはたらきます。
また、電場 は\(V/m\) でも表すことができます。\(V\)は電圧（電位）、\(m\)は距離の単位です。電圧との関係はファラデーの法則のページで説明します。
クーロン力に磁場\(\boldsymbol{B}\)、電荷の移動速度\(\boldsymbol {v}\)を加えると以下の関係になります。
$$\boldsymbol{F}=q(\boldsymbol{E} + \boldsymbol{v} \times \boldsymbol{B})$$
これをローレンツ力とよびます。
1.3 誘電率
電荷の周囲には電場ができます。電場を観測する点と電荷の間に物質（固体・液体・気体）が存在すると誘電分極（以下分極）が起きます。分極は6章で簡単に説明します。
誘電率は分極の起きやすさと関係があります。分極の起きやすさそのものを示しているわけではありませんが、誘電率が大きいほど分極が起きやすくなります。
分極によって電場は弱くなります。誘電率は電場の弱まり方を示しています。
誘電率は物質によって固有の値をもちます。
一般的に\(\epsilon\)で表されます。特に真空の場合を\(\epsilon_0\)とします。本サイトのガウスの法則は\(\epsilon_0\)を使って表しています。
単位は\(F/m\)です。\(F\)（ファラッド）はコンデンサの容量を示します。\(1[F]\)のコンデンサに\(1[C]\)の電荷がたまっているとき両極に\(1[V]\)（ボルト）が発生します。
1.4 電気力線
電場を向きに沿って1本の線でつないだものを電気力線とよびます。実在するものではなく、仮想の線です。線のあるところだけに電場が存在するわけでもありません。連続的な場を離散的に表現しているだけです。
線の本数には意味があり、電場が強いところでは密、弱いところでは疎になります。
途中で分岐・合流・交差することはありません。
電気力線の総量は単位を本として表します。\(1[C]\)の電荷に対し、\(\frac{1}{\epsilon}[本]\)の電気力線があります。
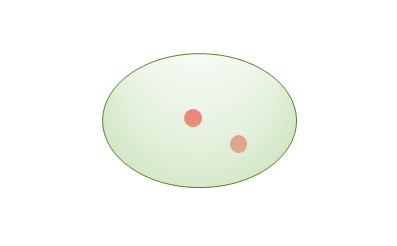
以下は電気力線の例です。赤の丸は正、青の丸は負の点電荷です。
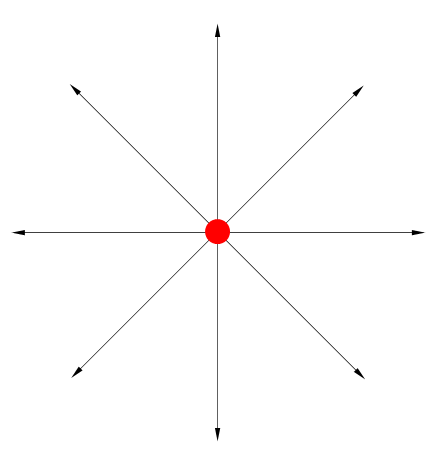
電気力線は静電場の分布や流れを表すためによく使われます。電気力線は分岐も合流もしないという点が優れているからなのでしょう。
なぜ分岐・合流なしに線を描くことができるかというと、（電荷があるところ以外では）電場の湧き出し（流出）も吸い込み（流入）もないからです。
この段階では何のことかわからないと思いますが、ガウスの法則を知れば理解できると思います。
2 微分形
2.1 物理量と記号の意味
左辺に\(\nabla \cdot\)があります。これは電場の発散を表しています。ある点において正の電荷が存在すればその点の発散が正、負の電荷が存在すればその点の発散が負になることを示しています。
微分形の右辺の\(\rho\)は電荷密度です。単位体積あたりの電荷のことです。電荷ではなく電荷密度でなければなりません。
\(\epsilon_0\)は真空における誘電率です。
2.2 発散の意味
発散については「ベクトル場の発散」にもう少しくわしく書いていますのでもしよければこちらもご覧ください。以下に、定義についてほぼ同じ内容掲載しています。「＋」を押して表示させてください。
※発散は点におけるベクトルの湧き出しの量を正、吸い込みの量を負とした場合の総和です。本ページではこれを「流出量」とよぶことにします。
発散の定義は以下です。
$$\nabla \cdot \boldsymbol {E} = \frac {\partial {E_x}} {\partial {x}} + \frac {\partial {E_y}} {\partial {y}} + \frac {\partial {E_z}} {\partial {z}} $$ \(E_x\)は \(\boldsymbol {E}\) の\(x\)成分、 \(E_y\)は \(\boldsymbol {E}\) の\(y\)成分 、 \(E_z\)は \(\boldsymbol {E}\) の\(z\)成分です。 いずれもスカラーです。
(2)直方体
下の図のような直方体があるとします。
この直方体は微小であるため表面に接する電場は一様であると近似します。
直方体からの流出はとりあえず考えません。後で追加します。
このうち、\(x\)方向に垂直な2面に接する各1本に注目します。これらを\(\boldsymbol {E} \)とします。
(3)\(x\)方向の電場
\(\boldsymbol{E}\)の\(x\)方向の成分を求めます。
\(x\)、\(y\)、\(z\)方向の単位ベクトルを \(\boldsymbol {i}\)、\(\boldsymbol {j}\)、\(\boldsymbol {k}\)とします。
また、\(\boldsymbol {E}\)の \(x\)、\(y\)、\(z\)方向の成分を \(E_x\)、\(E_y\)、\(E_z\)とします。
内積を使って $$E_x = \boldsymbol{E} \cdot \boldsymbol{i}$$ $$E_y = \boldsymbol{E} \cdot \boldsymbol{j}$$ $$E_z = \boldsymbol{E} \cdot \boldsymbol{k}$$ と表すことができます。
下図のように2面に\(E_x\)が接します。
(4)直方体からの流出の追加
上記の通り直方体からの流出はないものとしましたが、ここで直方体からの流出量を追加します。流入の場合は負です。左右に\(\frac {\Delta E_x} {2}\)の流出があるとします。
直方体に接する流出量は\( E_x + \frac {\Delta E_x} {2} \)と\( E_x – \frac {\Delta E_x} {2} \)に変わります。
(5)右の面と左の面の1点からの流出量
右の面に接するスカラーと左の面に接するスカラーの和（流出量）はどれだけでしょう。
$$ ( E_x + \frac {\Delta E_x} {2} ) – ( E_x – \frac {\Delta E_x} {2} ) = \Delta E_x$$ ですね。
偏微分を使ってこの値を表すとどうなるでしょう。
\(E_x\)の\(x\)方向の傾きは\(\frac {\partial {E_x}} {\partial {x}}\)と表すことができます。右の面と左の面の距離は\(\Delta x\)です。
流出量は傾きと距離の掛け算で表すことができます。したがって\( \frac {\partial {E}} {\partial {x}} \Delta x \)です。
両者が等しいことから以下の関係が成り立ちます。
$$ \Delta E_x = \frac {\partial {E_x}} {\partial {x}} \Delta x $$
(6)右の面と左の面全体からの流出量
微小領域であるため直方体の面に接するベクトルは一様であるとしました。\(x\)に垂直な面の面積は\(\Delta y \Delta z\)なので、2面からの流出量は
$$\Delta y \Delta z = \frac {\partial {E_x}} {\partial {x}} \Delta x \Delta y \Delta z $$ と表すことができます。
(7)直方体表面全体からの流出量
\(y\)方向、\(z\)方向も同じように求めることができます。
$$ \Delta E_y \Delta z \Delta x = \frac {\partial {E_y}} {\partial {y}} \Delta x \Delta y \Delta z $$ $$ \Delta E_z \Delta x \Delta y = \frac {\partial {E_z}} {\partial {z}} \Delta x \Delta y \Delta z $$ したがって6面全てからの流出量は
$$( \frac {\partial {E_y}} {\partial {y}} + \frac {\partial {E_y}} {\partial {y}} + \frac {\partial {E_y}} {\partial {y}} ) \Delta x \Delta y \Delta z $$ となります。
(8)発散の意味
6面からの流出量と発散を比較します。
流出量は、
$$( \frac {\partial {E_y}} {\partial {y}} + \frac {\partial {E_y}} {\partial {y}} + \frac {\partial {E_y}} {\partial {y}} ) \Delta x \Delta y \Delta z $$ 発散は、
$$( \frac {\partial {E_y}} {\partial {y}} + \frac {\partial {E_y}} {\partial {y}} + \frac {\partial {E_y}} {\partial {y}} ) $$ です。
流出量を\( \Delta x \Delta y \Delta z \)で割ると発散になります。\(\Delta x \Delta y \Delta z \)は直方体の体積です。
つまり微小直方体の流出量を単位立方体あたりに換算すると発散になります。
2.3 物理的意味
ガウスの法則の両辺を比較します。
左辺は単位体積当たりの電場の流出量でした。
右辺の\(\rho\)は電荷密度なので、単位体積当たりの電荷です。
式にすると以下の関係です。
分母を消去すると、
つまりガウスの法則の微分形は「微小領域における流出量は領域内の電荷と等しい」ということを示しています。
ここまでは微小な直方体に限定して考察しています。後述の発散定理を適用すれば任意の大きさ、形状についても該当することがわかります。
3 積分形
3.1 ベクトル場の面積分
積分形の左辺には面積分が使われていますが、高校で学習した積分とは少し違います。ここで簡単に説明します。
スカラー場・ベクトル場の面積分に、より詳細な説明があるので、よければご覧ください。
次のような閉曲面（球の面のように、開いている部分がない曲面）\(S\)と電場\(\boldsymbol{E}\)があるとします。
曲面\(S\)上の微小領域を\(\Delta S\)とします。
\(\Delta S\)の法線ベクトルを\(\Delta \boldsymbol{S}\)とします。微小領域を平面とみなし、その平面に対し垂直であるベクトルが法線ベクトルです。 垂直な方向というだけでは2通りありますが、そのどちらになるかは都度定義する必要があります。ガウスの法則の場合、閉曲面からみて外です。
\(\Delta \boldsymbol{S}\) の大きさは\(\Delta S\)の面積です。
\(\Delta S\)上に存在するベクトル\(\boldsymbol {E}\)との内積を求めます。つまり\(\boldsymbol{E} \cdot \Delta \boldsymbol {S}\)です。
これを\(\Delta S\)の位置を変えながら曲面\(S\)上全てにおいて求めた和が積分です。
和は
$$\sum_{i=1}^{n}\boldsymbol{E}_i \cdot \Delta \boldsymbol{S}_i$$
と表せます。\(n\)を大きくし\(\Delta \boldsymbol{S}\)を小さくすると
$$\lim_{n \to \infty} \sum_{i=1}^{n}\boldsymbol{E}_i \cdot \Delta \boldsymbol{S}_i = \int_{S} \boldsymbol{E} \cdot d \boldsymbol{S}$$
となります。
3.2 スカラー場の体積積分
ガウスの法則の右辺は体積積分です。
立体の体積を\(V\)、微小領域（直方体）を\(\Delta V\)、領域内のスカラーを\(q\)とすると、
$$\lim_{n \to \infty }\sum_{i=1}^{n} q \Delta V_i = \int_V q dV $$
と表すことができます。
高校では直交座標における体積の積分を習ったかもしれませんが、その\(dx dy dz\)を\(dV\)にしたものと考えてください。
3.3 物理的意味
領域\(V\)の中に点電荷\(q\)があるとします。\(V\)の表面\(S\)上の電場\(\boldsymbol{E}\)の面積分は\(q\)と同じ値になります。
点電荷が複数存在したとしても重ね合わせの原理により電場の面積分と電荷の総和は一致します。
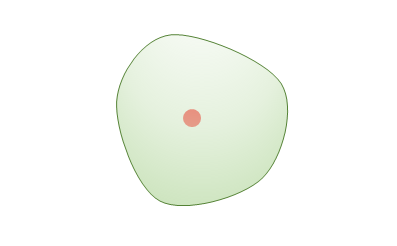
霧のように電荷が連続的に分布していたとしても電場の面積分と電荷の体積積分は一致します。
領域内の電荷が変わらなければ領域の形状や大きさが変わっても結果は同一です。
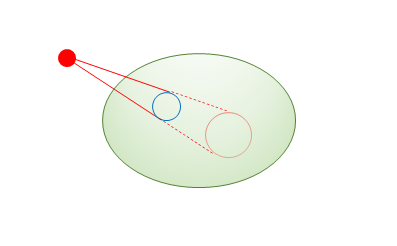
領域の外にある電荷はこの式には反映されません。図のように、領域の内側の向きの電場と外側向きの電場が相殺するからです。
4 微分形と積分形が等しいことの直観的な確認
2章と3章でガウスの法則の微分形と積分形の示す意味を考えました。
式から得られる直接の意味は異なりますが、両者の本質は同じです。
ここでは微小な領域を連結し任意の領域を形成した場合にどのように関係が変わるかを求め、両者が等しいことを導きます。
4.1 微分形と積分形の比較
改めてガウスの法則です。
微分形
$$\nabla \cdot \boldsymbol{E} = \frac {\rho} {\epsilon_0} $$
積分形
$$ \oint_S \boldsymbol{E} \cdot d\boldsymbol {S} = \frac{1}{\epsilon_0} \int_V \rho dV$$
両者の右辺を比べると、微分形を領域\(V\)で体積積分すると積分形になることがわかります。
したがって、左辺の微分形も領域\(V\)で体積積分すると積分形になるはずです。
そうであれば、以下が成立します。
$$\oint_{S} \boldsymbol{E} \cdot d\boldsymbol{S} = \int_{V} \nabla \boldsymbol {E} \cdot dV $$
これは発散定理（ガウスの定理）そのものです。次節で発散定理について説明します。
4.2 発散定理
発散定理はベクトル場の発散の体積積分と、ベクトル場の境界面について面積分が等しいとする定理です。ベクトル場に電場を適用すると前節の式が成立します。
なぜこの関係が成り立つかを考えてみましょう。
2章では微小な直方体の流出量 を単位体積に換算すると発散になることを示しました。この直方体を隙間なく並べていくことを考えます。
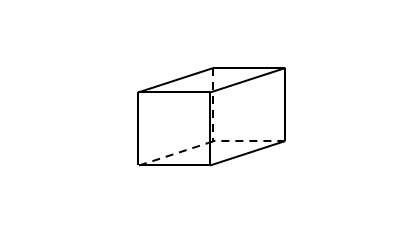
直方体を2個並べたとします。両者が接する面の流出量の和はどれだけでしょう。
下の図は直方体を分けたところです。赤は電場（ベクトル）です。分けて電場を描いていますが、同じものです。片方の直方体にとって流出が正であれば、もう片方は負です。和は0になります。
これが多数の直方体を並べると流出量の和は何を意味しているかを2次元で考えてみます。
下の図の赤い四角が直方体だと思ってください。赤は流出が発生する面です。
直方体を2個並べました。両者が接する面は流出が相殺されます。黒い線が相殺される面です。
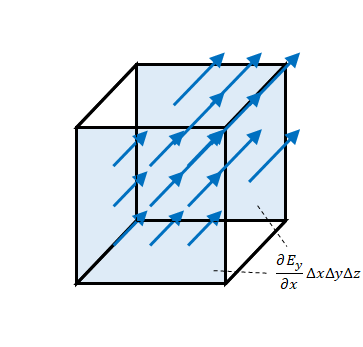
直方体の数を増やしました。周辺の赤い面からのみ流出・流入があります。
下の図は直方体を無限に小さくし、無数の直方体が並んだ状態です。
これが表面におけるベクトル場（この場合電場）の面積分であると考えることができます。
一方、面積分の元となったのは直方体の流出量ですが、これはベクトル場の発散でもあります。上記のように領域全体の和を求めるということは発散の体積積分を求めていることになります。
以上より表面におけるベクトル場の面積分と領域内の発散が等しいこと、つまりガウスの法則が正しいことが確認できました。
4.3 電荷から離れたところに電場が発生することが微分形より示される？
発散定理について補足します。
積分形によれば、領域内のどこに電荷があっても境界には電場が発生しています。
一方、微分形からわかるのは、正の点電荷が一つあったとすると、その点における発散のみが正になり、周辺の発散は全て0ということです。
法則通りであれば、直感的には点電荷から離れたところでは電場が0になるように思えます。
微分形で、点電荷の大きさが、離れた点の電場に反映されるのでしょうか。
改めて小さな四角で考えてみましょう。前節は各四角の発散の和が相殺されない面に注目しましたが、ここでは電場がどのように伝達するかを考えます。
ある四角の中には正の電荷があります。外へ向く電場があります。
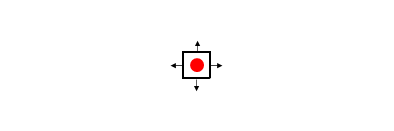
次に左隣の四角に注目します。ここには電荷はありません。この四角の電場の発散は0です。しかし右隣りとの境界よりこちらを向く電場があります。
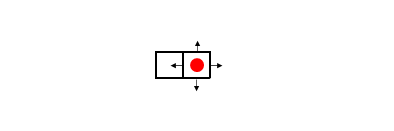
発散が0になるよう、左側の境界から外へ向く電場がなければなりません。
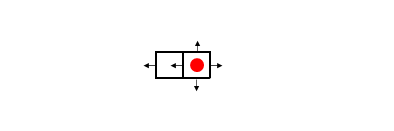
同じようにさらに左隣の四角も発散が0なので左側境界から外へ向く電場があります。
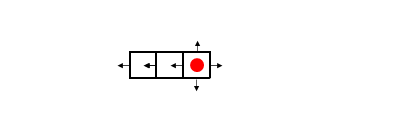
このようにして、電荷がないところでは発散が0になるよう、電場を伝達させます。
つまり、点電荷から離れた場所であっても電場は生じています。
電磁気学には「近接作用」と「遠隔作用」という言葉があります。
近接作用というのは、ある事象が隣接する場所に影響を及ぼすことにより連鎖的に周囲へ波及するという考え方です。
遠隔作用は、離れている2点間で直接作用するという考え方です。
微分系の場合、点電荷から離れたところに電場が生じることは近接作用によって説明が可能です。
5 係数と単位系
5.1 左辺と右辺の間には係数が必要ではない？
ガウスの法則をみて何か気になったことはないでしょうか。左辺は電場を面積分した値、右辺は電荷を体積積分した値です。異なる物理量が演算によって等しくなることを法則が示しているのはわかりますが、元は違う単位です。係数は必要ないのでしょうか。
例として電気回路を考えてみましょう。抵抗の両端に電圧を印可すると一定の電流が流れます。電圧（電位）を\(V\)、電流を\(I\)、抵抗を\(R\)とすると、
$$V=IR$$
と表されます。これは\(V\)が\(1[V]\)、\(R\)が\(1[\Omega]\)のとき\(I\)は\(1[A]\)であることを示しています。この関係が成立するのはそのように単位が決められているからです。
仮の話ですが、 \(V\)が\(1[V]\)、\(R\)が\(1[\Omega]\)のとき\(I\)は\(0.5[A]\)流れるように単位を決めることができたはずです。しかし、そうすると
$$V=2IR$$
と書かなければなりません。そのようなわずらわしさがなるべくないように単位が決められています。
ガウスの法則に関しても、倍率を合わせるための係数が存在しないのは偶然ではなく、そのように単位が合わせられているからです。
5.2 係数の決定
では、どのようにして単位が決められているかを考えてみましょう。電荷・電場・誘電率はクーロンの法則とも関わるので、両者を合わせて調べます。
点電荷\(q\)が1つあるとします。
\(q=1[C]\)（クーロン）の点電荷から\(r[m]\)離れたところの電場を\(E[N/m]\)とします。\(\boldsymbol{E}\)はベクトル、\(E\)はスカラーとします。
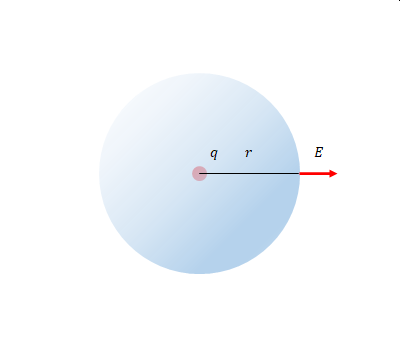
この条件およびクーロン力とクーロンの法則をガウスの法則に代入し式を変形します。途中の過程は「＋」を押して表示してください。
その結果以下となります。
$$\oint_s \boldsymbol{E} \cdot d\boldsymbol {S}= 4 \pi k \frac{1}{\epsilon_0} \int_V \rho dV$$
この\(k\)をどう決めるかという問題になります。
ガウスの法則の元の式と比べてください。\(4\pi\)はありませんね。つまり\(k=\displaystyle \frac{1}{4\pi}\)でなければなりません。
\(k= \displaystyle \frac{1}{4\pi}\)としましたが、この\(k\)はもともとクーロンの法則の係数として仮定していたものでした。MKSA単位系におけるクーロンの法則の係数は \( \displaystyle \frac{1}{4\pi}\) と決まります。5.4節を確認ください。
以上、ガウスの法則とクーロンの法則の係数が決定しました。しかし、ただ係数を決定しただけでは式が成立しません。係数を含めた式が成立するよう物理量の単位を合わせる必要があります。この単位について次節で述べます。
5.3 単位系
前節で\(k=\displaystyle \frac{1}{4\pi}\) となるよう物理量の単位を合わせていると述べました。つまり\(\boldsymbol{E}\)、\(q\)、\(\epsilon_0\)はこの式に合うように決められています。もちろんこれらの物理量はこの式だけではなく様々なところで他の物理量と関わっています。すべての関係が不自然にならないよう決める必要があります。このような複数の単位の集まりを単位系とよびます。
電磁気学で使われる単位系は1種類ではありません。複数の単位系が必要なわけではありませんが、現在のところ1種類には統一されていません。最もよく使われるのはMKSA単位系です。本サイトでここまで述べてきた内容は全てMKSA単位系を前提としています。特に断りがない限りこの後もMKSA単位系です。高校の物理でMKS単位系を習ったかもしれませんが、これに\(A\)が追加されたものです。長さは\(m\)、質量は\(kg\)、時間は\(s\)、電流は\(A\)を使用します。
\(k=\displaystyle\frac{1}{4\pi}\)となるのはMKSA単位系の場合です。他の単位系ではこの通りとは限りません。
比較のために少しだけ他の単位系ではどうなるか述べましょう。CGSガウス単位系の場合、\(k=1\)です。したがって、ガウスの法則には\(4\pi\)が出てきます。その代わりというわけでもありませんが、\(\epsilon_0=1\)となっているので式に\(\epsilon_0\)は出てきません。MKSA単位系と比べると\(4\pi\)が追加され\(\epsilon_0\)（MKSA単位系では8.85×10-12）が1になっているのでこれだけではMKSA単位系と同じように等号は成立しません。つまり等号が成立するよう\(E\)と\(q\)もMKSA単位系とは異なっています。
このようにマクスウェルの方程式に\(4\pi\)が現れる単位系と現れない単位系があります。\(4\pi\)が現れないようにすることを有理化、そのような単位系を有理単位系とよびます。無理数である\(\pi\)が現れないという意味で名付けられたようです。MKSA単位系は有理単位系です。
ところで、\(4\pi\)も\(\epsilon_0\)も現れないようにすればよいのではないでしょうか。
ガウスの法則だけを最適化するのであれば可能でしょう。しかしそうすると他の式が複雑になったり対称でなくなったりします。すべての式において係数がないようにすることはできないからこうなっているのでしょう。
また、MKSA単位系であってもクーロンの法則などには\(4\pi\)が現れます。
マクスウェルの方程式にはいろいろな意味でバリエーションがありますが、単位系によっても記述が異なります。混乱しないよう、なるべく必要な単位系のみに注目したほうがよいでしょう。
5.4 クーロンの法則
クーロンの法則はマクスウェルの方程式には直接は関係ないのですが、ガウスの法則における単位の決定（5.2節）と関りがあるので、ここで簡単に説明します。
クーロンの法則の概要は以下です。
2個の点電荷において、
・電荷にはたらく力の大きさはそれぞれの電荷の大きさに比例する。
・電荷にはたらく力の大きさは両電荷の距離の2乗の逆数に比例する。
・電荷にはたらく力の向きは両電荷を結ぶ線に沿う。ただし電荷の極性によって反転する。
\(q_1\)と\(q_2\)を点電荷、両者の距離を\(r\)、\(q_1\)から\(q_2\)へ向く単位ベクトルを\(\hat{\boldsymbol{r}}\)とします。単位ベクトルは大きさには影響がなく、向きを示すだけです。
\(q_1\) にかかる力\(\boldsymbol{F}\)は以下のように表すことができます。
$$\boldsymbol{F}=k\frac {1}{\epsilon_0} \frac {q_1 q_2 \hat{\boldsymbol{r}}}{r^2}$$
この式は最終形ではありません。\(k\)は説明のために仮に置いている係数です。単位系によって変わります。
ここでガウスの法則の表現に都合がよいよう \(k\) を決定します。5.2節に戻って確認ください。
その結果、\(k=\displaystyle \frac{1}{4\pi}\)となりました。したがって\(k\)に代入して以下のようになります。これがMKSA単位系におけるクーロンの法則です。
$$\boldsymbol{F}=\frac {1}{4\pi\epsilon_0} \frac {q_1 q_2 \hat{\boldsymbol{r}}}{r^2}$$
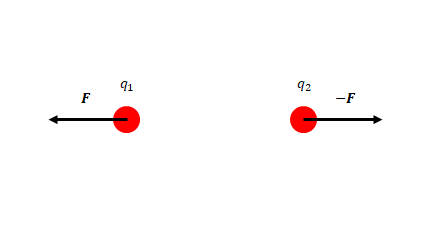
ついでに\(q_1\)と\(q_2\)の電荷の極性と力の関係を確認しましょう。
極性が異なる場合は下図のようになります。
\(q_1\)と\(q_2\)にかかる力は同じ大きさで逆向きです。
極性が同じ場合は互いに反発します。
ここまで述べたのは電荷に関する法則でしたが、磁荷に関しても同じように法則が存在します。
2つの磁荷を\(q_{m1}\)、\(q_{m2}\)、透磁率を\(\mu_0\)とすると、力は以下で表されます。
$$\boldsymbol{F}=\frac {1}{4\pi\mu_0} \frac {q_{m1} q_{m2} \hat{\boldsymbol{r}}}{r^2}$$
ただし磁荷は存在しないのでこの法則は仮想のものとされます。
6 分極
6.1 真空では分極する？
1.3節で「誘電率によって電場の弱まり方が変わる」と述べましたが、真空でも電場が弱まるのでしょうか。
電場を弱めるのは分極があるからです。しかし真空では分極は起きません。したがって真空では電場を弱めるものはありません。
\(\epsilon_0\)が使われているので真空でも電場が弱まるようなイメージがありますが、そうではありません。本来、真空においては誘電率は意味がありません。にもかかわらず\(\epsilon_0\)が出てくるのは等式を成立させるための係数のような意味があるのでしょう（前章の通りです）。
本サイトにおけるガウスの方程式は真空のみに限定しています。多くの教科書や資料も同様です。
6.2 なぜ分極によって電場が弱まる？
前節の通り、分極は真空におけるガウスの法則とは関係ありません。しかし分極がある場合とない場合の違いを知っておいたほうがよいでしょう。また、アンペールの法則では分極が原因となる現象による項があります。そこで、ここでは分極がどのような現象であるかを簡単に説明します。
強誘電体や導体の場合は以下説明の通りではないし、様々な条件で状態は変化しますが、それらについては省略します。
さて、比較のため、まずは真空での状態です。
2つの電極が向かい合っており、それぞれ正と負に帯電し電極間に\(\boldsymbol{E}\)の電場が発生しているとします。場所（下の図の場合、上下方向）により電場は変わるのではないかと思うかもしれませんが、もし電極が無限に大きい場合は電場は一様になります。ここでは電場は一様とします。
真空の場合、電場を変化させるものはありません。
次に電極の間に絶縁体が存在するとします。
点線内が絶縁体、丸が原子または分子です。
この図ではまだ電極に電荷が発生していません。
次に電極が帯電している状態です。過渡的な状態と考えてください。
絶縁体に電場が生じています。
この電場によって絶縁体内の原子・分子の原子核が負側、電子が正側へ偏ります。その結果、それぞれの原子・分子内で正と負の電荷に分かれます。
これが現象としての分極です。
これが最終の状態ではありません。隣り合う原子・分子の正と負の電荷が中和されます。
その結果、絶縁体の両端のみ電荷が残ります。
電荷によって生じる電場を\(\displaystyle \frac{\boldsymbol{P}}{\epsilon_0}\)で表します。生じた電場は\(\boldsymbol{E}\)とは反対の向きです。
絶縁体内の電場は\(\displaystyle \frac{\boldsymbol{P}}{\epsilon_0}\)だけ弱まります。つまり電場は
$$\boldsymbol{E} – \frac{\boldsymbol{P}} {\epsilon_0}$$
となります。
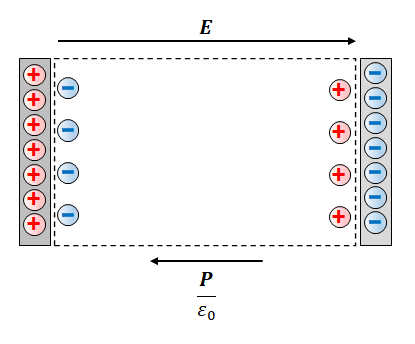
電束密度（7.1節参照）は\(\epsilon_0\)をかけて、
$$\boldsymbol{D}= \epsilon_0 \boldsymbol{E} – \boldsymbol{P}$$
と表されます。
この\(\boldsymbol{P}\)が物理量としての分極です。
電極の間に絶縁体があれば絶縁体内の電場は弱くなりますが、もし部分的に絶縁体が充填されていないところがあればそこの電場は\(\boldsymbol{E}\)のままです。
ここでは絶縁体という言葉を使いましたが、誘電体という言葉も使われます。両者が指す物質は同じですが、電場によって分極する物質という意味を込める場合は絶縁体ではなく誘電体という言葉がよく使われます。
6.3 電荷があると真空ではない？
ガウスの法則は電荷と電場の関係を示す法則です。本サイトでは真空の場合に限定しています。しかし真空とは何もない状態です。電荷があっても真空といえるのでしょうか。
本ページで想定していたのは分極のない状態です。分極があると誘電率が変わるからです（\(\epsilon_0\)を適用できなくなります）。
単極（正または負の）電荷のみが存在する状態では誘電率は真空の値のままです。
したがって、単極の電荷がいくらあってもガウスの法則は真空として成立します。
7 その他
7.1 電束・電束密度・電束線
本サイトのマクスウェル方程式はE-B対応にしたため電束密度は出てきませんが、E-H対応の場合は電束密度が出てきます。
E-B対応とE-H対応の両方を正確に知る必要はないと思います。違いさえおさえておけばE-B対応、E-H対応どちらかだけを理解すればよいでしょう。
それがE-B対応であれば電束密度は不要です。
マクスウェル方程式は電気だけではなく磁気に関しても記述があります。両者は対称な部分もありますが、異なる部分もあります。この違いを理解するために少しだけ関わってきます。そのためにここでは参考として電束密度について簡単に述べます。
さて、電束とは電荷から発する電気の流れを束に見立てたものです。電束密度は空間中の電束の密度を示します。電束もE-B対応では出てきません。
電束と電束密度の関係は電荷と電場の関係に似ています。
むしろ、電束は電荷と同じと考えてよいと思います。電束の単位は\(C\)（クーロン）です。\(1[C]\)の電荷にある電束は\(1[C]\)です。
電束密度は電場とは異なります。ただし真空中においては電束密度は電場に誘電率を掛けただけの値です。
電束密度は一般的に\(\boldsymbol{D}\)で表されます。真空では電束密度・電場・誘電率は以下の関係にあります。
$$\boldsymbol{D}=\epsilon_0 \boldsymbol{E}$$
真空においては電束密度と電場は独立した物理量というわけではありません。電場とは性質の異なる物理量が現れてやっかいだなあ、と思ったかもしれませんが、この式のように単純な関係にあることだけを理解しておけばよいと思います。
電気力線と似た概念で電束線もあります。
電気力線は\(1[C]\)の電荷に対し、\(\displaystyle \frac{1}{\epsilon}[本]\)でしたが、電束線は\(1[C]\)の電束に対し、\(1[本]\)です。
E-H対応のガウスの法則では\(\boldsymbol{E}\)を使わず\(\boldsymbol{D}\)で表します。
8 まとめ
・ガウスの法則は領域の境界における電場の和と領域内の電荷を誘電率で割った値の和が等しいことを示しています。
・微分形は微小な領域、積分は有限な領域における法則です。
・ガウスの定理（発散定理）を使うことにより微分形と積分形が等価であることが示されます。
・多くの場合、ガウスの法則における誘電率は真空の値を適用します。つまりガウスの法則は真空における現象を示しています。本サイトも真空の場合の記述を掲載しています。
・電荷の周囲に絶縁体があった場合、原子・分子の電子・原子核が偏ることにより部分的に正と負の電荷の対が生じます。これを分極とよびます。絶縁体内部の隣り合う電荷は打ち消し合いますが電極に近い面と遠い面近くに電荷が残ります。この電荷によって、分極している物質の中の電場は弱まります。ただし真空の場合は分極は発生しません。
・E-B対応では電場を使用しますが、E-H対応では電束密度を使用します。本サイトはE-B対応にて表しています。
・単位系によってマクスウェルの方程式は変わります。本サイトではMKSA単位系について述べています。