スカラー場は多変数関数であるため、この積分は高校で勉強した積分とは異なる形式が存在します。さらにベクトル場の積分はスカラー場とは異なる演算が必要になります。本ページではそれらについて説明します。
線積分と面積分の定義を、それぞれ線の長さや面積を変数とした場合と、直交座標系での場合について述べます。
0 補足と本ページの構成
0.1 リーマン和とリーマン積分
まず補足としてリーマン和とリーマン積分について簡単に説明します。難しそうですが、高校で習った積分の手順とほぼ同じです。
図のように関数\(f(x)\)があり\(x\)軸が任意の長さで区切られています。その区間内の任意の点を\(t_k(k=0,1,\dots,n)\)とします。また、各区間の幅を\(\Delta_k\)で表します。

\(f(x)\)が\(t_k\)を通るように各区間の矩形を決めその面積の和を求めたものがリーマン和です。
以下のように表されます。
$$\sum_{k=1}^{n} f(t_k)\Delta_k$$
この\(\Delta_k\)を無限に小さくするとリーマン積分になります。
$$\lim_{n \to \infty} \sum_{k=1}^{n} f(t_k)\Delta_k$$

「リーマン」と付くぐらいなので他の積分も存在しますが、ここで説明する積分は全てリーマン積分です。
高校で習ったのは下の図のような区間の長さが一定で\(f(x)\)が各区間の左端を通っていたものだと思いますが、\(t_k\)が0で\(\Delta_k\)が一定というだけでリーマン和であることに変わりはありません。それぞれの区間が無限小になれば元の\(x\)の区間が均等であってもなくても、\(t_k\)が0であってもなくても積分の結果は変わりません。

以下、グラフ上での\(\Delta\)を示してから積分を導出しているところがあります。過程の説明を省略していますが、これらはリーマン和・リーマン積分であることをご了解ください。
また、リーマン和の添え字を追加していますがその説明も省略しています。
0.2 本ページの構成
本ページの構成は以下の通りです。説明の主な目的は線積分と面積分の定義についてですが、それぞれ被積分関数がスカラー場(スカラー値関数)、ベクトル場(ベクトル値関数)の場合に分け、さらに線素/面素を使う場合と座標の変数を使う場合に分けます。線素/面素を使う場合はほぼ定義の通りですが、座標の変数を使う場合は式の変形が必要なところがありやや複雑です。
1 線積分
1.1 スカラー場の線積分
1.1.1 線素を変数として積分する場合
1.1.2 直交座標の変数で積分する場合
1.2 ベクトル場の線積分
1.2.1 線の中の位置ベクトルを変数にして積分する場合
1.2.2 直交座標の変数で積分する場合
2 面積分
2.1 スカラー場の面積分
2.1.1 面素を変数として積分する場合
2.1.2 曲面座標の変数で積分する場合
2.1.3 直交座標の変数で積分する場合
2.2 ベクトル場の面積分
2.2.1 面素を変数として積分する場合
2.2.2 曲面座標の変数で積分する場合
3 その他
3.1 スカラー場の体積積分
3.2 閉路積分
1 線積分
1.1 スカラー場の線積分
1.1.1 線素を変数として積分する場合
スカラー場の線積分とは、場に存在する線に沿って積分することです。
高校数学の積分と線積分では何が違うのでしょう。
高校数学の積分は1変数関数が対象でした。グラフ上では\(x\)軸に沿って積分をします。\(x\)軸は当然ながら直線です。
$$\int f(x) dx $$

これに対し2次元以上のスカラー場の場合、積分経路は\(x\)軸上や\(y\)軸上である必要はありません。2次元の場合、積分可能な限りにおいて\(xy\)平面上で自由に定義できます。
2次元のスカラー場(図の緑色の面)を\(f\)とします。下の図の上下方向はスカラーを示しているのであって、空間ではない点に注意ください。
さて、\(xy\)平面上に曲線\(C\)があるとします。

線微分をするためには始点と終点が決められていないといけません。図では曲線の左端が始点であったとします。始点から曲線\(C\)上の任意の点までの長さを\(s\)で表すことにします。\(C\)上のスカラーは\(f(s)\)と表されます。

次の図のように曲線\(C\)を\(n\)等分します。\(n\)を無限大にした場合、つまり区間の長さを無限小にした場合の区間を線素とよびます。
位置ベクトルを整数\(i\)を使って\(\boldsymbol{r}_i\)と表します。

スカラーは\(\boldsymbol{r}_i\)を使って\(f(\boldsymbol{r}_i)\)と表すことができます。
分けた区間の\(s\)の長さを\(s_i\)とします。

リーマン和は以下のように表されます。
$$\sum_{i=1}^{n}f(\boldsymbol{r}_i) \Delta s_i$$
リーマン積分は以下のように表されます。
$$ \lim_{n \to \infty} \sum_{i=1}^{n}f \Delta s_i = \int_C f ds $$
これが線積分です。
積分記号の右下の\(C\)は積分の経路を示しています。
下の図の青の図形の下側の曲線が積分経路、上の曲線が\(f\)です。積分で得られる値は青色の曲面の面積です。
1.1.2 直交座標の変数で積分する場合
次に2次元の線積分を\(s\)ではなく\(x\)と\(y\)で表すことを考えてみます。前項と同じ積分ではありますが、線素を使わずに座標の変数を使うという違いです。
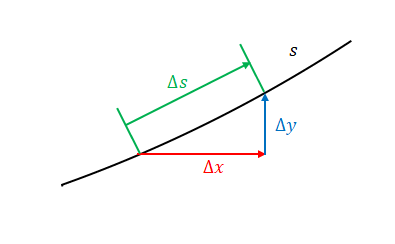
曲線\(C\)上の微小領域を\(\Delta s\)とします。
この\(x\)と\(y\)の成分を\(\Delta x\)、\(\Delta y\)とすると、
$$\Delta s = \sqrt {\Delta x^2 +\Delta y^2} $$
と表すことができます。しかし\(\Delta x\)と\(\Delta y\)の1次式ではないのでこのままリーマン和にはできません。
そこで媒介変数を使用します。媒介変数とは変数や関数の関係を表すための変数です。
\(x\)、\(y\)を\(x(t)\)、\(y(t)\)と表すことにします。\(t\)が増えると一定の割合で\(s\)が増えるよう \(x(t)\)、\(y(t)\) が定義されているものとします。この場合の媒介変数は\(t\)です。
\(x(t)\)の微小な増分を\(\Delta x\)、\(t\)の微小な増分を\(\Delta t\)とします。\(x(t)\)の傾きは\( \displaystyle \frac { dx(t)} { dt} \Delta t \)です。傾きに\(\Delta t\)を掛けているのでこれは\(\Delta x\)になります。\(y\)についても同様です。
$$\Delta x = \frac { dx(t)} { dt} \Delta t $$
$$\Delta y = \frac { dy(t)} { dt} \Delta t $$
両者より\(\Delta s\)は以下です。
$$\Delta s = \sqrt{ \frac { d^2 x(t)}{dt^2} + \frac {d^2 y(t)}{dt^2}} \Delta t$$
リーマン和からリーマン積分にすると以下です。右辺がスカラー場の線積分です。
$$ \lim_{n \to \infty} \sum_{i=1}^{n}f(x(t_i),y_i(t_i)) \Delta s_i= \int_C f(x(t),y(t)) \sqrt{ \frac {d^2 x(t)}{dt^2} + \frac {d^2 y(t)}{dt^2}} dt $$
上の式は2次元でしたが、3次元のスカラー場であれば\(z(t)\)を追加し以下です。
$$\int_C f(x(t), y(t), z(t)) \sqrt{ \frac {d^2 x(t)}{dt^2} + \frac {d^2 y(t)}{dt^2} + \frac {d ^2 z (t)}{dt^2}} dt $$
1.2 ベクトル場の線積分
1.2.1 線の中の位置ベクトルを変数にして積分する場合
下の図のように2次元のベクトル場\(\boldsymbol{f}\)の中に曲線\(C\)があるとします。

\(\boldsymbol {r}\)は曲線\(C\)上を動く位置ベクトルです。位置ベクトルは物理量の向き・大きさを表すものではなく、ある点からの相対位置を表すためのものです。ここでは\(\boldsymbol {r} = (x, y)\)とします。

ここで、\(\boldsymbol {r} \)の微小な増分を\(\Delta \boldsymbol{r}=(\Delta x, \Delta y)\)とします。 \(\Delta \boldsymbol{r} \)を無限に小さくすると曲線\(C\)の接ベクトルとなります。接ベクトルとは曲面・曲線に接するベクトルです。

微分の定義を学習したときを思い出してください。接線は\(\Delta x\)を無限に小さくしたときの\((x, y)\)と\((x + \Delta x, y + \Delta y)\)を通る線でしたね。接ベクトルも同じで\((\Delta x)\)を無限に小さくしたときの\((x, y)\)と\((x + \Delta x, y + \Delta y)\)を通るベクトルは接ベクトルです。
ベクトル場における線積分はこの接ベクトルと(曲線\(C\)と交差する)ベクトル場の内積のリーマン積分のことです。

リーマン積分が下式です。右辺がベクトル場の線積分です。
$$\lim_{n \to \infty} \sum_{i=1}^{n}f(\boldsymbol{r}_i) \cdot \Delta \boldsymbol{r}_i = \int_C \boldsymbol {f} \cdot d\boldsymbol {r} $$
内積はスカラーなので積分で得られるのはベクトルではなくスカラーです。
例えば下の図のように曲線に直交するベクトル場であれば線積分は0です。

1.2.2 直交座標の変数で積分する場合
スカラー場の場合と同様に線積分を直交座標で表します。
スカラー場の場合は\(\Delta s\)を\(\Delta x\)、\(\Delta y\)に置き換えると簡単な式にならないので媒介変数を使用しました。しかしベクトル場の場合は \( \boldsymbol {f}\)と\( d\boldsymbol {r} \)の内積なので\(x\)と\(y\)に分けて表示することができます。
\( \boldsymbol {f}\)の\(x\)、\(y\)方向の成分をそれぞれ\(f_x\)、\(f_y\)とします。\(d\boldsymbol {r}\)の\(x\)、\(y\)方向の成分は\(dx\)、\(dy\)で表されるので、
$$\int_C \boldsymbol {f} \cdot d\boldsymbol {r} = \int_C f_x dx + \int_C f_y dy$$
となります。
3次元であれば
$$\int_C f_x dx + \int_C f_y dy + \int_C f_z dz $$
となります。
媒介変数表示を使って表す場合は以下のようになります。
\begin{eqnarray}
&& \int_C f_x((x(t),y(t),z(t)) \frac {dx(t)}{dt} dt + \\
&& \int_C f_y((x(t),y(t),z(t)) \frac {dy(t)}{dt} dt + \\
&& \int_C f_z((x(t),y(t),z(t)) \frac {dz(t)}{dt} dt
\end{eqnarray}
2 面積分
2.1 スカラー場の面積分
2.1.1 面素を変数として積分する場合
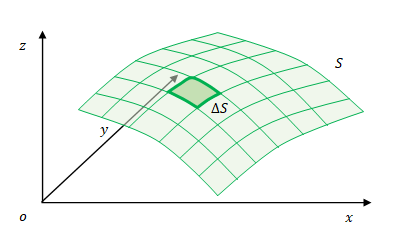
3次元のスカラー場\(f\)があり、これを面\(S\)で表すとします。

緑色の面上の各点の座標が\(f\)ではなく空間(\(z\))である点に注意ください。前述の線積分の図では上方向はスカラー場でしたが、この図の上方向は空間(\(z\))としています。スカラー場は表現していません。
面\(S\)上の微小領域を考えます。この微小領域を面素とよびます。面素を\(\Delta S\)とします。
この\(f\)と\(\Delta S \)によってリーマン積分が定義されます。右辺が面積分です。
$$\lim_{n \to \infty} \sum_{i=1}^{n} f \Delta S_i =\int_S f dS $$
\(S\)は1次元ではなく2次元 であるため、線積分とは異なるところがあります。
線積分の場合は経路が決まっていますが面積分では経路が決まっていません。 積分によって\(dS\)が面\(S\)内をくまなく移動すればその順序は関係ありません。 \(dS\)の形状も決まっているわけではありません。ただし、次節のように\(S\)を座標で表す場合は座標によって順序や形状が決まります。
2.1.2 曲面座標の変数で積分する場合
前節では面素を変数とした積分について述べましたが、ここでは座標軸で表すことを考えます。
\(xy\)平面上を動きながら積分するわけではなく、曲面\(S\)上を動きながら積分する必要があります。\(dS\)を\(dx\)、\(dy\)に変換して積分する方法がありますが、ここではそれとは別の、媒介変数を使用する方法を述べます。
下の図のように、面\(T\)上に曲面座標\(u\)、\(v\)、位置ベクトル\(\boldsymbol{r}=(x,y,z)\)があるとします。

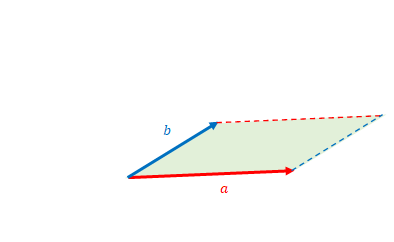
話がそれますが、外積について確認しましょう。
2本のベクトル\(a\)、\(b\)と垂直で、値が\(|a| |b| \sin \theta\)のベクトルが外積です。 \(\theta\)は図のように\(b\)が\(a\)より反時計回りに進んだ角度です。交換法則は成立せず、この図において\(a\)と\(b\)が入れ替わった場合は外積は逆を向きます。

2本のベクトルの外積は\(||a| |b| \sin \theta\) なので両者と平行な線分により形成される 緑色の面の平行四辺形の面積になります。 この性質を覚えておいてください。
面\(T\)に戻ります。以下の微小領域の赤の部分をベクトルで表すことを考えます。

\(u\)の方向の\(\boldsymbol{r}\)の傾きは\(\displaystyle\frac{\partial {\boldsymbol {r}}} {\partial u} \)です。これに\(\Delta u\)を掛けると赤の部分になります。
単に\(\Delta u\)ではいけないのでしょうか。
\(u\)はスカラーです。\(\Delta u\)もスカラーです。しかしここでは向きを伴う演算が必要です。つまりベクトルとして表す必要があります。\(\displaystyle \frac{\partial {\boldsymbol {r}}} {\partial u} \)は傾きをベクトルで表しています。これに\(\Delta u\)を掛けることにより方向と大きさの意味をもちます。
同様に青色の部分は\(\displaystyle\frac{\partial {\boldsymbol {r}}} {\partial v} \Delta v\)です。
さて、さらに両者の外積を求め、その絶対値を求めます(下記)。
$$ \left| \frac{\partial {\boldsymbol {r}}} {\partial u} \Delta u\times \frac{\partial {\boldsymbol {r}}} {\partial v} \Delta v\right|$$
なぜせっかく偏微分と外積によって得たベクトルの絶対値を求めるのでしょう。
前述の通り、外積によってその大きさは\(\displaystyle\frac{\partial {\boldsymbol {r}}} {\partial u} \Delta u\) と \(\displaystyle\frac{\partial {\boldsymbol {r}}} {\partial v} \Delta v\) および平行な線分とで作られる平行四辺形の面積になります。つまり\(\Delta S\)になるからです。
もっと簡単な方法がありそうですが、ベクトル場の面積分で似た方法を用いるので、スカラー場でもこの方法を覚えるのが良いと思います。
これから積分の式を求めると以下になります。右辺が面積分です。
$$ \lim_{n,m \to \infty} \sum_{i=1}^{n} \sum_{j=1}^{m} f (\boldsymbol{r}_{ij}) \left| \frac{\partial {\boldsymbol {r}_{ij}}} {\partial u} \Delta u_{ij}\times \frac{\partial {\boldsymbol {r}_{ij}}} {\partial v} \Delta v_{ij} \right| = \iint_T f(\boldsymbol{r}) \left| \frac {\partial \boldsymbol {r}} {\partial u} \times \frac {\partial \boldsymbol {r}} {\partial v} \right| du dv$$
\(\displaystyle \iint_T\)は2重積分です。
2.1.3 直交座標の変数で積分する場合
前節では曲面上に座標を設け、それを変数として積分しました。
曲面座標を使わずに積分する方法もあります。
図のように3次元のスカラー場の中に面\(T\)があります。面\(T\)上の位置ベクトルを\(\boldsymbol {r}\)とします。

この中の微小領域の2辺についてベクトルを\(x\)と\(y\)で表すことを考えます。
赤のベクトルは\(x\)方向に1増えると\(z\)方向に\( \displaystyle \frac{\partial {\boldsymbol {r}}} {\partial x}\)だけ増えます。
青のベクトルも同様です。

この外積の絶対値を求めます。
各ベクトルを成分表示すると \(\left(\Delta x,0, \displaystyle \frac {\partial \boldsymbol {r}} {\partial x} \Delta x \right) \)、 \( \left(0,\Delta y, \displaystyle \frac {\partial \boldsymbol {r}} {\partial y} \Delta y \right) \) となります。
\(\boldsymbol{a}=(a_x,a_y,a_z)\)、\(\boldsymbol{b}=(b_x,b_y,b_z)\) とすると、
$$\boldsymbol{a}\times\boldsymbol{b}=(a_y b_z – a_z b_y, a_z b_x – a_x b_z, a_x b_y – a_y b_x) $$
なので、
\begin{eqnarray}
&& \left|\left(\Delta x,0, \frac {\partial \boldsymbol {r}} {\partial x} \Delta x\right) \times \left(0,\Delta y, \frac {\partial \boldsymbol {r}} {\partial y} \Delta y \right) \right| \\
&=&\sqrt{{\left(\frac {\partial \boldsymbol {r}} {\partial x}\right)}^2 + {\left(\frac {\partial \boldsymbol {r}} {\partial y}\right)}^2 + 1}\Delta x \Delta y
\end{eqnarray}
です。
これよりリーマン積分は以下になります。右辺が面積分です。
\begin{eqnarray}
&& \lim_{n,m \to \infty} \sum_{i=1}^{n} \sum_{j=1}^{m} f (\boldsymbol{r}_{ij}) \sqrt{{\left(\frac {\partial \boldsymbol {r}_{ij}} {\partial x}\right)}^2 + {\left(\frac {\partial \boldsymbol {r}_{ij}} {\partial y}\right)}^2 + 1} \Delta x_{ij} \Delta y_{ij} \\
&=& \iint_T f(\boldsymbol{r}) \sqrt{{\left(\frac {\partial \boldsymbol {r}} {\partial x}\right)}^2 + {\left(\frac {\partial \boldsymbol {r}} {\partial y}\right)}^2 + 1} dx dy
\end{eqnarray}
2.2 ベクトル場の面積分
3次元のベクトル場の中に面\(S\)があるとします。

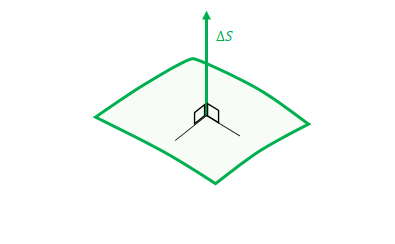
スカラー場の面積分と同じように曲面\(S\)上の微小領域を考えます。ただしスカラー場の場合とは異なり、微小領域をベクトルで表します。これを\(\Delta \boldsymbol {S}\)とします。
ベクトル場の線積分の場合も微小な増分をベクトルにしていました。しかし線積分の場合は接ベクトルであったのに対し、面積分の場合は法線ベクトルであるところが異なります。
図のように微小領域を平面とみなし、その平面上の2本に対し垂直であるベクトルが法線ベクトルです。 垂直な方向というだけでは2通りありますが、そのどちらになるかは都度定義する必要があります。あるいは後述のように曲面座標で表す場合であればそれらの方向によって決まります。
法線ベクトルとベクトル場の内積の積分がベクトル場の面積分です。

$$\lim_{n \to \infty} \sum_{i=1}^{n} \boldsymbol{f}\cdot \Delta \boldsymbol{S}_i = \int_S \boldsymbol {f} \cdot d \boldsymbol{S} $$
ベクトルの内積を積分するので結果はスカラーになります。
単位法線ベクトル(大きさが1の法線ベクトル)を\(\boldsymbol{n}\)とすると、以下のように表すこともできます(上の式と同じ結果になります)。
$$\int_S \boldsymbol {f} \cdot \boldsymbol{n} dS $$
前述の通り、線積分の場合はベクトル場と接ベクトルの内積であるのに対し、面積分の場合は法線ベクトルとの内積である点に注意してください。
2.2.1 曲面座標の変数で積分する場合
前節では\(d \boldsymbol{S}\)によって面積分を定義しましたが、次にこれを面\(T\)上の座標\(u\)、\(v\)で表します。
\(\boldsymbol{r}\)は位置ベクトルです。
2.1.2節(スカラー場の面積分)では\( \displaystyle \frac {\partial \boldsymbol {r}} {\partial u} \times \frac {\partial \boldsymbol {r}} {\partial u} \)の絶対値の積分をしましたがベクトル場の面積分の場合は絶対値にはしません。つまり外積はベクトルのまま積分します。
下の図のように\(\Delta u\)と\(\Delta v\)があるとすれば \( \displaystyle \frac {\partial \boldsymbol {r}} {\partial u} \Delta u \times \frac {\partial \boldsymbol {r}} {\partial v} \Delta v \) の大きさがこの平行四辺形の面積です。これはスカラー場の場合と同じです。
\( \displaystyle \frac {\partial \boldsymbol {r}} {\partial u} \)は面\(T\)の接線と同じ向きです。\( \displaystyle \frac {\partial \boldsymbol {r}} {\partial v} \)も同様です。外積によって得られるベクトルは2本のベクトルと垂直の向きです。つまり\( \displaystyle \frac {\partial \boldsymbol {r}} {\partial u} \Delta u \times \displaystyle \frac {\partial \boldsymbol {r}} {\partial v} \Delta v\)は面\(T\)の法線ベクトルです。
図では\(\Delta \boldsymbol{S}\)を領域の角にあるように描いていますが微小領域であるため前節のように中央にあると考えても結果は同じです。

面積分は以下のように表されます。
$$ \lim_{n,m \to \infty} \sum_{i=1}^{n} \sum_{j=1}^{m} \boldsymbol{f} \left(\boldsymbol{r}_{ij}\right) \cdot \left( \frac{\partial {\boldsymbol {r}_{ij}}} {\partial u} \Delta u_{ij}\times \frac{\partial {\boldsymbol {r}_{ij}}} {\partial v} \Delta v_{ij} \right) = \iint_T \boldsymbol{f}\left(\boldsymbol{r}\right) \cdot \left( \frac {\partial \boldsymbol {r}} {\partial u} \times \frac {\partial \boldsymbol {r}} {\partial v} \right) du dv$$
3 その他
3.1 スカラー場の体積積分
線積分や面積分と同様に体積積分も定義できます。
立体の体積を\(V\)、微小領域(直方体)を\(\Delta V\)とすると、

$$\lim_{n \to \infty }\sum_{i=1}^{n} f \Delta V_i = \int_V f dV $$
直交座標を変数とすると、

$$\iiint_D f\left(\boldsymbol{r}\right) dx dy dz $$
と表すことができます。
この座標を変数とする積分は高校数学で勉強した方法の応用かもしれません。\(f=1\)とすれば球や三角錐などの体積を求める式と同じですね。
体積積分における座標を変数とした場合は線積分や面積分に比べると簡単に演算できます。なぜ簡単なのかは省略します。
ベクトル場についても省略します。
3.2 閉路積分
2章で説明した線積分は始点と終点の位置関係については制約がありませんでした。当然始点と終点は同じ位置である必要はありませんが、逆に始点と終点が同一の位置であってもかまいません。このような積分を閉路積分または周回積分とよびます。記号は\(\displaystyle \oint\)を使います。

閉路積分であるからその結果が0になるわけではありません。0になることもありますが、それは閉路積分だからではありません。下の図の場合は正になります(上を正とした場合です)。

コーシーの積分定理では閉路積分が0になるとしていますが、これは複素積分の場合です。スカラー場やベクトル場の線積分と似ていますが定義が異なります。
面積分においても面が完全に閉じている場合は閉路積分または周回積分とよびます。
4 まとめ
4.1 スカラー場の線積分
線の長さを変数とした場合
$$\int_C f ds $$
座標を変数とした場合
$$\int_C f(x(t),y(t)) \sqrt{ \frac {d^2 x(t)}{dt^2} + \frac {d^2 y(t)}{dt^2}} dt $$
4.2 ベクトル場の線積分
線上の位置ベクトルを変数とした場合
$$ \int_C \boldsymbol {f} \cdot d\boldsymbol {r} $$
座標を変数とした場合
$$\int_C f_x dx + \int_C f_y dy$$
4.3 スカラー場の面積分
面積を変数とした場合
$$\int_S f dS $$
曲面座標を変数とした場合
$$\iint_T f(\boldsymbol{r}) \left| \frac {\partial \boldsymbol {r}} {\partial u} \times \frac {\partial \boldsymbol {r}} {\partial v} \right| du dv$$
直交座標を変数とした場合
$$ \iint_T f(\boldsymbol{r}) \sqrt{{\left(\frac {\partial \boldsymbol {r}} {\partial x}\right)}^2 + {\left(\frac {\partial \boldsymbol {r}} {\partial y}\right)}^2 + 1} dx dy$$
4.4 ベクトル場の面積分
面積を変数とした場合
$$\int_S \boldsymbol {f} \cdot d\boldsymbol{S} $$
曲面座標を変数とした場合
$$\iint_T \boldsymbol{f}\left(\boldsymbol{r}\right) \cdot \left( \frac {\partial \boldsymbol {r}} {\partial u} \times \frac {\partial \boldsymbol {r}} {\partial v} \right) du dv$$
4.5 スカラー場の体積積分
体積を変数とした場合
$$ \int_V f dV $$
直交座標を変数とした場合
$$\iiint_D f\left(\boldsymbol{r}\right) dx dy dz $$
