このページではマクスウェルの方程式の残り1つであるアンペール – マクスウェルの式について説明します。 マクスウェル – ファラデーの式の場合と共通の概念については省略します。アンペールが発見した部分とマクスウェルが追加した部分があるので分けて述べます。
微分形
$$ \nabla \times \boldsymbol{B} = \mu_0 \left( \boldsymbol {J} + \epsilon_0 \frac {\partial \boldsymbol {E} } { \partial t} \right) $$
積分形
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 \left( \int_S \boldsymbol{J} \cdot d\boldsymbol{S} + \epsilon_0 \frac{d}{dt} \int_S \boldsymbol{E} \cdot d\boldsymbol{S} \right)$$
0 名称と適用範囲
本ページでの名称と適用範囲について述べます。本ページ固有のものもありますのでご注意ください。
0.1 アンペールの法則
変位電流による項を除外した式(右辺は第1項のみの式)はコンデンサ以外の回路における電流と周辺の磁場に関する法則を示しています。一般的には「アンペールの法則」とよばれます。これとは別に電流と力の関係を示したものをアンペールの法則とよぶ場合がありますが、本ページでは前者をアンペールの法則とよびます。後者については言及しません。
0.2 変位電流追加
本ページの微分形・積分形の右辺第2項はマクスウェルが追加した、「変位電流」を考慮したものです。本ページではこれを含めた(冒頭の)式を「アンペール – マクスウェルの式」とよびます。本ページの目的であるマクスウェルの方程式はこのアンペール – マクスウェルの式を指します。
冒頭の微分形・積分形の右辺の第2項は「変位電流による項」とよぶことにします。
0.3 本ページの構成
以下の構成です。
1 アンペールの法則
2 変位電流
3 まとめ
1 アンペールの法則
本章では3通りの記述形式によるアンペールの法則の記述形式について説明します。
1.1 電流と磁場の関係
電流と周辺の磁場の関係で表した場合です。
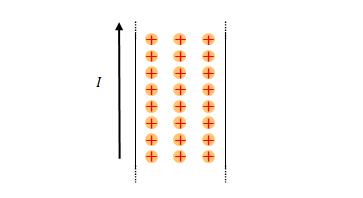
図のように無限長かつ直線の導線に一定の電流\(I\)が流れているとします。導線より\(r\)離れたところにおける磁場を\(H\)とすると、

$$2\pi r H= I$$
の関係にあります。磁場\(B\)を用いて表すと、
$$2\pi r B= \mu_0 I$$
です。
1.2 アンペール – マクスウェルの式(微分形)
アンペール – マクスウェルの式の微分形より変位電流の項を除外した場合です(下記)。
$$ \nabla \times \boldsymbol{B} = \mu_0 \boldsymbol {J} $$
電流ではなく電流密度が使われています。電流の流れ(電荷の流れ)に垂直な面を\(S\)とすると、電流密度は以下の関係です。
$$ I=\int_S \boldsymbol{J} \cdot d \boldsymbol{S}$$
アンペール – マクスウェルの式は図のイメージです。
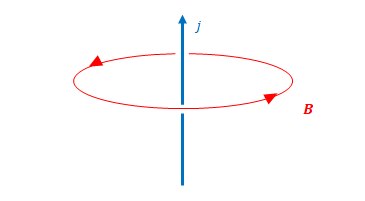
1.3 アンペール・マクスウェルの式(積分形)
アンペール – マクスウェルの式の積分形より変位電流の項を除外した場合です。
マクスウェル – ファラデーの式の場合と同様、微分形を面積分しストークスの定理を適用することにより、
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 \int_S \boldsymbol{J} \cdot d\boldsymbol{S}$$
が得られます。
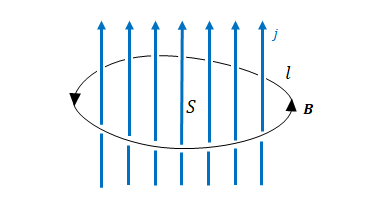
また、曲面\(S\)を半径\(r\)の円とし、その中心のみに電流\(I = \displaystyle f\int_S \boldsymbol {J} \cdot d \boldsymbol{S}\)があるとすると、積分形の
右辺は
$$ 2\pi r B$$
左辺は
$$\mu_0 I $$
となり1.1節の式と一致します。
なお、以下はアンペールの周回積分の法則とよばれます。
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 I$$
2 変位電流
前章で3通りの式を紹介しましたが、いずれもアンペールが発見した法則と等しいものです。
後年、マクスウェルが右辺に項を追加しました。これは「変位電流」とよばれる電流によるものです。
コンデンサがない回路では変位電流は発生せず、前章のように変位電流による項がなくても成立します。コンデンサがある場合は変位電流が発生し、項の追加が必要とされます。
2.1 電荷と電流の関係
電流は電荷と密接な関係があります。まずこの関係を確認しましょう。
2.1.1 電荷の動きと電流
図のような回路の導線(破線部分)の中について考えます。電源は下が正である点に注意ください。
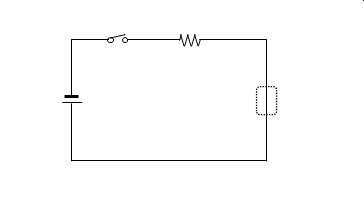
次の図は破線の部分を拡大した状態です。「+」は原子核、「ー」は電子です。電源は接続されていません。正と負の電荷の移動はありません。

電源が接続されました。導線の上側は電源の負側、導線の下側は電源の正側に接続されます。図の下端に注目してください。電子が下に向かって移動します。電子があったところが欠けた状態になります。

この原子より上にある原子の電子が、下の空いている原子へ移動します。
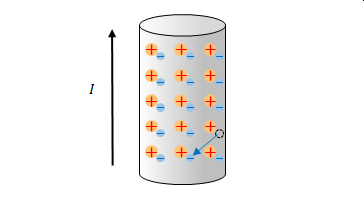
同じような動きが一斉に生じます。
つまり、電源の電位差によって負の電荷である電子が上から下へ向かって流れます。正の電荷である原子核はほとんど動かないのですが、見かけ上、正の電荷が下から上に向かって流れることと同じです。電流はこの正の電荷の流れを示しています。
※電子の動きの説明は、電流の成り立ちを理解する目的のために簡略化しています。
2.1.2 電荷の動く量と電流値の関係
電流は単位時間の間に面を通った電荷の量として規定されます。
式では
$$I=\frac{dQ}{dt}$$
と表されます。
\(dQ\)がイメージできるでしょうか。以下のように解釈しましょう。
図は導線を横から見たところです。正の電荷が下から上に流れています。
断面\(S\)を通った電荷の量を\(Q\)とします。時刻\(0\)において\(Q=0\)であったとします。

時刻\(d t\)までに面\(S\)を通過した電荷が\(d Q\)です。
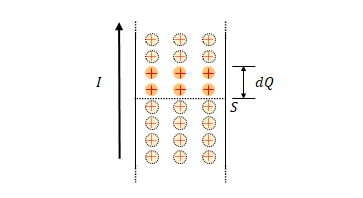
対象の面への電荷の流入量と面からの流出量の差分を\(Q\)とすると常に0になってしまいます。そうではなく、\(Q\)は対象の時間内に面を通った電荷の総量と考えます。つまり、\(Q\)は時間とともに大きくなっていきます(電荷が正で移動方向も正の場合)。\(dQ\)はその\(Q\)が\(dt\)の間に変化した量とします。
2.2 コンデンサ(キャパシタ)
変位電流は電荷の移動ではなく、コンデンサ(キャパシタ)内の電束密度の変化によって生じます。コンデンサの動きについておさらいしましょう。
コンデンサは蓄電器とよばれることからもわかるように、電気(電荷)を蓄える素子です。電荷を蓄える能力はキャパシタンス(容量)とよばれます。
キャパシタンスを\(C\)、蓄えられた電荷を\(Q\)、電極間の電圧を\(V\)とすると以下の関係にあります。つまり、電荷の量は電圧とキャパシンタンスに比例します。
$$Q=CV$$
以下のような回路で考えてみます。前節の例より電源の正と負を逆にしています。
コンデンサを拡大します。コンデンサには電源が接続されていません。
電源が接続されました。上が正、下が負に接続されます。正の電荷がコンデンサの電極に移動します。正の電荷が移動するということは負の電荷が反対の方向へ移動するということでもあります。この図では両者を描いています。
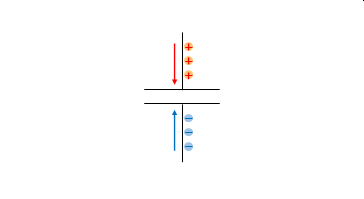
電極に電荷が蓄えられます。前述の通り、キャパシタンスと電圧によって決まる電荷の量だけ蓄えられるとそれ以上、電荷が移動することはありません。
この状態で回路を切断してもコンデンサは電荷を保持し続けます。
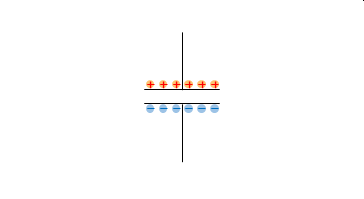
もし、両電極(または導線)を(抵抗を介して)接続すると、電極の電荷がなくなるまで逆方向に流れます。
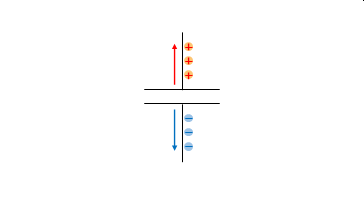
コンデンサに接続される回路の電流は定常状態では流れません。電圧が変化したときのみ流れ、電荷が飽和状態になると電流は流れなくなります。この電流が後述の変位電流です。
2.3 コンデンサにおける矛盾点
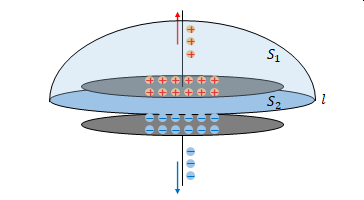
下図のようにコンデンサに電荷が蓄積された状態で導線を抵抗を介し接続し、電荷が抜けていく瞬間について考えます。電荷が増える過程ではなく、減る過程である点に注意ください。

図のように上側の電極の周囲に面\(S_1\)、面\(S_2\)があるものとします。
アンペール・マクスウェルの積分形を使用します(下記)。
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 \int_S \boldsymbol{J} \cdot d\boldsymbol{S}$$
これを\(S_1\)、\(S_2\)に適用します。
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 \int_{S1} \boldsymbol{J_1} \cdot d\boldsymbol{S}$$
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 \int_{S2} \boldsymbol{J_2} \cdot d\boldsymbol{S}$$
\(S_1\)には導線が通っており電流が流れています。これを\(I_c\)とすると、
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 I_c$$
\(S_2\)は電極の間にあります。電極の間は電荷が流れません。したがって、
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} =0$$
です。
上2式の左辺は同じなので右辺も等しいはずです。しかしそうであれば、
$$\mu_0 I_c = 0 $$
となってしまいます。
マクスウェルはこれを矛盾と考えました。
整理しましょう。
上の式の左辺は面\(S_1\)を貫く電流、つまり導線を流れる電流です。蓄積された電荷が放出されるので、その移動によって電流は流れるはずなので0ではありません(\(I_c\)としました)。
右辺は\(S_2\)を貫く電流、つまりコンデンサの内部を流れる電流です。コンデンサの内部には電流は流れないので0になるはずです。
しかし、両者は境界の線\(l\)を共通にしているので、アンペールの法則より、その値が等しくならないといけないという制約があるはずなのです。
2.4 変位電流
マクスウェルはこの矛盾を解消するため、コンデンサの中に流れる電流を考えました。導線や抵抗を流れる電流は電荷の移動によるものですが、コンデンサの中では電荷の移動はありません。しかしコンデンサの電極に蓄積されている電荷が変化すると電束密度も変化し、この電束密度の変化を電流とみなすことにしました。これが「変位電流」です。
変位電流の項が定義通りであることを確認しましょう。
前節の矛盾がないようにするためには変位電流が導線に流れる電流と等しくなければなりません。そこで\(I_c = I_d\)(下図)と仮定し、変位電流密度(変位電流の電流密度)と電場の時間変化の関係を求めます。
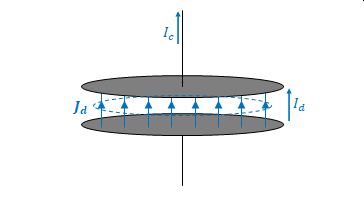
改めて、コンデンサと面\(S_1\)、面\(S_2\)の図です。電極の間の電場を\(\boldsymbol{E}\)、両電極の電荷を\(+Q\)、\(-Q\)、電極間を流れる電流を\(I_d\)、電流密度を\(J_d\)とします。
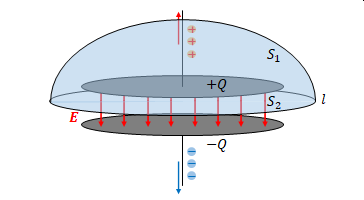
(1)ガウスの法則
\(\boldsymbol {E}\)を面\(S_1 + S_2\)で面積分します。
ガウスの法則より、
$$ \oint_{S_1 + S_2} \boldsymbol{E} \cdot d\boldsymbol {S} = \frac{1}{\epsilon_0} \int_V \rho dV$$
\(\rho\)は電荷密度なので体積積分にするとQです。また、\(\epsilon_0\)を左辺に移動します。
$$ \oint_{S_1 + S_2} \epsilon_0 \boldsymbol{E} \cdot d\boldsymbol {S} = Q$$
(2)\(S_1\)の削除
面\(S_1\)はコンデンサの外なので\(\boldsymbol{E}\)はありません。
$$\int_{S_1} \boldsymbol{E} \cdot d \boldsymbol {S} = 0$$
したがって、
$$ \int_{S_1 + S_2} \boldsymbol{E} \cdot d \boldsymbol {S} = \int_{S_2} \boldsymbol{E} \cdot d \boldsymbol {S} $$
です。
(3)時間微分
上記(1)と(2)より、
$$ \int_{S_2} \boldsymbol{E} \cdot d \boldsymbol {S} = \frac{Q}{\epsilon_0}$$
\(\epsilon_0\)を移動し、
$$ \int_{S_2} \epsilon_0 \boldsymbol{E} \cdot d \boldsymbol {S} = Q$$
両辺を時間に関し微分すると、
$$ \frac{d}{dt} \int_{S_2} \epsilon_0 \boldsymbol{E} \cdot d \boldsymbol {S} = \frac{dQ}{dt} $$
(4)右辺の電荷の時間微分を電流密度に変換
左辺は微分と積分の順序を入れ替えます。右辺は\(I_d=\displaystyle \frac{d}{dt}Q\)を適用します(時間\(dt\)の間に閉面\(S_1 + S_2\)より流出する電荷の量です)。
$$ \oint_{S_1 + S_2} \epsilon_0 \frac{\partial \boldsymbol{E}}{\partial t} \cdot d\boldsymbol {S} = I_d$$
電流を電流密度に置き換えます。
$$ \oint_{S_1 + S_2} \epsilon_0 \frac{\partial \boldsymbol{E}}{\partial t} \cdot d\boldsymbol {S} = \oint_{S_1 + S_2} \boldsymbol{J_d} \cdot d \boldsymbol {S}$$
(5)両辺の被積分関数の関係
両辺の積分の範囲が等しいので積分関数が等しいといえます。したがって、
$$\boldsymbol{J_d} = \epsilon_0 \frac{\partial \boldsymbol{E}}{\partial t} $$
となります。微分形における変位電流の項と同じになりました。
2.6 アンペール – マクスェルの式への適用
前節最後の右辺が微分形の右辺の第2項として追加されたものです(下記)。第1項同様、\(\boldsymbol{H}\)ではなく\(\boldsymbol{B}\)の式で表すために\(\mu_0\)が追加されています。
$$ \nabla \times \boldsymbol{B} = \mu_0 \left( \boldsymbol {J} + \epsilon_0 \frac {\partial \boldsymbol {E} } { \partial t} \right) $$
微分形の右辺第2項を面積分し微分と積分を入れ替えることで積分形の第2項に対応します。
$$ \oint_l \boldsymbol{B} \cdot d\boldsymbol {l} = \mu_0 \left( \int_S \boldsymbol{J} \cdot d\boldsymbol{S} + \epsilon_0 \frac{d}{dt} \int_S \boldsymbol{E} \cdot d\boldsymbol{S} \right)$$
定常電流密度と変位電流密度の和となっています。これはどう考えればよいでしょう。
積分形は連続的に広がっている電流密度に対して定義されています。これは複数の経路があるような場合も考えられます。領域内のある経路はコンデンサがなく(定常電流密度)、ある経路はコンデンサがあった(変位電流密度)としてもそれぞれの電流密度の和として表されます。
微分形は1点で定義されます。コンデンサがないか、あるかどちらかです。コンデンサがなければ右辺の第2項は0、コンデンサがあれば第1項は0と考えれば不整合はありません。
2.7 補足:抵抗の内部における電場と電流密度の関係
2.5節ではコンデンサの内部における電場と電流密度の関係を求めました。
抵抗の内部ではこのようにはなりません。以下のように表されます。
$$\boldsymbol{J}=\sigma \boldsymbol {E} $$
\(\sigma\)は電気伝導率で、抵抗値の逆数を単位長さ当たりで表したものです。
3 まとめ
・本サイトでは以下のように区別しました。
アンペールの法則:
変位電流の項を含まない
アンペール – マクスウェルの式
変位電流の項を含む
・アンペールの法則は無限の直線の導線内を流れる定常電流または定常電流密度と周辺の磁場の関係を示したものです。
・アンペール・マクスウェルの式(微分形・積分形)はアンペールの法則と比べると変位電流密度の項が追加されています。
・変位電流とは、コンデンサ内の電束密度(電場)の時間変化によって生じる電流です。コンデンサの中を電荷が移動するわけではありません。ただし、外からコンデンサの電極への電荷の蓄積や、電極から外への電荷の放出による電荷の移動があります。これは変位電流と同じ値です。
