ここまで、いくつかのページで力学に関する物理量の変換を取り上げましたが、電磁場も当然座標系によって異なります。変換の式の導出にはいくつかの方法がありますが、本ページでは電荷との関係から求めます。
1 電磁場の変換
1.1 前提条件
下の図のように3種類の座標系において、正と負の電荷を帯びている、無限大の面積の2枚の板があるところを考えます。
1つめの座標系は\(S\)です。
観測者は\(S\)に固定されています。
\(S\)で測った板の速度は\(u_0\)、板の電荷密度は\(\sigma\)と\(-\sigma\)です。
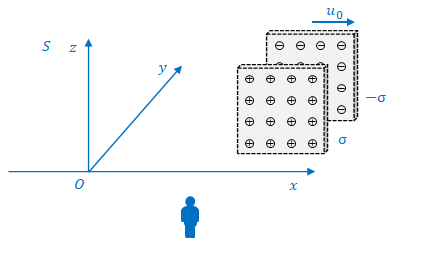
\(\sigma\)は体積密度ではなく面密度である点に注意してください。また、面密度は移動方向とは垂直な面ではなく、電荷の移動方向と平行な面(\(xz\)面)で定義しています。
2つめの座標系は\(S’\)です。
\(S\)から見ると\(S’\)の速度は\(v\)です。
\(S’\)で測った板の速度は\(u’_0\)、板の電荷密度は\(\sigma’\)と\(-\sigma’\)です。
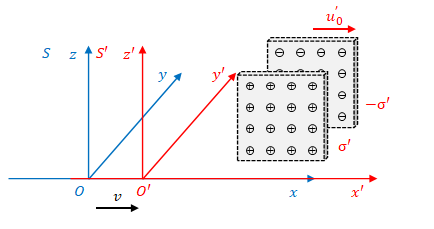
3つめの座標系は\(S_0\)です。
他の慣性系から見ると、\(S_0\)は板と同じ速度で移動します。つまり、\(S_0\)から見ると板は静止しています。
\(S\)から見ると\(S_0\)の速度は\(u_0\)です。
\(S_0\)で測った板の電荷密度は\(\sigma_0\)と\(-\sigma_0\)です。
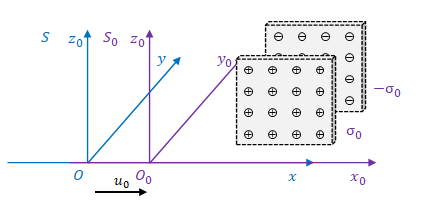
以上の条件にて次節より\(S\)と\(S’\)で測った電磁場の関係を求めます。
1.2 電荷密度の変換
\(S\)と\(S’\)で測った電荷密度つまり\(\sigma\)、\(\sigma’\)の関係を求めます。
これらの電荷密度の違いはどこからくるのでしょう。
ある領域内の電荷の総量はどの座標系で測っても同じはずです。電荷密度が変わるとすれば空間の間隔に違いがある場合です。
これがローレンツ収縮でした。
ローレンツ収縮はローレンツ因子(後述の\(\gamma\)など)によって決まります。ローレンツ因子は座標系の相対速度によって決まります。
ただしこの例の場合、電荷は\(S\)、\(S’\)どちらから見ても静止していません。そこで\(S_0\)との関係より求める必要があります。
それぞれのローレンツ因子を以下のように定義します。
$$\gamma = \sqrt{\frac{1}{1-\frac{v^2}{c^2}}} \tag{1}$$
$$\gamma_0 = \sqrt{\frac{1}{1-\frac{u_0^2}{c^2}}} \tag{2}$$
$$\gamma’_0= \sqrt{\frac{1}{1-\frac{{u’_0}’^2}{c^2}}} \tag{3}$$
座標系などとの関係は以下の通りです。
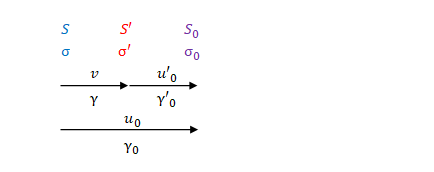
まず\( (3) \)の\(\gamma_0\)を\(u_0\)と\(v\)で表します。
速度の合成則により、
$$u_0’=\frac {u_0 – v}{1-\frac{u_0 v}{c^2}} \tag{4}$$
の関係があるのでこれを\( (3) \)に代入し2乗の逆数を計算すると、
\begin{align}
\frac{1}{{\gamma’}_0^{2}}&=1-\frac{\left(u_0-v\right)^2}{c^2\left(1-\frac{u_0v}{c^2}\right)^2}\\
&=1-\frac{u_0^2-2u_0v+v^2}{c^2-2u_0v+\frac{u_0^2v^2}{c^2}}\\
&=\frac{c^2-2u_0v+\frac{u_0^2v^2}{c^2}-u_0^2+2u_0v-v^2}{c^2-2u_0v+\frac{u_0^2v^2}{c^2}}\\
&=\frac{c^2-u_0^2-v^2+\frac{u_0^2v^2}{c^2}}{c^2-2u_0v+\frac{u_0^2v^2}{c^2}}\\
&=\frac{c^2\left(1-\frac{u_0^2}{c^2}\right)\left(1-\frac{v^2}{c^2}\right)}{c^2\left(1-\frac{u_0v}{c^2}\right)^2}\\
&=\frac{\left(1-\frac{u_0^2}{c^2}\right)\left(1-\frac{v^2}{c^2}\right)}{\left(1-\frac{u_0v}{c^2}\right)^2} \tag{5}\\
\end{align}
再び平方根の逆数にすると、
$$\gamma’_0=\frac{1-\frac{u_0v}{c^2}}{\sqrt{1-\frac{u_0^2}{c^2}}\sqrt{1-\frac{v^2}{c^2}}} \tag{6}$$
これに\( (1) \)と\( (2) \)を代入し、
$$\gamma’_0=\gamma_0\gamma\left(1-\frac{u_0v}{c^2}\right) \tag{7}$$
と表すことができます。
ローレンツ収縮はローレンツ因子によって決まります。一方、同一領域内の電荷の総量は変わらないはずです。ローレンツ収縮によって空間が収縮するほど電荷密度は大きくなるはずです。したがって以下のように表されます。
$$\sigma=\gamma_0\sigma_0 \tag{8}$$
$$\sigma’=\gamma’_0\sigma_0 \tag{9}$$
\( (9) \)に\( (8) \)を代入し、さらに\( (7) \)より、
$$\sigma’=\frac{\gamma’_0}{\gamma_0}\sigma=\gamma\sigma\left(1-\frac{u_0v}{c^2}\right) \tag{10}$$
となります。\(S\)と\(S’\)で測った電荷密度の関係が求められました。
1.4 \(S^{\prime}\)で測った\(y\)方向の電場
前節の結果を用いて、\(S’\)で測った\(y\)方向の電場\(E’_y\)(下図)
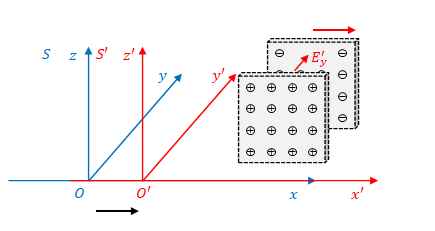
を\(S\)で測った\(y\)方向の電場\(E_y\)と\(z\)方向の磁場\(B_z\)(下図)
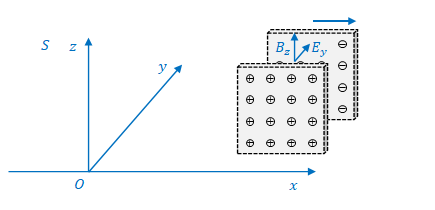
で表すことを考えます。
無限に広がる正と負に帯電した板の間の電場は、真空における誘電率\(\epsilon_0\)を用いて、
$$E_y=\frac{\sigma}{\epsilon_0} \tag{11}$$
と表すことができます(2.1節参照)。
\(S’\)座標で測った\(z\)方向の電場は、\( (11) \)と\( (10) \)を用いて、
\begin{align}
E’_y&=\frac{\sigma’}{\epsilon_0}\\
&=\frac{1}{\epsilon_0} \gamma\sigma\left(1-\frac{u_0v}{c^2}\right)\\
&=\gamma \left(\frac{\sigma}{\epsilon_0} – \frac{\sigma u_0v}{\epsilon_0 c^2}\right)\\
&=\gamma \left(E_y – \frac{\mu_0 \sigma u_0v}{\epsilon_0 \mu_0 c^2}\right)\tag{12}\\
\end{align}
ここで、
$$\epsilon_0 \mu_0 = \frac{1}{c^2}\tag{13}$$
を代入して、
\begin{align}
E’_y&=\gamma \left(E_y -\mu_0 \sigma u_0v \right)\tag{14}\\
\end{align}
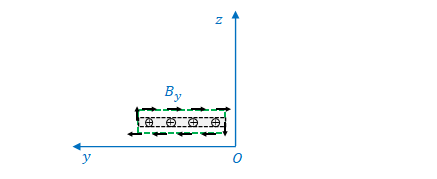
板に挟まれた空間の\(y\)方向の磁場を\(B_y\)とすると
$$B_y=\mu_0 \sigma u_0\tag{15}$$
の関係にあります(2.2節参照)。これを代入して、
$$E’_y=\gamma \left(E_y – v B_z \right)\tag{16}$$
が得られます。
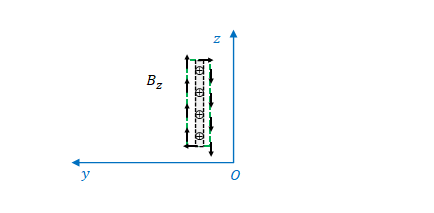
1.5 \(S^{\prime}\)で測った\(z\)方向の磁場
同様に\(B’_z\)(下図)と\(B_y\)、\(E_z\)の関係を求めます。
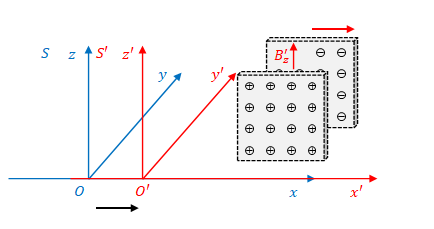
後述2.2節の\( (40) \)の通り、\(2\)枚の正負に帯電した板の間の磁場は、
$$B_z=\mu_0 \sigma u_0\tag{17}$$
です。\(S’\)においては、
$$B’_z=\mu_0 \sigma’ u’_0\tag{18}$$
ですが、これに\( (10) \)と\( (4) \)を代入し(1行目)、さらに\( (17) \)を代入し(3行目)、
\begin{align}
B’_z&=\mu_0 \gamma\sigma\left(1-\frac{u_0v}{c^2}\right) \frac {u_0 – v}{1-\frac{u_0 v}{c^2}} \\
&= \mu_0 \gamma\sigma\left(u_0 – v\right) \\
&= \gamma\left(B_y – \mu_0 \sigma v\right) \tag{19}
\end{align}
\( (11) \)と\( (13) \)を括弧内2項目に代入し、
\begin{align}
B’_z&= \gamma\left(B_z – \frac {\epsilon_0 \mu_0 \sigma v}{\epsilon_0}\right)\\
&=\gamma\left(B_z – \frac {vE_y}{c^2}\right)\tag{20}
\end{align}
以上、磁場の変換式も求められました。
1.6 \(S^{\prime}\)で測った\(z\)方向の電場と\(y\)方向の磁場
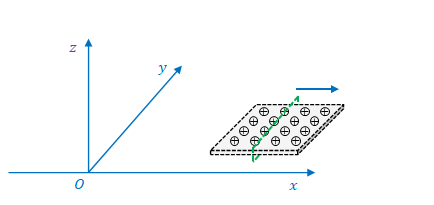
前節までは板が\(xz\)平面と平行にある場合について考えましたが、下の図のように板が\(xy\)平面と平行であるとすれば、\(E’_z\)と\(B’_y\)も同じように求めることができます。
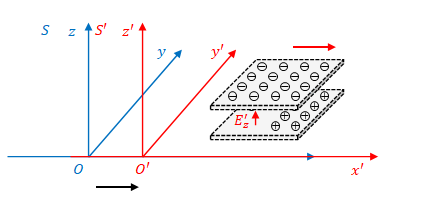
ただし、板の間にはさまれた空間の磁場は\(y\)軸の負の方を向きます。
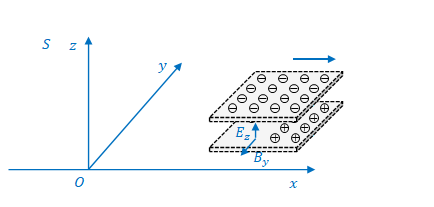
したがって前述の\( (17) \)とは異なり、
$$B_y=-\mu_0 \sigma u_0\tag{21}$$
と、負号がつきます(2.3節参照)。したがって\( (16) \)をこの条件にあてはめると、
$$E’_z=\gamma \left(E_z + v B_y \right)\tag{22}$$
と、2項目の符号が変わります。
\(B’_z\)と\(B_z\)の符号は同じです。しかし、前節と比較すると磁場と電場の符号の関係が逆になるので\( (20) \)は電場の符号を反転させ、
$$B’_y=\gamma\left(B_y + \frac {vE_z}{c^2}\right)\tag{23}$$
となります。
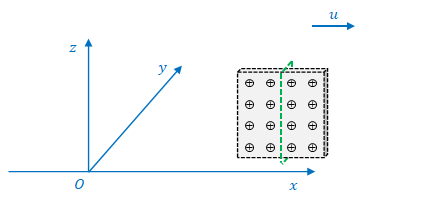
1.7 \(S^{\prime}\)で測った\(x\)方向の電場
次に\(yz\)平面に平行な板があるとし、その間の空間の電場を考えます(下図)。
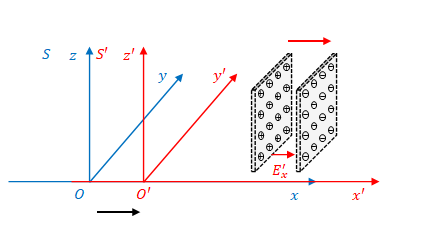
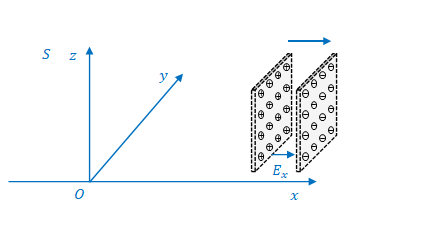
電荷密度は面積当たりの電荷の量なので、ローレンツ収縮によって\(x\)方向の間隔が変わったとしても電荷密度は変わりません。したがって、
$$E’_x=\frac{\sigma’}{\epsilon_0}=\frac{\sigma}{\epsilon_0}=E_x \tag{24}$$
となり、座標系によって\(x\)方向の電場は変わらないことがわかります。
1.8 \(S^{\prime}\)で測った\(x\)方向の磁場
最後に、板が\(xy\)平面に平行で、\(z\)方向へ移動する場合を考えます(下図)。
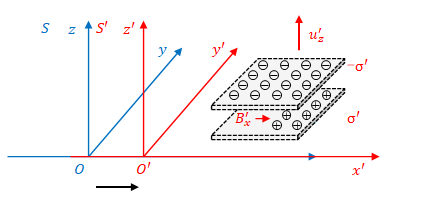
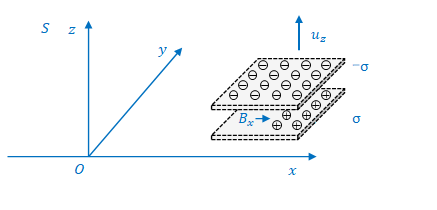
この場合、\(z\)方向に電流が流れ、その垂直方向に磁場が生じます。
板が\(x\)方向に移動しないということは、電荷密度は単にローレンツ収縮によって変化すると考えればよいので、
$$\sigma’=\gamma \sigma \tag{25}$$
となります。しかし電荷の移動速度は変化します。速度の合成則に\(v=0\)を代入して、
$$u_z’=\frac {u_z – v}{\gamma \left(1-\frac{u_z v}{c^2}\right)} =\frac {u_z }{\gamma} \tag{26}$$
の関係にあります。
磁場は電流に比例します。電流は電荷密度と(電荷の)速度に比例します。したがって相殺されて、
$$B’_x=B_x \tag{27}$$
となり、\(x\)方向の磁場も座標系によって変わりません。
以上で全方向について電磁場の変換が求められました。結果は3章を確認ください。
2 補足
2.1 帯電している板に挟まれた空間の電場
$$\int_C \boldsymbol{E} \cdot d \boldsymbol{s}= \frac{1}{\epsilon_0} \int_V \rho dV\tag{28}$$
でした。\(\rho\)は面密度ではなく体積密度である点に注意してください。
下の図のように、1枚の板を囲む直方体におけるガウスの法則を考えます。
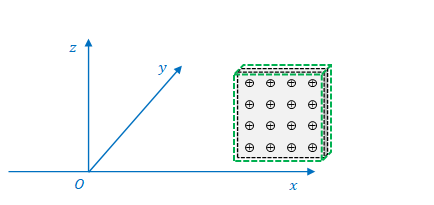
\(x\)軸の負から正に向かって見るとこのようになります。

左辺における電場を\(E_y\)とします。
\(S\)を板の面積とすれば、
$$2S E_y = \frac{S \sigma}{\epsilon_0}\tag{29}$$
ただし、板の面積を無限大としており、相対的に側面(上・下・手前・奥の面)は無視できるのでここでは含めていません。
右辺の電場は\(y\)軸の負を向いていますが、面素(\( (28) \)の\(d\boldsymbol{s}\))も負を向いているので積分は正になります。
両辺を面積で割ると、
$$E_y=\frac{\sigma}{2\epsilon_0}\tag{30}$$
となります。
ここまで、正に帯電している板周辺の電場について求めましたが、本ページの例では負に帯電している板も存在します。
これについても大きさは同じなので、板の間の電場は両者を足し、
$$E_y=\frac{\sigma}{\epsilon_0}\tag{31}$$
となります。
電場の大きさは\(2\)枚の板の距離に依存しない式になりました。これは板を無限大の面積としているからです。
2.2 帯電し、かつ移動する板に挟まれた空間の磁場(板が\(xz\)平面と平行の場合)
前節と似ていますが、ここでは移動している板を考えます。電荷が移動すると電流になり、その周囲に磁場が生じます。
この関係は以下のアンペールの法則で表すことができます。
$$\int_c \boldsymbol{B} \cdot d\boldsymbol{l}=\mu_0 I\tag{32}$$
ただし、\(\boldsymbol{B}\)は磁場、\(I\)は電流です。
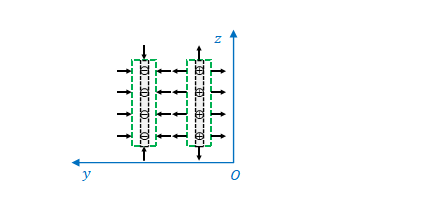
次のような正に帯電している無限に広がる板があり、速さ\(u\)で右に移動しているとします。
緑の長方形の辺についてアンペールの法則で磁場を求めます。
板を左から見ると図のようになります。左辺の磁場を\(B_z\)とします。
アンペールの法則は
$$2B_zh=\mu_0 I\tag{33}$$
と表すことができます。
\(2B_zh\)は緑の長方形の左辺と右辺に沿って積分した結果です。
右辺は磁場が\(z\)軸の負を向いていますが、この場合は時計回りに積分をするので積分の値は正です。
上辺と下辺の積分結果はここに含まれていませんが、\(h\)を無限大としているので、有限長の右辺と左辺の積分は相対的に無視できるためこの式には表れていません。
\(\Delta t\)の時間が経過する間に、下の図のように実線の位置から点線の位置まで移動し、その移動した領域の電荷を\(\Delta q\)とします(見やすくするために奥行を大きくしています)。
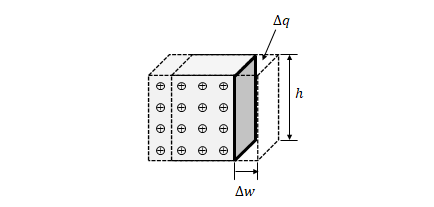
ある経路における電流は、単位時間当たりの、その経路に垂直な面を通る電荷の量として定義されます。上の図の太線で囲われた面を通る電荷の量は\(\Delta q\)なので、電流は
$$I = \frac{\Delta q} {\Delta t}\tag{34}$$
上の図のように水平方向の移動距離を\(\Delta w\)、高さを\(h\)とすると移動によってずれた面積は\(\Delta w h\)なので、電荷密度\(\sigma\)を用いて、
$$\Delta q = \Delta w h\sigma\tag{35}$$
電流は、
$$I = \frac{\Delta q} {\Delta t} = \frac {\Delta w h \sigma} {\Delta t}\tag{36}$$
板の速度は
$$u=\frac{\Delta w}{\Delta t}\tag{37}$$
なので、
$$I=h \sigma u_0\tag{38}$$
\( (33) \)に\( (38) \)を代入し、
$$B_z=\frac{\mu_0 I}{2h}=\frac{\mu_0 \sigma u_0}{2}\tag{39}$$
これが正に帯電した板の周辺の磁場です。
負に帯電した板を追加するとその間の空間の磁場は\(2\)倍になるので、

$$B_z=\mu_0 \sigma u_0\tag{40}$$
となります。
2.3 帯電し、かつ移動する板に挟まれた空間の磁場(板が\(xy\)平面と平行の場合)
下の図の緑の長方形の辺についてアンペールの法則を考えます。
\(x\)軸の負から正の方を見ると下の図のようになります。
今求めたいのは上辺の磁場です(正と負に帯電した板の間の空間だからです)。時計回りに積分すると結果は正になりますが、\(B_y\)は負です。したがって\( (33) \)をこの条件に変えると、
$$-2B_yh=\mu_0 I\tag{41}$$
と負号がつき、\( B_y \)を求める式も
$$B_y=-\mu_0 \sigma u_0\tag{42}$$
と負号がつきます。
3 まとめ
2枚の正負に帯電した板周辺の電磁場を求めることにより、以下の変換式が得られます。
\begin{align}
E’_x&=E_x\\
E’_y&=\gamma \left(E_y – v B_z \right)\\
E’_z&=\gamma \left(E_z + v B_y \right)\\
B’_x&=B_x\\
B’_y&=\gamma\left(B_y + \frac {vE_z}{c^2}\right)\\
B’_z&=\gamma\left(B_z – \frac {vE_y}{c^2}\right)
\end{align}
