アインシュタインは特殊相対性理論を導く際、以下の2つを前提として仮定しました。
・光の速度はどの慣性系から観測しても同じ。
・物理法則はどの慣性系においても同じ形式で表される。
1番目は光速度不変の原理です。既にこれまでローレンツ変換や時間の遅れなどは光速度不変の原理から導かれることをみてきました。
2番目は相対性原理(相対性理論と混同しないよう注意してください)とよばれます。これは特殊相対性理論に限ることではなく、ガリレイ変換においても同じことがいえます。
例えば、粒子の弾性衝突の前後で運動量の総和は変わりません(運動量保存則)が、これをガリレイ変換によって座標を変えてみても、それぞれの運動量は変換前とは変わりますが、運動量保存則はやはり成立します。
ローレンツ変換の場合は、運動量の定義がニュートン力学と同じままでは成立しません。本ページではその定義について考えます。
1 運動量
ニュートン力学では運動量は以下で表されました。
$$ \boldsymbol {p} = m \boldsymbol {u} $$
ただし\(m\)は質量、\(\boldsymbol {u}\)は速度です。
特殊相対性理論でも同じように表すことができるかどうかを、粒子の弾性衝突時の運動量保存則が成立するかどうかにより確認します。そして、成立しない場合、運動量の定義がどう変わるかを考えます。
1.1 特殊相対性理論における速度の合成則
図のように、3次元の座標系\(T\)と\(T’\)があるとします。\(T\)から見て\(T’\)が速度\(\boldsymbol {v} = (v,0,0)\)で移動し、粒子も\(T\)の座標では速度\(\boldsymbol{u}=(u_x, u_y, u_z)\)で移動しています。
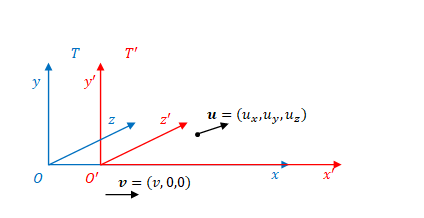
\(T’\)の座標において粒子の速度はどう表されるでしょう(観測者は\(T\)から見ているものとします)。
ローレンツ変換を使えば解決できるのでしょうか。ローレンツ変換によって変換されるのは座標であって、速度の変換を直接示しているわけではありません。しかし、ローレンツ変換は位置と時間を変換するので、これらを組み合わせれば速度を変換することができそうです。
慣性系\(T\)において、時刻\(t_0\)に粒子の位置が\( (x_0, y_0, z_0) \)、\(t_1\)に粒子の位置が\( (x_1, y_1, z_1) \)であったとします。慣性系\(T’\)の座標はローレンツ変換により
$$x’_0=\gamma (x_0 – vt) \tag{1} $$
$$t’_0=\gamma \left(t_0-\frac{v x_0}{c^2} \right) \tag{2} $$
$$x’_1=\gamma (x_1 – vt) \tag{3} $$
$$t’_1=\gamma \left(t_1-\frac{v x_1}{c^2} \right) \tag{4} $$
と表されます。
\( (3) – (1) \)より、
$$x’_1 – x’_0=\gamma \left\{ (x_1 – x_0) – v(t_1 – t_0) \right\} $$
\( (4) – (2) \)より、
$$t’_1 – t’_0 =\gamma \left\{ (t_1 – t_0) – \frac{v (x_1 – x_0) } {c^2} \right\} $$
\(x_1 – x_0\)、\(t_1 – t_0\)などが微小であるとすると、これを\(dx\)、\(dt\)などとし、
$$dx’=\gamma (dx – vdt) \tag{5} $$
$$dt’=\gamma \left(dt-\frac{v dx}{c^2} \right) \tag{6} $$
と表すことができます。
$$u’_x = \frac {dx’} {dt’} $$
を求めるため、\( (5) \)を\( (6) \)で割ります。
$$u’_x = \frac {\gamma \left( dx – v dt \right) } {\gamma \left(dt – \frac {v dx } {c^2} \right) }$$
右辺の分母と分子を\(dt\)で割り、
$$u’_x = \frac {\frac {dx} {dt} – v } {1 – \frac {v \frac {dx} {dt} } {c^2} } $$
\( \displaystyle u_x = \frac {dx} {dt}\)を代入し、
$$u’_x = \frac {u_x – v } {1 – \frac {u_x v} {c^2} } $$
\(x\)方向の変換式が得られました。
次に、同様に\(y\)方向について求めます。まず\(u’_y\)の定義は以下です。
$$u’_y = \frac {dy’} {dt’} $$
右辺の分子に\(dy’=dy\)、分母に\( (6) \)を代入し、
$$u’_y = \frac {dy } {\gamma \left( dt-\frac{v dx}{c^2} \right) }$$
右辺の分母と分子を\(dt\)で割り、
$$u’_y = \frac {\frac {dy}{dt} } {\gamma \left(1 – \frac {v \frac {dx}{dt} } {c^2} \right) } $$
\( \displaystyle u_x = \frac {dx} {dt} = u_x\)、\( \displaystyle u_y = \frac {dy} {dt} \)を代入し、
$$u’_y = \frac{u_y }{\gamma \left(1-\frac{u_x v}{c^2}\right)}$$
が得られます。
\(u’_z\)は\(u’_y\)と同様に求められます。
整理すると、
$$u’_x = \frac {u_x – v } {1 – \frac {u_x v} {c^2} } $$
$$u’_y = \frac{u_y }{\gamma \left(1-\frac{u_x v}{c^2}\right)}$$
$$u’_z = \frac{u_z }{\gamma \left(1-\frac{u_x v}{c^2}\right)}$$
ただし
$$\gamma =\frac{1} {\sqrt{1 – \frac{v^2}{c^2}}}$$
これを速度の合成則とよびます。
\(\gamma\)は物体の速度から決まる値ではなく、慣性系間の相対速度によって決まる値であることに注意してください。
1.2 ニュートン力学における運動量保存則
運動量保存則は、外部から力を加えられない状態において、物体の運動量の総和は等しいことを示しています。
粒子の弾性衝突(衝突前後で運動エネルギーの総和が同じである場合)を考えてみましょう。
ニュートン力学の場合、例えば以下のように質量\(m_a\)、\(m_b\)の粒子があり、それぞれの衝突前の速度が\(\boldsymbol{v}_{a1}\)、\(\boldsymbol{v}_{b1}\)衝突後の速度が\(\boldsymbol{v}_{a2}\)、\(\boldsymbol{v}_{b2}\)であったとすると、
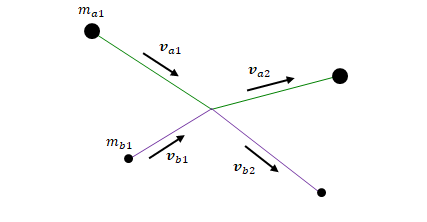
衝突前後の総運動量は以下で表されるように等しくなります。
$$m_a \boldsymbol{v}_{a1} + m_b \boldsymbol{v}_{b1} = m_a \boldsymbol{v}_{a2} + m_b \boldsymbol{v}_{b2} $$
1.3 特殊相対性理論における運動量保存則
さて、特殊相対性理論において運動量保存則が成立するかどうかを調べます。
前節と同様、粒子\(a\)と\(b\)の弾性衝突を考えます。
観測者は常に\(S\)です。\(S\)から見て\(S’\)は左へ移動しています。
まず、\(S\)が静止している座標系における粒子の運動を定義します。
\(a\)は左上から中央へ、\(b\)は右下から中央へ移動します。中央で衝突後、\(a\)は右上へ、\(b\)は左下へ移動します。粒子\(a\)と\(b\)の質量はどちらも\(m\)です。図の横方向を\(x\)、縦方向を\(y\)とします。
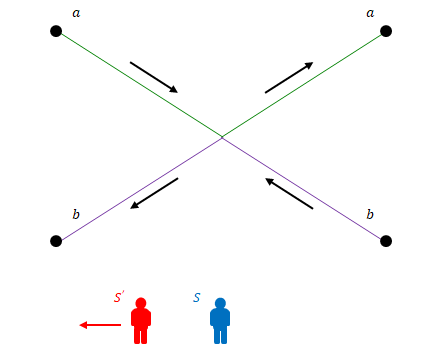
速度は以下のように定義します。粒子\(a\)と\(b\)の速度および両者の衝突前後の速度は対称です。\(S’\)は\(S\)から見て速度\( (-v_x, 0) \)で移動しています。
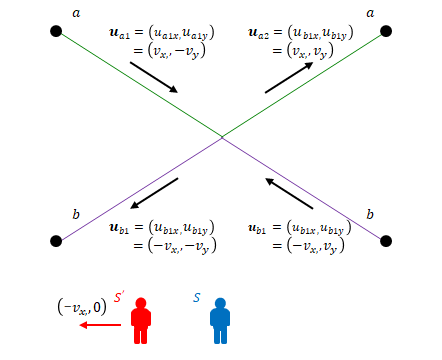
この衝突前後の粒子の速度が、\(S’\)が静止している座標ではどのように表されるかを考えます(観測者は\(S\)です)。
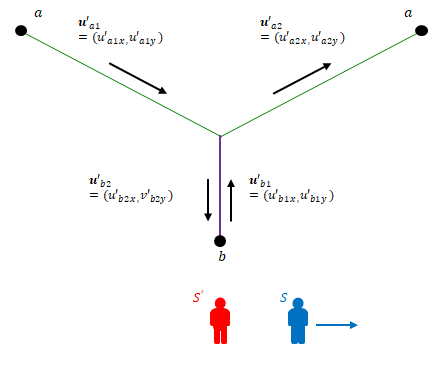
前節の速度合成則を使い、\(S’\)における\(x\)方向、\(y\)方向の速度を求めます。
\begin{eqnarray*}
u’_{a1x} &= u’_{a2x} &=\frac{2 v_x}{1+\frac{{v_x}^{2}} {c^2} }\\
-u’_{a1y} &= u’_{a2y} &= \frac{v_y \sqrt{1-\frac{v_x^2}{c^2}}}{1+\frac{{v_x}^{2}} {c^2} }\\
u’_{b1x} &= u’_{b2x} &= 0\\
u’_{b1y} &= -u’_{b2y} &= \frac{v_y \sqrt{1-\frac{v_x^2}{c^2}}}{1-\frac{{v_x}^{2}} {c^2} } &= \frac{v_y}{\sqrt{1-\frac{v_x^2}{c^2}}}
\end{eqnarray*}
これらの速度を用いて\(S’\)において運動量保存の法則が成立するかどうかを確認します。
以下の式は左辺が衝突前、右辺が衝突後です。
まず、\(x\)方向です。
$$mu’_{a1x} + mu’_{b1x} \stackrel{?}{=} mu’_{a2x} + mu’_{b2x}$$
$$m\frac{2 v_x}{1+\frac{{v_x}^{2}} {c^2} } +0 = m\frac{2 v_x}{1+\frac{{v_x}^{2}} {c^2} } +0 $$
\(x\)方向は成立することがわかります。そもそも、図からも容易に判断できます。
「\( \stackrel{?}{=} \)」は「等号が成立するかどうかはこの時点ではわからない」という意味です。
\(y\)方向はどうでしょう。
$$mu’_{a1y} + mu’_{b1y} \stackrel{?}{=} mu’_{a2y} + mu’_{b2y}$$
$$-m \frac{v_y \sqrt{1-\frac{v_x^2}{c^2}}}{ 1+\frac{{v_x}^{2}} {c^2} } + m\frac{v_y}{ \sqrt{1-\frac{v_x^2}{c^2} } }
\neq
m \frac{v_y \sqrt{1-\frac{v_x^2}{c^2}}}{1+\frac{{v_x}^{2}} {c^2} } – m\frac{v_y}{ \sqrt{1-\frac{v_x^2}{c^2} } } $$
\(y\)方向は成立しませんでした。
1.4 運動量の定義の修正
本ページ冒頭の相対性原理を思い出してください。慣性系が変わっただけで運動量保存則が成立しなくなるのは相対性原理に反します。そこで、\(S’\)においても運動量保存則が成立するよう運動量の定義を変えることを考えます。
天下り的ですが、各項に、速さによって変わる係数が付けば運動量保存則が成立すると仮定します。
そこでまず、\(u’_a=|\boldsymbol{u}’_{a1}|=|\boldsymbol{u}’_{a2}|\)、\(u’_b=|\boldsymbol{u}’_{b1}|=|\boldsymbol{u}’_{b2}|\)を定義します。さらに\(u’_a\)、\(u’_b\)によって決まる関数\(f (u’_a) \)、\(f (u’_b)\)を定義します。どのような関数であるかはこの時点ではわかりません。
そしてこれらを係数として前節の最後の式に係数として追加し、運動量保存則が成立する\(f (u’_a) \)と\(f (u’_b)\)の関係を求めます。
$$-f (u’_a) m \frac{v_y \sqrt{1-\frac{v_x^2}{c^2}}}{1+\frac{{v_x}^{2}} {c^2} } + f(u’_b) m\frac{v_y}{ \sqrt{1-\frac{v_x^2}{c^2} } } \\
= f(u’_a) m \frac{v_y \sqrt{1-\frac{v_x^2}{c^2}}}{1+\frac{{v_x}^{2}} {c^2} } – f(u’_b) m\frac{v_y}{ \sqrt{1-\frac{v_x^2}{c^2} } } \tag{7} $$
過程を省略しますが、この式より\(f(u’_a) \)と\(f(u’_b) \)の比を計算すると、
\begin{align*}
\frac {f(u’_a)} {f(u’_b)} = \frac { 1 + \frac {v_x^2} {c^2} } { 1 – \frac {v_x^2} {c^2} } \tag{8}
\end{align*}
となります。
さらに天下り的ですが、\( \displaystyle \frac {1} {\sqrt { 1 – \frac { u’^2_a} {c^2} } } \)と\( \displaystyle \frac {1} {\sqrt { 1 – \frac {u’^2_b} {c^2} } } \)の比を求めます。
過程を確認する場合は以下のリンクを開いてください。
過程を確認する場合は「+」を押して展開してください。
したがって、
以下の関係が得られました。
$$\frac { \sqrt { 1 – \frac { u’^2_b} {c^2} } } { \sqrt { 1 – \frac { u’^2_a} {c^2} } }
= \frac { 1 + \frac {v_x^2} {c^2} }{ 1 – \frac {v_x^2} {c^2} } \tag{9} $$
\( (8) \)と\( (9) \)より、
\begin{align*}
\frac { f(u’_a) } { f(u’_b) } = \frac { \sqrt { 1 – \frac { u’^2_b} {c^2} } } { \sqrt { 1 – \frac { u’^2_a} {c^2} } }
\end{align*}
\( f(u_a) \)は\(u’_a\)、\( f(u_b) \)は\(u’_b\)によって決まる値でした。したがって、
\begin{align*}
f(v’_a)=\frac{1} {\sqrt{1 – \frac{\boldsymbol{u}’^2_a}{c^2}}} \tag{10}
\end{align*}
\begin{align*}
f(v’_b)=\frac{1} {\sqrt{1 – \frac{\boldsymbol{u}’^2_b}{c^2}}} \tag{11}
\end{align*}
となります。
前述\( (7) \)(\(y\)方向の運動量保存則)が成立する\( f(u’_a) \)と\( f(u’_b) \)が\( (10) \)と\( (11) \)の通り決まりました。
どちらもローレンツ因子\(\gamma\)と\(v\)の関係と同じです。
したがって、物体の速度を\(u\)とすると\(\displaystyle \gamma=\frac{1} {\sqrt{1 – \frac{u^2}{c^2}}} \)を質量・速度に掛けることにより運動量保存則は成立します。実際、運動量はこのように定義されています。
まとめると、全ての慣性系において運動量は以下で表されます。
\begin{align*}
\boldsymbol{p} = \gamma m \boldsymbol{u}
\end{align*}
ただし、
\begin{align*}
\gamma=\frac{1} {\sqrt{1 – \frac{u^2}{c^2}}}
\end{align*}
です。
この定義における\(u\)は慣性系の相対速度ではなく、物体の速度である点に注意してください。また、\(\gamma\)も慣性系の相対速度から求められる値ではなく、物体の速度から求められる値です。
1.5 運動量の定義の確認1
前節まで、粒子の弾性衝突を例に特殊相対性理論で運動量保存則が成立するための運動量の定義を求めました。ただし、計算を簡単にするための特殊な例(衝突前後の粒子の速度が\(a\)と\(b\)で対称かつ粒子の質量が同じである場合)でした。
本節では一般的な場合(粒子の速度が対称、質量が同じとは限らない場合)についてもこの定義で運動量保存則が成立することを弾性衝突で確認します。
以下のように\(S\)における粒子の速度・質量を定義します。

同様に\(S’\)における速度・質量も定義します。\(S’\)は\(S\)から見て速度\((v, 0, 0)\)で移動しているものとします。
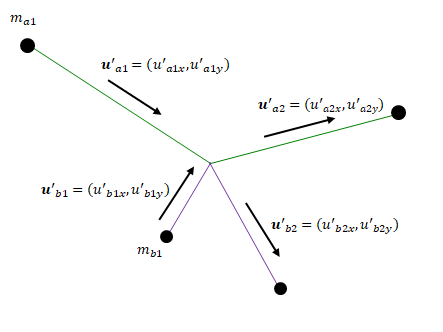
\(\gamma_{a1}\)なども以下のように定義します。
$$\gamma_{a1} = \frac {1} { \sqrt { 1 – \frac { u’^2_{a1} } {c^2} } } $$
\( \gamma_{b1} \)なども同様です。
\(S\)において、以下のように運動量保存則が成立しているものとします。
$$\gamma_{a1} m_{a} u_{a1x} + \gamma_{b1} m_{b} u_{b1x} = \gamma_{a2} m_{a} u_{a2x} + \gamma_{b2} m_{b} u_{b2x} \tag{12} $$
$$\gamma_{a1} m_{a} u_{a1y} + \gamma_{b1} m_{b} u_{b1y} = \gamma_{a2} m_{a} u_{a2y} + \gamma_{b2} m_{b} u_{b2y} \tag{13} $$
前節の結論通りであれば、\(S’\)においても以下のように運動量保存則が成立するはずです。
$$\gamma’_{a1} m_{a} u’_{a1x} + \gamma’_{b1} m_{b} u’_{b1x} = \gamma’_{a2} m_{a} u’_{a2x} + \gamma’_{b2} m_{b} u’_{b2x} \tag{14} $$
$$\gamma’_{a1} m_{a} u’_{a1y} + \gamma’_{b1} m_{b} u’_{b1y} = \gamma’_{a2} m_{a} u’_{a2y} + \gamma’_{b2} m_{b} u’_{b2y} \tag{15} $$
これを確認します。式が複雑なのでまずは衝突前の\(a\)のみに着目し、\(u’_{a1x}\)、\(u’_{a1y}\)が\(u_{a1x}\)、\(u_{a1y}\)、\(v\)、でどう表されるかを求めます。
速度の合成則により、
\begin{align}
u’_{a1x} = \frac { u_{a1x} – v } { 1 – \frac {u_{a1x} v} {c^2} }
\end{align}
\begin{align}
u’_{a1y} = \frac { \sqrt {1 – \frac {u^2} {c^2} } u_{a1y} } { 1 – \frac {u_{a1x} v} {c^2} }
\end{align}
両者の2乗和により、\(a\)の速さの2乗は、
\begin{align}
u_{1 a}^{\prime 2}&=\frac{\left(u_{a 1 x}-v\right)^{2}+\left(1-\frac{v^{2}}{c^{2}}\right) u_{a 1 y}^{2}}{\left(1-\frac{u_{a 1 x^{2}}}{c^{2}}\right)^{2}}\\
&=\frac{u_{a 1 x}^{2}-2 u_{a 1 x} v+v^{2}+u_{a 1 y}^{2}-\frac{u_{a 1 y}^{2}}{c^{2}}}{\left(1-\frac{u_{a 1 x}^{2}}{c^{2}}\right)^{2}}
\end{align}
これを用いて\(\gamma_{1a}\)は
\begin{align}
\gamma’_{a1}
&= \frac { 1 – \frac {u_{a1x} v} {c^2} }{\sqrt {\left (1 – \frac{v^2} {c^2} \right) \left ( 1 – \frac { u^2_{a1} } {c^2} \right)} } \\
\end{align}
となります。
過程を確認する場合は「+」を押して展開してください。
これに速度の各方向成分を掛けると、
\begin{align}
\gamma’_{a1} u’_{a1x} & = \frac {u_{a1x} – v}
{\sqrt {
\left (1 – \frac{v^2} {c^2} \right) \left ( 1 – \frac { u^2_{a1} } {c^2} \right)
} } \tag{16} \\
\end{align}
\begin{align}
\gamma’_{a1} v’_{a1y} & = \frac { \sqrt{1 – \frac {v^2} {c^2} } u_{a1y}}
{\sqrt {
\left (1 – \frac{v^2} {c^2} \right) \left ( 1 – \frac { u^2_{a1} } {c^2} \right)
} } \tag{17} \\
& = \frac { u_{a1y} }
{\sqrt { 1 – \frac { u^2_{a1} } {c^2} } }\\
\end{align}
\(b_1\)、\(a_2\)、\(b_2\)も同様です。
1.6 運動量の定義の確認2
前節で\(\gamma’_{a1} u’_{a1x}\)などが求められました。
これらを適用すれば\(S’\)における運動量保存則が成立するはずです。
まず\(x\)方向について確認します。
運動量保存則は以下の式でした。
$$\gamma’_{a1} m_{a} u’_{a1x} + \gamma’_{b1} m_{b} u’_{b1x} \stackrel{?}{=} \gamma’_{a2} m_{a} u’_{a2x} + \gamma’_{b2} m_{b} u’_{b2x} \tag{14} $$
系間の相対速度\(v\)を用いて、
$$ \gamma_{v} = \frac {1} {\sqrt { 1 – \frac {v^2} {c^2} } } $$
と定義します。さらに、既に定義された
$$ \gamma_{a1} = \frac {1} {\sqrt { 1 – \frac {u_{a1}^2} {c^2} } } $$
速度の合成則
$$u’_{a1x}=\frac {u_{a1x} – v} {1 – \frac {v^2} {c^2}}$$
などを用いて\( (14) \)は
$$ \gamma^2_{v} \gamma_{a1} m_{a} ( u_{a1x} – v) + \gamma^2_{v} \gamma_{b1} m_{b} ( u_{b1x} – v) \stackrel{?}{=} \gamma^2_{v} \gamma_{a2} m_{a} ( u_{a2x} – v) + \gamma^2_{v} \gamma_{b2} m_{b} ( u_{b2x} – v) $$
\(\gamma^2_v\)を消去し、
$$ \gamma_{a1} m_{a} ( u_{a1x} – v) + \gamma_{b1} m_{b} ( u_{b1x} – v) \stackrel{?}{=} \gamma_{a2} m_{a} ( u_{a2x} – v) + \gamma_{b2} m_{b} ( u_{b2x} – v) $$
となります。
これを二つの式に分解し、それぞれの等号が成立することを確認します。
$$ \gamma_{a1} m_{a} u_{a1x}+ \gamma_{b1} m_{b} u_{b1x} \stackrel{?}{=} \gamma_{a2} m_{b} u_{a2x} + \gamma_{b2} m_{b} u_{b2x} \tag{18}$$
$$ \gamma_{a1} m_{a} + \gamma_{b1} m_{b} \stackrel{?}{=} \gamma_{a2} m_{a} + \gamma_{b2} m_{b} \tag{19}$$
ただし、\( (19) \)は元の式の4つの項をそれぞれ\(-v\)で割っています。
さて、\( (18) \)は\( (14) \)そのものです。つまり、\(S\)における\(x\)方向の運動量保存則です。したがって、等号は成立します。
\( (19) \)に関しては\(E=\gamma mc^2\)を使います。特殊相対性理論においてもエネルギー保存則が成り立つはずです。であるとすれば、
$$\gamma_{a1} m_{a} c^2 + \gamma_{b1} m_{b} c^2 = \gamma_{a1} m_{a} c^2 + \gamma_{b2} m_{b} c^2$$
各項を\( c^2\)で割れば\( (19) \)になります。
以上、\( (18) \)と\( (19) \)の等号が成立することがわかったので、\( (14) \)は成立します。
エネルギー保存則が不要という点以外は\(y\)方向も同様なので\( (15) \)も成立します。
まとめると、\(S\)において以下
$$\gamma_{a1} m_{a} u_{a1x} + \gamma_{b1} m_{b} u_{b1x} = \gamma_{a2} m_{a} u_{a2x} + \gamma_{b2} m_{b} u_{b2x} \tag{12} $$
$$\gamma_{a1} m_{a} u_{a1y} + \gamma_{b1} m_{b} u_{b1y} = \gamma_{a2} m_{a} u_{a2y} + \gamma_{b2} m_{b} u_{b2y} \tag{13} $$
が成立するなら、\(S’\)においても以下
$$\gamma’_{a1} m_{a} u’_{a1x} + \gamma’_{b1} m_{b} u’_{b1x} = \gamma’_{a2} m_{a} u’_{a2x} + \gamma’_{b2} m_{b} u’_{b2x} \tag{14} $$
$$\gamma’_{a1} m_{a} u’_{a1y} + \gamma’_{b1} m_{b} u’_{b1y} = \gamma’_{a2} m_{a} u’_{a2y} + \gamma’_{b2} m_{b} u’_{b2y} \tag{15} $$
が成立します。
まとめると、
$$\boldsymbol{p} = \gamma m \boldsymbol{u}$$
という定義を使えば、
①どの慣性系でも
②衝突前の物体の速度・質量がどれだけであっても
運動量保存則が成立する、ということがいえます。
2 まとめ
・静止慣性系において速度\( (u_x, u_y, u_z) \)で運動する粒子の、相対速度\(v\)の移動系の座標では速度は以下のように表されます。
$$u’_x = \frac {u_x – v } {1 – \frac {u_x v} {c^2} } $$
$$u’_y = \frac{u_y }{\gamma \left(1-\frac{u_x v}{c^2}\right)}$$
$$u’_z = \frac{u_z }{\gamma \left(1-\frac{u_x v}{c^2}\right)}$$
ただし
$$\gamma =\frac{1} {\sqrt{1 – \frac{v^2}{c^2}}}$$
これを速度の合成則とよびます。
・特殊相対性理論における運動量は以下のように定義されます。
\begin{align*}
\boldsymbol{p} = \gamma m \boldsymbol{u}
\end{align*}
ただし、
\begin{align*}
\gamma=\frac{1} {\sqrt{1 – \frac{u^2}{c^2}}}
\end{align*}
・本ページでは、前項の運動量の定義にて、粒子の弾性衝突における運動量保存則が慣性系によらず成立することを確認しました。


