本ページでは、E=mc²の導出について考えてみましょう。意外にも、この式にたどり着くまでの過程は長くはありません。ただし、やや論理が飛躍していてすんなり理解できないかもしれません。ここではそのための補足もします。
1 \(E=mc^2\)
1.1 マクローリン展開
マクローリン展開とは、導関数(微分をした関数)を使って級数展開する方法の一つです。
展開する関数を\(f(x)\)とすると以下のように表すことができます。
$$f(x)=f^{(0)}(0) + f^{(1)}(0) x + \frac {f^{(2)}(0)} {2!} x^2 + \frac {f^{(3)}(0)} {3!} x^3 + \cdots \tag{1}$$
ただし、
$$\left . f^{(k)}(0) = \frac {d^k x} {dt^k} \right |_{x=0}$$
です。つまり、\(f^{(k)}(0)\)は\(k\)階の導関数(\(k\)回微分した関数)の\(x=0\)のときの値です。
これが正しいことを確認してみましょう。
$$f(x)=a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots \tag{2}$$
と表せるとします。
まず\( (2) \)に\(x=0\)を代入すると、
$$f^{(0)}(0) = a_0$$
となり、\(a_0\)が決定します。
次に\( (2) \)の両辺の1階導関数は、
$$f^{(1)}(x)=a_1 + 2 a_2 x + 3 a_3 x^2 + 4 a_4 x^3 +\cdots \tag{3}$$
\( (3) \)に\(x=0\)を代入すると、
$$f^{(1)}(0) = a_1$$
より、\(a_1\)が決定します。
\( (2) \)の両辺の2階導関数は、
$$f^{(2)}(x)= 2!a_2 + 3 \cdot 2 a_3 x + 4 \cdot 3 a_4 x^2 + 5 \cdot 4 a_5 x^3 + \cdots \tag{4}$$
\( (4) \)に\(x=0\)を代入すると、
$$f^{(2)}(0) = 2! a_2$$
より、\(a_2\)が決定します。
同様に、
$$f^{(3)}(0) = 3! a_3$$
$$f^{(4)}(0) = 4! a_4$$
$$\cdots$$
と決定します。これらの係数を\( (2) \)に代入すれば\( (1) \)と同じ式になります。つまり、この関係が成立することがわかります。
※\(x\)の値によっては発散することがあります。また、項の数が有限であった場合は無限の場合との差(剰余項)が発生します。ここではこれらについては考慮しません。
1.2 特殊相対性理論における運動エネルギー(1)
マクローリン展開を使って\(\displaystyle \gamma = \frac {1} {\sqrt{1 – \frac {u^2} {c^2}}} \)(物体の速度を\(u\)とします)を近似で表してみます。
\(\displaystyle \frac {1} {\sqrt{1 – x}} \)の1階導関数、2階導関数、3階導関数はそれぞれ
$$\frac {x} {2\left(1 – x \right)^{\frac{3}{2} } }$$
$$\frac {3} {4 \left (1- x \right)^{\frac{5}{2} } }$$
$$\frac {15} {8 \left (1- x \right)^{\frac{7}{2} } }$$
です。これをマクローリン展開の式に代入すると、
$$\frac {1} {\sqrt{1 – x}} = 1 + \frac {1} {2} x + \frac {3} {8} x^2 + \frac {5} {16} x^3 + \cdots$$
となります。
この式に\(\displaystyle \frac {u^2}{c^2}=x\)を代入し、さらに\(\displaystyle \gamma = \frac {1} {\sqrt{1 – \frac {u^2} {c^2}}} \)で置き換えると、
$$\gamma = 1 + \frac {1} {2} \frac {u^2} {c^2} + \frac {3} {8} \frac {u^4} {c^4} + \frac {5} {16} \frac {u^6} {c^6} + \cdots $$
\(u \ll c\)の場合、\(3\)項目以降は非常に小さく無視できできるので、
$$\gamma \approx 1 + \frac {1} {2} \frac {u^2} {c^2} $$
と近似できます。両辺より1を引いて\(mc^2\)を掛けると、
$$(\gamma -1) mc^2 \approx \left \{ \left( 1+ \frac {1} {2} \frac {u^2} {c^2} \right ) -1 \right \} mc^2 = \frac {1} {2} mu^2$$
です。
ニュートン力学における運動エネルギーと同じ式になりました。つまり\((\gamma -1) mc^2\)は\(u \ll c\)においてニュートン力学の運動エネルギーに漸近します。
したがって、これが特殊相対性理論における運動エネルギーであると考えることができます。特殊相対性理論における運動エネルギーを\(E_{kin}\)とすると、
$$E_{kin} = (\gamma – 1)mc^2$$
と定義されます。
\(kin\)は\(kinematic\)(物体の運動)の略です。
1.3 特殊相対性理論における運動エネルギー(2)
前節では\(u \ll c\)においてニュートン力学の運動エネルギーに近づくことから\( (\gamma – 1)mc^2\)が特殊相対性理論における運動エネルギーと定義される、と述べました。
別の方法で \( (\gamma – 1)mc^2 \)が特殊相対性理論における運動エネルギーであることを確認しましょう。
ニュートン力学では、運動エネルギーは、物体にはたらく力を変位で積分した値でした。
特殊相対性理論において同じ計算を行った場合、前節の運動エネルギーと定義と同じになるはずです。
粒子にはたらく力を\(\boldsymbol{F}\)、粒子の変位を\(d\boldsymbol{x}\)とします。ニュートン力学では運動エネルギーは
$$dE_{kin}=\boldsymbol{F} \cdot d\boldsymbol{x} \tag{1}$$
と表されます。特殊相対性理論でも同じように表されるものとします。
これを区間\( [0, x] \)の積分にすると
$$E_{kin}=\int_{0}^{x} \boldsymbol{F} \cdot d\boldsymbol{x}$$
となります。
前ページで求めたように\(\boldsymbol{p}=\gamma m \boldsymbol{u}\)として、
$$\boldsymbol{F} = \frac {d\boldsymbol{p} } {dt} = \frac {m d(\gamma \boldsymbol{u} )} {dt} $$
を\( (1) \)に代入すると、
$$E_{kin}=\int_{0} ^{x} \frac {m d(\gamma \boldsymbol{u} )} {dt} \cdot d\boldsymbol{x} $$
\( \displaystyle \frac {d\boldsymbol {x} } {dt} = \boldsymbol {u} \)を代入し、積分区間を\( [0, u] \)に変え、
$$E_{kin} = \int_{0}^{u} \boldsymbol{u} \cdot d (\gamma m\boldsymbol{u}) $$
この\( \gamma \)は物体とともに動く慣性系の相対速度と考えられるので、\( \displaystyle \gamma = \frac {1} {\sqrt {1 – \frac {u^2} {c^2} } } \)を代入し、
$$E_{kin} = \int_{0}^{u} \boldsymbol{u} \cdot d \Biggl\{ \frac {m\boldsymbol{u} } {\sqrt {1 – \frac {u^2} {c^2} } } \Biggr\} $$
部分和分の式
$$\int f dg = fg – \int g df $$
において、
$$f=\boldsymbol{u}$$
$$g=\frac {m\boldsymbol{u} } {\sqrt {1 – \frac {u^2} {c^2} } } $$
とすると、
$$E_{kin} = \frac {mu^2} {\sqrt{1 – \frac{u^2} {c^2} } } – \int_{0}^{u} m \frac {\boldsymbol{u}} {\sqrt{1 – \frac{u^2} {c^2} } } \cdot d\boldsymbol{u} $$
さらに計算を続けると
\begin{align}
E_{kin}
&= \frac {mu^2} {\sqrt{1 – \frac{u^2} {c^2} } } + \left [mc^2 \sqrt{1 – \frac{u^2} {c^2} } \right]_0^u \\
&= \frac {mu^2 + mc^2(1 – \frac{u^2} {c^2} ) } {\sqrt{1 – \frac{u^2} {c^2} } } – mc^2 \\
&= \frac {mc^2} {\sqrt{1 – \frac{u^2} {c^2} } } – mc^2\\
&=(\gamma – 1) mc^2
\end{align}
となります。ただし、\(u^2 = |\boldsymbol{u} |^2\)としています。
以上、物体の運動エネルギーを力の積分で求めると、前節と同じ結果になりました。
1.4 全体のエネルギーと静止エネルギー
1.2、1.3節より特殊相対性理論における物体の運動エネルギーが\(E_{kin} = (\gamma – 1)mc^2\)と定義されると述べました。
運動エネルギーは静止時には\(0\)になりますが、アインシュタインは静止時であっても\(mc^2\)だけのエネルギーが存在する、としました。このエネルギーを静止エネルギーとよびます。
物体が運動している場合も静止エネルギーは変わらず存在するため、静止エネルギーを\(E_{rest}\)とすると、物体全体のエネルギーは、
$$E_{total}=E_{kin}+E_{rest}= (\gamma – 1)mc^2+ mc^2 = \gamma mc^2$$
と表されます。
1.6-1.8節で静止エネルギーについて補足します。
その前に、\(E=mc^2\)とは静止エネルギーのことでしょうか。そのように定義される場合もありますが、一般的には全体のエネルギーのことを指します。次節でこのことについて述べます。
1.5 相対論的質量
ここまで、速度によって\(\gamma\)が変わるものとし、\(\gamma\)を用いてエネルギーを表しました。しかし\(\gamma\)を使わず、質量が速度によって変化するものとしてエネルギーを表すこともできます。
その場合、\(m_0\)を静止時の物体の質量、\(m\)を運動中の物体の質量とすると、
$$m=\gamma m_0 = \frac {m_0} {\sqrt {1- \frac {u^2} {c^2} } } $$
となります。つまり、速度が大きくなるほど質量は大きくなると考えられます。この\(m\)を相対論的質量とよびます。
\(m\)と\(m_0\)を用いて、
全体のエネルギーは
$$E_{total}=mc^2$$
静止エネルギーは
$$E_{rest}=m_0 c^2$$
と表されます。
結局、\(E=mc^2\)は静止エネルギーでしょうか、全体のエネルギーでしょうか。
前節の定義では静止エネルギーのことになりますが、一般的には全体のエネルギーとされます。つまり本節の定義です。どちらが正しいということではなく、表現の違いです。
なお、本サイトでは、断りがない限りは速度によって\(\gamma\)が変わる(質量は変わらない)ものとして表しています。
1.6 \(E_{total}\)と\(E_{rest}\)の解釈1:\(E_{kin}\)の導出過程より
1.4節では、\(E_{kin}=(\gamma-1)mc^2\)より\(E_{total} = \gamma mc^2\)と\(E_{rest}=mc^2\)が定義されると述べました。その解釈はいくつかありますが、本節より1.8節までその一部について述べます。
まず、1.3節の\(E_{kin}\)の計算を確認ください。
途中で区間\( [0, u] \)について定積分しました。その\(u\)における値が\(\gamma mc^2\)、\(0\)における値が\(mc^2\)でした。
つまり、静止しているときにも\(mc^2\)だけのエネルギーが存在し、運動しているときには運動エネルギーにこれが加算され、物体全体のエネルギーが\(\gamma mc^2\)となると考えることができます。
1.7 \(E_{total}とE_{rest}\)の解釈2:\(E_{kin}\)と\(\gamma\)の関係より
速度によって\(\gamma\)が変化するとし、速度の関数\(\gamma(u)\)によってエネルギーを表してみます。
全体のエネルギーを求めるときは速度を\(u\)として、
$$E_{total}=\gamma(u) mc^2$$
静止時は速度を\(0\)として、\(\gamma(0)=1\)より
$$E_{rest}=\gamma(0) mc^2$$
と表されます。つまり、\(E_{total}\)は速度\(u\)のときのエネルギー、\(E_{rest}\)は速度\(0\)のときのエネルギーと考えることができます。
1.8 \(E_{total}とE_{rest}\)の解釈3:\(E_{kin}\)と相対論的質量の関係より
次に、速度によって質量が変わるとした場合について考えてみます。
運動エネルギーは相対論的質量を用いて
$$E_{kin}=(m-m_0)c^2$$
と表されます。
下の図のように\(E_{kin}\)は\(m\)の増加に対して一定の割合(\(c^2\))で増加しますが、\(m=m_0\)のときに\(0\)になります。
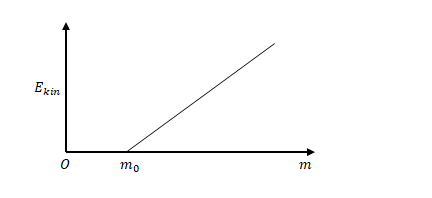
\(m\)が\(m_0\)より小さくなることがあると考えてみましょう。そのようなことは起こりえないと思えますが、1.9節の質量欠損がこれにあたります。とりあえず、\(m \lt m_0\)においても\(m\)の減少に対して\(E_{kin}\)は一定の割合で減少し、\(m=0\)において\(0\)となるエネルギー\(E\)を考えます。
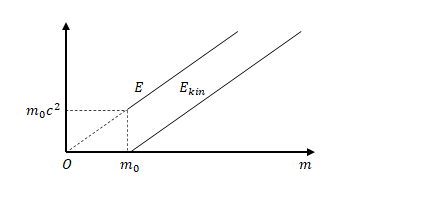
前述のように質量の変化に対するエネルギーの変化の割合を\(c^2\)とすると、\(m=m_0\)におけるエネルギーは
$$E_0=E_{kin}+m_0 c^2 = (m-m_0)c^2 + m_0 c^2 = m_0 c^2 $$
となります。この\(m_0 c^2\)が\(E_{rest}\)であると考えることができます。
1.9 光の放射エネルギーの例における\(E=\gamma mc^2\)の確認
次に、\(E_{kin}=(\gamma-1)mc^2\)より\(E_{total} = \gamma mc^2\)と\(E_{rest}=mc^2\)が定義されることの妥当性を、粒子から発する光のエネルギーの例から確認しましょう。
ある慣性系から見て静止している粒子が1つあります。この粒子から2方向に光を放射しており、どちら方向についても、その振動数(単位時間あたりの振動回数。工学で使われる「周波数」と同じ意味)は\(\nu\)、放射エネルギーは\(\displaystyle \Delta \frac {1} {2} E\)であるとします。
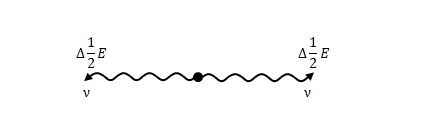
光のエネルギーは振動数と比例の関係があります。式にすると、
$$ \frac {1} {2} \Delta E \propto \nu $$
です。
次に、観測者から見てこの粒子が右方向に速度\(u\)で移動しているとします。
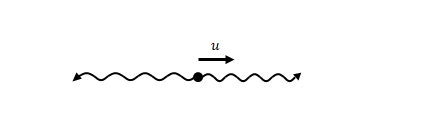
このエネルギーがどう変化するかを考えます。
粒子が速度\(u\)で移動する場合の振動数とエネルギーを下図のように定義します。

観測者から見て光源が移動する場合、ドップラー効果が生じます。光のドップラー効果は音のドップラー効果と似ていますが、光の場合はローレンツ変換に従うため、同じではありません。ここでは詳細を省略しますが、光のドップラー効果により以下のように周波数が変わります。
$$\nu’_0 = \frac {1 – \frac {u} {c} } {\sqrt {1 – \frac {u^2} {c^2} } } \nu $$
$$\nu’_1 = \frac {1 + \frac {u} {c} } {\sqrt {1 – \frac {u^2} {c^2} } } \nu $$
この周波数の変化により放射エネルギーも以下のように変わります。
$$\frac {1} {2} \Delta E’_0 = \frac {1 – \frac {u} {c} } {\sqrt {1 – \frac {u^2} {c^2} } } \frac {1} {2} \Delta E $$
$$\frac {1} {2} \Delta E’_1 = \frac {1 + \frac {u} {c} } {\sqrt {1 – \frac {u^2} {c^2} } } \frac {1} {2} \Delta E $$
両方向のエネルギーを足すと、
$$\Delta E’ = \frac {1 } {\sqrt {1 – \frac {u^2} {c^2} } } \Delta E $$
\(\gamma\)を用いて、
$$\Delta E’ = \gamma \Delta E $$
と表せます。
つまり、観測者から見て粒子が静止している状態から、速度\(u\)で移動している状態に変わると、放射エネルギーが\(\gamma\)倍になることを示しています。つまり、
$$E_{total} = \gamma E_{rest}$$
であるはずです。
一方、1.2-1.4節では、
$$E_{total}=E_{kin}+E_{rest}$$
$$E_{kin} = (\gamma – 1) m c^2$$
$$E_{total}=E_{kin}+E_{rest}$$
を導き、定義しました。
この3式を満たす条件は、
$$E_{total}=\gamma mc^2$$
$$E_{rest} = mc ^2$$
です。やはり1.4節の定義が妥当であることが確認できました。
1.10 \(E=mc^2\)にはどのような意味がある?
\(E=mc^2\)は物理的にどのような意味があるのでしょう。
\(m\)は質量、\(c\)は速さなので、\(mc^2\)は当然ですがエネルギーと同じ次元です。
\(c\)は定数です。もし光速が\(1\)となるような単位系でこれを表すと、\(E=m\)と、\(c\)を省略することができます。
つまり、\(E = mc^2\)は、質量とエネルギーは一定の量で交換が可能であるということを示しています。これを質量とエネルギーの等価性とよびます。
本当に交換可能なのでしょうか。少し例を挙げます。
核分裂という現象があります。原子力発電や核兵器で使われるプルトニウムなどは核分裂を起こします。その際、分裂後の物質の質量の総和は分裂前の質量より少なくなります。
これを質量欠損とよびます。質量欠損とは、何らかの反応前の質量の総和より、反応後の質量の総和が減ることです。これは原子が移動するというようなことではなく、完全にこの世から一部の質量が消えることです。
代わりにエネルギーが得られます。その関係が\(E=mc^2\)なのです。
質量の代わりに得られるエネルギーは膨大で、例えば日本が1年に消費するエネルギーはわずか20kgの質量から得られます。※
逆にエネルギーが増える場合もあります。物体にエネルギーを加えることによって質量は増えます。例えば、物質を高温・高圧にしていけばわずかですがその分質量は増えます。
※ 日本のエネルギー消費量は以下を参考にしました。
https://www.enerdata.net/estore/energy-market/japan/
1.11 \(E=mc^2\)は根拠があるといえる?
\(E_{total}\)、\(E_{rest}\)の導出についてどう感じたでしょうか。確固とした理論上の根拠があるといえるでしょうか。\(E_{kin} = (\gamma – 1)mc^2\)だから\(E_{total} = \gamma mc^2\)、\(E_{rest} = mc^2\)であるという結論は直観では正しそうですが、そう断言してよいのだろうか、と思いませんか。
また、\(E_{kin}=(\gamma – 1)mc^2\)も、低速においてニュートン力学における運動エネルギーに近似できるという理由しかありません。
本ページでは力を積分すると結果が一致することを確認しましたが、この力の定義も、遡ると運動量の定義を使っており、前ページの運動量の定義のために\(E_{total} = \gamma mc^2\)を使っているので論理が循環しています。
これらは何らかの根拠に基づいているのではなく、単なる定義でしかありません。しかし理論上破綻しているところはなく、実験による結果とも一致しています。したがってこれらの定義は妥当であるといえます。
2 まとめ
・\(\gamma\)をマクローリン展開すると、
$$\gamma = 1 + \frac {1} {2} \frac {u^2} {c^2} + \frac {3} {8} \frac {u^4} {c^4} + \frac {5} {16} \frac {u^6} {c^6} + \cdots $$
となることから、\(u \ll c\)においては
$$(\gamma -1) mc^2 \approx \frac {1} {2} mu^2$$
と、ニュートン力学における運動エネルギーに近づくことがわかります。このことより、特殊相対性理論における運動エネルギーは
$$E_{kin} = (\gamma -1) mc^2 $$
と定義されます。
・速度により\(\gamma\)が変化するとした場合、
物体全体のエネルギーは
$$E_{total}= \gamma mc^2 $$
静止エネルギーは
$$E_{rest}=mc^2 $$
と定義されます。
・速度により質量が変化するとした場合、
\(m_0\)を静止時の物体の質量、\(m\)を運動中の物体の質量とすると
$$m=\gamma m_0 = \frac {m_0} {\sqrt {1- \frac {u^2} {c^2} } } $$
と表され、
物体の全体のエネルギーは
$$E_{total} = mc^2$$
静止エネルギーは
$$E_{rest} = m_0 c^2$$
と定義されます。
