特殊相対性理論3(運動量)でも述べましたが、特殊相対性理論は「物理法則はどの慣性系においても同じ形式で表される」という原則(相対性原理)に基づき論じられています。しかし物理量の定義がニュートン力学のままではこの原則を守ることができません。
そこで一部の物理量は「固有時」を使って定義されています。本ページではこの固有時について述べます。
1 固有時
1.1 ローレンツ変換の変形
ローレンツ変換の式(以下)を一つの式にまとめてみましょう。
$$x’ = \gamma (x – vt) \tag{1}$$
$$t’ = \gamma \left( t – \frac {vx} {c^2} \right) \tag{2}$$
$$y’ = y \tag{3}$$
$$z’ = z \tag{4}$$
\( (1) \)、\( (3) \)、\( (4) \)の両辺を2乗、\( (2) \)の両辺に\(c\)を掛けて2乗します。
$$x’ ^2= \gamma^2 (x^2 – 2vxt + v^2t^2) \tag {4}$$
$$(ct’) ^2= \gamma^2 \left\{ (ct)^2 – 2vtx + \frac {v^2x^2} {c^2} \right\} \tag {5}$$
$$y’^2 = y^2 \tag {6}$$
$$z’^2 = z^2 \tag {7}$$
\( (5) – ( (4) + (6) + (7) ) \)を計算すると、
\begin{align}
\left(ct’\right)^2 – \left(x’^2 + y’^2+z’^2\right)
&= \gamma^2\left( c^2t^2 – \frac {v^2x^2} {c^2} – x^2 + v^2t^2\right) – y^2 – z^2 \\
&= \gamma^2\left( c^2t^2 – x^2 – v^2t^2 + \frac {v^2x^2} {c^2}\right) – y^2 – z^2 \\
&= \gamma^2\left\{ c^2t^2 – x^2 – \frac {v^2}{c^2} \left(c^2t^2 – x^2\right) \right\} – y^2 – z^2 \\
&= \gamma^2\left\{ \left( 1 – \frac {v^2}{c^2} \right) \left( c^2t^2 – x^2\right) \right\} – y^2 – z^2 \\
\end{align}
この式に
$$\gamma^2=\frac{1}{1-\frac{v^2}{c^2}}$$
を代入すると、
\begin{align}
\left(ct’\right)^2 – \left(x’^2 + y’^2+z’^2\right)= \left(ct \right)^2 – \left(x^2 + y^2 + z^2\right)
\end{align}
となります。一般的にはこれを\(s^2\)で表します(下式)。
$$s^2 = (ct’)^2 – (x’^2 + y’^2 + z’^2) = (ct)^2 – (x^2 + y^2 + z^2)\tag{8}$$
微小な増分として表すと、
$$ds^2 = (cdt’)^2 – (dx’^2 + dy’^2+dz’^2) = (cdt)^2 – (dx^2 + dy^2+dz^2)\tag{9}$$
となります。
1.2 ローレンツ不変
\( (9) \)にはどのような意味があるでしょう。
慣性系\(S\)を基準とすると、慣性系\(S’\)の座標である\(t’\)、\(x’\)、\(y’\)、\(z’\)は両者の相対速度によって変わる値です。にもかかわらず\( (9) \)は\(ds\)が相対速度に依存しない、つまり慣性系によって変わらないということを示しています。このような性質をローレンツ不変とよびます。
ローレンツ不変はどのような式でも成立するわけではありません。例えば、\( (ct)^2 + x^2 + y^2 + z^2 \)はローレンツ不変ではありません。
\(ds\)はローレンツ変換の式を変形して得られたものなのでローレンツ不変が成立することが確認できたのでした。その点で\( (9) \)は特別な意味をもっています。
1.3 固有時の定義
\(ds\)は慣性系によらず一定であることがわかりました。\(ds\)は時間と3次元の空間で表されますが、ある慣性系だけは\(ds\)は時間のみで表されます。どのような慣性系でしょう。
慣性系\(S\)から見て移動している粒子を考えます。
\(S’\)は粒子と同じ速度で移動しているとします。
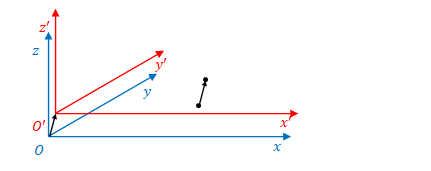
\(S’\)を基準にして見ると、粒子は静止しています。
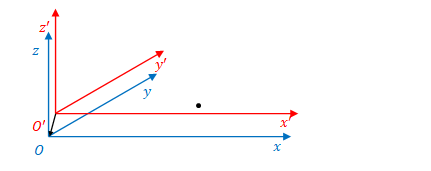
このとき\( (dx’, dy’, dz’) = (0,0,0) \)です。したがって、\( (9) \)は、
$$ds^2 = (cdt’)^2 = (cdt)^2 – (dx^2 + dy^2+dz^2)$$
となります。
つまり、物体と同じ速度で移動する慣性系では\(ds\)を時間だけで表しています。
この\(t’\)を\(\tau\)で表すことにします。\(\tau\)を使うと上の式は以下のように表されます。
$$(cd\tau)^2 = (cdt)^2 – (dx^2 + dy^2+dz^2)$$
\(ds\)はローレンツ不変なので、\(d\tau\)もローレンツ不変です。
この\(\tau\)を固有時(固有時間)とよびます。固有時は物体が静止して見える慣性系における時間の進み方を示しています。つまり、物体それぞれがもつ固有の時間と考えられるのでこの名があります。
1.4 \(d\tau\)は何に使われる?
冒頭で触れましたが、アインシュタインは物理法則はどの慣性系においても同じ形式で表すことができるはずであると述べています(相対性原理)。
しかし運動量はニュートン力学の定義のままでは運動量保存則が成り立たない場合があります。相対性原理にしたがうなら、以下のように運動量の定義を変える必要があるということがわかりました。
$$\boldsymbol {p} = \gamma m \boldsymbol {u}$$
しかし定義を変えないと相対性原理が守れなくなるのは運動量だけではありません。
そこで科学者は\(d\tau\)に注目したのでしょう。\(d\tau\)は\(dt\)と同じように時間のみの変数です。\(dt\)は慣性系によって値が変わるのに対し、\(d\tau\)は慣性系によって値が変わりません。そこで、\(dt\)の代わりに\(d\tau\)を使うことによって簡潔かつ慣性系によらない物理法則の記述ができるはずです。
物理量の定義については次ページで述べます。
1.5 \(dt\)と\(d\tau\)の関係
\(dt\)と\(d\tau\)の関係を求めてみましょう。
$$(cd\tau)^2=(cdt)^2-(x^2+y^2+z^2)$$
上の式の両辺を\(c\)で割り変形すると、
\begin{align}
(d\tau)^2&= dt^2 – \frac {dx^2+dy^2+dz^2} {c^2}\\
&= \left( 1 – \frac {dx^2+dy^2+dz^2 } {dt^2 c^2} \right) {dt^2}\\
&= \left( 1 – \frac {v^2 } {c^2} \right) {dt^2}\\
&= \gamma^2 {dt^2}\\
\end{align}
したがって、
$$dt = \gamma d\tau$$
となります。
非常に簡単な関係であることがわかりました。ではあえて\(d\tau\)を使う必要があるのでしょうか。次ページで述べますが、運動量に関しては\(\gamma\)を使うか\(\tau\)を使うかの違いしかないように思えます。しかし運動量以外の物理量の定義では\(dt\)を使うことにより複雑になるものがあります。\(\tau\)を使うとそのような複雑さはなく、慣性系によらない記述が可能です。
2 まとめ
・ローレンツ変換において、以下の関係は常に成立します。
$$(cdt’)^2 – (dx’^2 + dy’^2 + dz’^2) = (cdt)^2 – (dx^2 + dy^2 + dz^2)$$
つまり、\( (cdt)^2 – (dx^2 + dy^2 + dz^2)\)はローレンツ不変です。
・物体とともに移動する慣性系では\(dx’=dy’=dz’=0\)となるので前項の式は
$$(cdt’)^2= (cdt)^2 – (dx^2 + dy^2 + dz^2)$$
と表されます。
・このときの\(t’\)を一般的には\(\tau\)で表し、\(\tau\)を固有時とよびます。固有時もローレンツ不変です。
・特殊相対性理論では、それぞれの慣性系の時間を用いて物理量を定義すると、物理法則が慣性系によって異なる場合があります。これを避けるために固有時が使われます。
