特殊相対性理論17（電磁場の変換2）

前ページでは電荷をもった粒子周辺の電磁場を慣性系ごとに求めることにより電磁場の変換式を得ました。これとは別に、電磁場テンソルを使って導出することもできます。本ページでは電磁場テンソルを電磁ポテンシャル（マクスウェルの方程式6（電磁ポテンシャル））を使って定義することにより求める方法について述べます。

1 電磁場テンソルの定義

1.1 4元ベクトルの定義

電磁ポテンシャルは以下のように定義されるのでした（マクスウェルの方程式6（電磁ポテンシャル））。

$$\boldsymbol {B}=\nabla \times \boldsymbol{A} \tag{1} $$
$$\boldsymbol{E} = -\frac {\partial \boldsymbol{A}} {\partial t} -\nabla \Phi \tag{2}$$

\(\Phi\)はスカラー、\(\boldsymbol{A}\)は3次元ベクトルです。

そして、これらを合わせた4元ベクトルを

$$A^{\mu}=\left(\frac{\Phi}{c},\boldsymbol{A}\right) \tag{3}$$

と定義しました。

さらに、偏微分の演算子も以下のように4元ベクトルを定義します。

\begin{align}
\partial_{\nu} &= \left(\partial_0, \partial_1, \partial_2, \partial_3\right) \\
&= \left(\frac {\partial }{\partial x_0}, \frac {\partial }{\partial x_1}, \frac {\partial }{\partial x_2}, \frac {\partial }{\partial x_3} \right) \\
&= \left(\frac{1}{c}\frac {\partial }{\partial t}, \frac {\partial }{\partial x}, \frac {\partial }{\partial y}, \frac {\partial }{\partial z} \right) \tag{4}
\end{align}

\(0\)番目の成分だけ\(1/c\)がつくのは\(x^\mu=\left(ct, x,y,z\right)\)だからです。

1.2 電磁場と電磁ポテンシャルの関係

\( (2) \)を3次元ベクトルの成分ごとに表すと、

$$E_x= -\frac {\partial A_x} {\partial t} -\frac {\partial \Phi} {\partial x} \tag{5}$$

$$E_y= -\frac {\partial A_y} {\partial t} -\frac {\partial \Phi} {\partial y} \tag{6}$$

$$E_z= -\frac {\partial A_z} {\partial t} -\frac {\partial \Phi} {\partial z} \tag{7}$$

\( (3) \)と\( (4) \)の定義より、

$$E_x= – c \partial_0 A^1 – c \partial_1 A^0$$

$$E_y= – c \partial_0 A^2 – c \partial_2 A^0$$

$$E_z= – c \partial_0 A^3 – c \partial_3 A^0$$

両辺を\(c\)で割って、

$$\frac{E_x}{c} = – \partial_0 A^1 – \partial_1 A^0$$

$$\frac{E_y}{c} = – \partial_0 A^2 – \partial_2 A^0$$

$$\frac{E_z}{c} = – \partial_0 A^3 – \partial_3 A^0$$

と、電場を4元ベクトルで表すことができます。

\(A^{\nu}\)は反変ベクトルです（3.1節）。これを共変ベクトルに変えます。そのために\(1\)番目から\(3\)番目の成分（空間の成分）の符号を反転します（特殊相対性理論10（反変ベクトル・共変ベクトル2））。

$$\frac{E_x}{c} = \partial_0 A_1 – \partial_1 A_0 \tag{8}$$

$$\frac{E_y}{c} = \partial_0 A_2 – \partial_2 A_0 \tag{9}$$

$$\frac{E_z}{c} = \partial_0 A_3 – \partial_3 A_0 \tag{10}$$

次に\( (1) \)を成分ごとに分けます。

$$B_x = \partial_3 A^2 – \partial_2 A^3$$

$$B_y = \partial_1 A^3 – \partial_3 A^1$$

$$B_z = \partial_2 A^1 – \partial_1 A^2$$

回転（\(\nabla \times\)）の定義はベクトル場の回転を参照ください。

これも\(A^{\nu}\)を共変ベクトルに変えます。右辺の\(1\)番目と\(2\)番目の項を入れ替えています。

$$B_x = \partial_2 A_3 – \partial_3 A_2 \tag{11}$$

$$B_y = \partial_3 A_1 – \partial_1 A_3 \tag{12}$$

$$B_z = \partial_1 A_2 – \partial_2 A_1 \tag{13}$$

1.3 電磁場テンソルの定義

前節の\( (8)ｰ(13) \)はいずれも\(A_{\kappa}\)を\(x^{\lambda}\)で偏微分した項2つで表されます。そこで、

$$F_{\mu\nu}=\partial_{\mu} A_{\nu} – \partial_{\nu} A_{\mu} \tag{14}$$

で定義されるテンソルを考え、\( (8) -(13) \)をこの成分と対応させます。

   

\( (8)-(13) \)より、明らかに対角の成分は明らかに\(0\)で、対角線に関して対称な成分は符号が反転します（これを反対称テンソルとよびます）。テンソルを完成させると、

   

となります。このテンソルを電磁場テンソルとよびます。改めて前述の\(F_{\mu \nu}\)を用いると、

(15)  

と表されます。

これは2階共変テンソルです。2階反変テンソルに変えるには、\(1-3\)列目の符号を反転させ、さらに\(1-3\)行目の符号を反転させます。\(1-3\)列目かつ\(1-3\)行目の成分は\(2\)回反転して元に戻る点に注意してください。

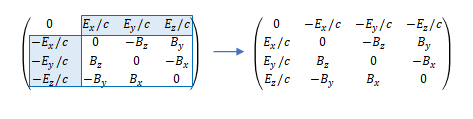
したがって2階反変の電磁場テンソルは

(16)  

と定義されます。

2 電磁場テンソルの変換

2.1 電磁場テンソルの変換

電磁場の変換式を得るために、座標系間における電磁場テンソルの関係を求めます。

慣性系\(S’\)においても、\( (14) \)と同じように電磁場テンソルは以下のように表されるはずです。

$$F’_{\mu \nu} = \partial’_{\mu} A’_{\nu} – \partial’_{\nu} A’_{\mu} \tag{17}$$

この式の右辺を\(F_{\mu \nu}\)に置き換えます。

\(A_{\nu}\)は共変ベクトルなので、

$$A’_{\nu} =\frac{\partial x_{\beta}}{\partial x^{\prime}_{\nu}}A_{\beta} \tag{18}$$

と表されます。これを\( (17) \)に代入して、

$$F’_{\mu \nu} = \frac{\partial}{\partial x’_\mu}\left(\frac{\partial x^{\beta}}{\partial x’_{\nu}}A_{\beta}\right) – \frac{\partial}{\partial x’_\nu}\left(\frac{\partial x^{\beta}}{\partial x’_{\mu}}A_{\beta}\right) \tag{19}$$

積の微分公式により、

\begin{align}
F’_{\mu \nu} &= \frac{\partial^2 x^\beta} {\partial x’_\mu \partial x’_\nu} A_\beta
+ \frac{\partial x^\alpha} {\partial x’_\mu} \frac{\partial x^\beta}{\partial x’_\nu} \partial_\alpha A_\beta
– \frac{\partial^2 x^\beta} {\partial x’_\nu \partial x’_\mu} A_\beta
– \frac{\partial x^\alpha} {\partial x’_\nu} \frac{\partial x^\beta}{\partial x’_\mu} \partial_\alpha A_\beta\\
&= \frac{\partial x^\alpha} {\partial x’_\mu} \frac{\partial x^\beta}{\partial x’_\nu} \partial_\alpha A_\beta
– \frac{\partial x^\alpha} {\partial x’_\nu} \frac{\partial x^\beta}{\partial x’_\mu} \partial_\alpha A_\beta\\
&= \frac{\partial x^\alpha} {\partial x’_\mu} \frac{\partial x^\beta}{\partial x’_\nu} \left(\partial_\alpha A_\beta – \partial_\beta A_\alpha \right)\\
&= \frac{\partial x^\alpha} {\partial x’_\mu} \frac{\partial x^\beta}{\partial x’_\nu} F_{\alpha \beta} \tag{20}
\end{align}

となります。

2.2 \(\Lambda\)を用いた電磁場テンソルの変換

\( (20) \)にて\(F’_{\mu \nu}\)と\(F_{\alpha \beta}\)の関係が得られました。この式の中の偏微分を定数に変えます。

2階共変テンソルではなく、共変ベクトルの変換について考えてみましょう。これを\(f_\mu\)とすると、\(S’\)では、

$$f’_\mu = \frac{\partial x_\mu} {\partial x’_\alpha} f_\mu \tag{21}$$

と表されます。

また、ローレンツ変換の係数\(\Lambda\)を使って

$$f’_\mu = \left(\Lambda^{-1}\right)^\mu _{\ \ \ \alpha}f_\mu \tag{22}$$

と表すこともできます。

これは共変ベクトルの場合でしたが、反変ベクトルの場合は変換の方向が反転し、

$$f^{\prime\mu} = \Lambda^\mu _{\ \ \ \alpha}f^\mu \tag{23}$$

となります。

同様に電磁場テンソルを2階共変テンソルから2階反変テンソルに変え、\(\Lambda\)を用いて、

$$F^{\prime \mu \nu} = \Lambda ^\mu_{\ \ \ \alpha} \Lambda ^\nu_{\ \ \ \beta} F^{\mu \nu} \tag{24}$$

となります。

2.3 演算順序の変更

\( (25) \)の\(F^{\prime \mu \nu}\)と\(F^{\mu \nu}\)に電磁場を代入すれば電磁場の変換式を得られるのですが、そのままでは計算が簡単ではないので演算の順序を入れ替えます。

この式には添え字が4種類存在します。そこでまず\(\mu\)、\(\nu\)、\(\beta\)が\(0\)で\(\alpha\)が\(0\)から\(3\)まで変化した場合を考えます。下の図がそのイメージです。

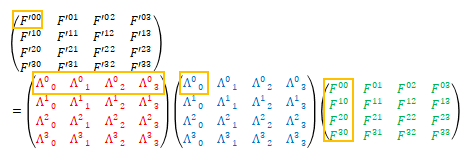
次に\(\mu\)、\(nu\)、\(\alpha\)が\(0\)で\(\beta\)が\(0\)から\(3\)まで変化する場合です。

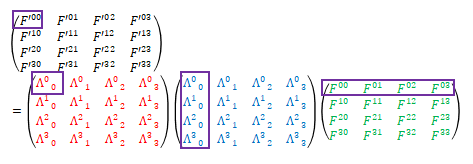
ここで、\(\Lambda ^\nu_{\ \ \ \beta}\)と\( F^{\mu \nu}\)を入れ替えます。その際、\(\Lambda ^\nu_{\ \ \ \beta}\)を転置（対角について対称な位置と成分を交換）します。

改めて、\(\mu\)、\(\nu\)、\(\beta\)が\(0\)で\(\alpha\)が\(0\)から\(3\)に変化する場合は

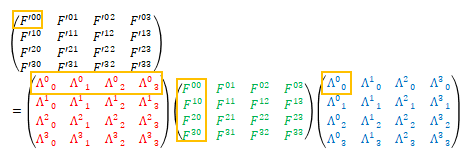
\(\mu\)、\(\nu\)、\(\alpha\)が\(0\)で\(\beta\)が\(0\)から\(3\)の場合は

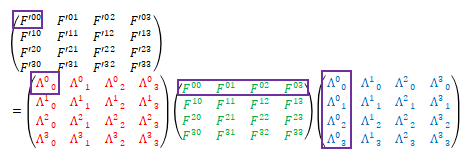
となります。行列の積と同じ演算になるので添え字を一部省略して、

$$F^{\prime \mu \nu} = \left( \Lambda F^{\mu \nu} \Lambda ^T \right)^{\mu \nu} \tag{26}$$

と表すことにします。添え字の\(T\)は転置を表します。

2.4 電磁場の代入

\( (26) \)を計算します。

   

ここで、

$$\gamma^2 – \beta^2\gamma^2=\gamma^2\left(1-\beta^2\right)=\frac{1}{1-\beta^2}\left(1-\beta^2\right)=1$$

であることを利用し、

   

右辺を

$$\beta=\frac{v}{c}$$

で置き換え、

   

これを変換後の電磁場テンソルの定義

   

と比較し、

$$E’_x=E_x \tag{27}$$

$$E’_y=\gamma\left(E_y-vB_z\right) \tag{28}$$

$$E’_z=\gamma\left(E_z+vB_y\right) \tag{29}$$

$$B’_x=B_x \tag{30}$$

$$B’_y=\gamma\left(B_y+\frac{v}{c^2}E_z\right) \tag{31}$$

$$B’_z=\gamma\left(B_z-\frac{v}{c^2}E_y\right) \tag{32}$$

となります。以上、電磁場の変換の式が得られました。

3 補足

3.1 \(A^{\mu}\)は反変ベクトル？

本ページでは\(A^{\mu}\)を反変ベクトルであるとして電磁場の変換式を求めました。

ここで、\(A^{\mu}\)は本当に反変ベクトルであることを確認しましょう。

まず、この4元速度と4元電流密度の関係についてです。電荷が移動しているところを考えます。その速度を3次元ベクトルで\(\boldsymbol{u}\)、電流密度を\(\boldsymbol{J}\)とすると、

$$\boldsymbol{J}=\rho \boldsymbol{u} \tag{33}$$

の関係があります（次節参照）。

4元速度は、

$$u^{\nu}=\left(c,\boldsymbol{u}\right) \tag{34}$$

と定義しました（特殊相対性理論6（4元ベクトル））。

\( (33) \)と\( (34) \)より4元電流密度は、

$$J^{\nu}=\rho u^{\nu} = \left(c\rho,\boldsymbol{J} \right) \tag{35}$$

と定義できます。

次に、4元電流密度と4元電磁ポテンシャルの関係についてです。両者は以下の関係にありました（マクスウェルの方程式6（電磁ポテンシャル））。

$$ □ A^{\nu} = -\mu_0 J^{\nu} \tag{36}$$

\(□\)はダランベール演算子（ダランベルシアン）で、

$$ \nabla^2 – \frac{1}{c^2} \frac {\partial^2} {\partial t^2} \tag{37}$$

の意味です。

さて、\(x^{\nu}\)は以下のように表すことができるので反変ベクトルです。

$$x^{\prime\mu}=\frac {d x^{\prime \mu}} {d x^{\nu}} x^{\nu} \tag{38}$$

これを時間について微分した4元速度も反変ベクトルです。

$$u^{\prime\mu}=\frac {d x^{\prime \mu}} {d x^{\nu}} u^{\nu} \tag{39}$$

\(u^{\nu}\)が反変ベクトルであれば、\( (35) \)より、明らかに\(J^{\nu}\)も反変ベクトルです。さらに\( (36) \)より明らかに\(A^{\nu}\)も反変ベクトルです。

また、\(A^{\nu}\)が反変ベクトルであれば、

$$A_{\mu}=\left(\frac{\Phi}{c},-\boldsymbol{A}\right) \tag{40}$$

は共変ベクトルです。

3.2 電荷密度と電流密度の関係

前節の\( (33) \)、つまり電荷密度と速度の積は電流密度であることを確認しましょう。

ある面における電流とは、単位時間の間にその面を通る電荷の量です。

下の図のように直方体の領域において電荷が移動しているところを考えます。\(\Delta t\)の間に電荷が\(\Delta x\)だけ移動しており、移動方向に垂直な2辺が\(y\)、\(z\)であるとします。また、電荷の速度を\(u_x\)とし電流密度と速度の関係を求めます。

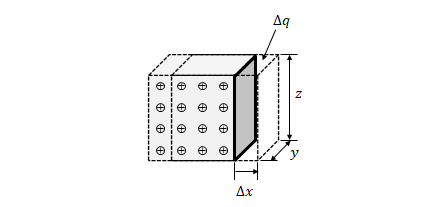
\(\Delta t\)の間に移動した電荷を\(\Delta q\)、電荷密度\(\rho\)とすると、

$$\Delta q=\rho \Delta x y z = \rho {u_x}{\Delta t} y z \tag{41}$$

電流は、

$$I = \frac{\Delta q}{\Delta t} = \rho u_x y z \tag{42}$$

電流密度は、

$$J = \frac{I}{y z} = \rho u_x \tag{43}$$

ここまではスカラーとして計算しましたが、明らかにどの方向についても同様に成立するのでベクトルを用いて

$$\boldsymbol{J}=\rho \boldsymbol{u} \tag{44}$$

と表すことができます。

4 まとめ

・電磁ポテンシャルの定義は以下でした。
$$\boldsymbol {B}=\nabla \times \boldsymbol{A} $$
$$\boldsymbol{E} = -\frac {\partial \boldsymbol{A}} {\partial t} -\nabla \Phi $$

・電磁場テンソルを定義します（共変ベクトルの場合）。
$$F_{\mu\nu}=\partial_{\mu} A_{\nu} – \partial_{\nu} A_{\mu} $$

・電磁場テンソルを電磁場で表すと（反変ベクトルの場合）、

   

・座標変換した電磁場テンソルを計算すると、

   

・座標変換した電磁場テンソルを、定義に基づいて表すと、

   

・両者を比較して以下が得られます。

$$E’_x=E_x $$

$$E’_y=\gamma\left(E_y-vB_z\right) $$

$$E’_z=\gamma\left(E_z+vB_y\right) $$

$$B’_x=B_x $$

$$B’_y=\gamma\left(B_y+\frac{v}{c^2}E_z\right) $$

$$B’_z=\gamma\left(B_z-\frac{v}{c^2}E_y\right) $$