特殊相対性理論10（反変ベクトル・共変ベクトル2）

特殊相対性理論7（反変ベクトル・共変ベクトル1）で、反変・共変については深く触れないと述べたところですが、もう少し話したいことがあります。教科書には「$ (x^0, x^1, x^2, x^3) $を反変ベクトルとする」「$ (x_0, -x_1, -x_2, -x_3) $を共変ベクトルとする」と書かれていることがありますが、その理由について説明されることは少ないと思います。

本ページではなぜそのように定義されるかを、反変・共変ベクトルの定義とローレンツ変換の関係から考えます。

1 反変ベクトル・共変ベクトルの定義

1.1 偏微分による反変ベクトルの定義

「特殊相対性理論7（反変ベクトル・共変ベクトル1）」のページで反変ベクトルの定義について述べましたが、アインシュタインの縮約記法を使って表すと以下のようになります。

$$a’^{\mu} = \frac {\partial x’^{\mu}} {\partial x ^{\nu}} a^{\nu} \tag{1}$$

右辺の$\nu$は擬標である点に注意してください。この式は以下と同じ意味です。

$$a’^0 = \frac {\partial x’^0} {\partial x ^0} a^0 + \frac {\partial x’^0} {\partial x ^1} a^1 + \frac {\partial x’^0} {\partial x ^2} a^2 + \frac {\partial x’^0} {\partial x ^3} a^3$$

$$a’^1 = \frac {\partial x’^1} {\partial x ^0} a^0 + \frac {\partial x’^1} {\partial x ^1} a^1 + \frac {\partial x’^1} {\partial x ^2} a^2 + \frac {\partial x’^1} {\partial x ^3} a^3$$

$$a’^2 = \frac {\partial x’^2} {\partial x ^0} a^0 + \frac {\partial x’^2} {\partial x ^1} a^1 + \frac {\partial x’^2} {\partial x ^2} a^2 + \frac {\partial x’^2} {\partial x ^3} a^3$$

$$a’^3 = \frac {\partial x’^3} {\partial x ^0} a^0 + \frac {\partial x’^3} {\partial x ^1} a^1 + \frac {\partial x’^3} {\partial x ^2} a^2 + \frac {\partial x’^3} {\partial x ^3} a^3$$

1.2 偏微分による共変ベクトルの定義

共変ベクトルの定義はアインシュタインの縮約記法を使うと以下のようになります。

$$a’_{\mu} = \frac {\partial x^{\nu}} {\partial x’ ^{\mu}} a_{\nu} \tag{2}$$

アインシュタインの縮約記法を使わない場合は以下です。

$$a’_0 = \frac {\partial x^0} {\partial x’^0} a_0 + \frac {\partial x^0} {\partial x’ ^1} a_1 + \frac {\partial x^0} {\partial x’^2} a_2 + \frac {\partial x^0} {\partial x’^3} a_3$$

$$a’_1 = \frac {\partial x^1} {\partial x’^0} a_0 + \frac {\partial x^1} {\partial x’ ^1} a_1 + \frac {\partial x^1} {\partial x’^2} a_2 + \frac {\partial x^1} {\partial x’^3} a_3$$

$$a’_2 = \frac {\partial x^2} {\partial x’^0} a_0 + \frac {\partial x^2} {\partial x’ ^1} a_1 + \frac {\partial x^2} {\partial x’^2} a_2 + \frac {\partial x^2} {\partial x’^3} a_3$$

$$a’_3 = \frac {\partial x^3} {\partial x’^0} a_0 + \frac {\partial x^3} {\partial x’ ^1} a_1 + \frac {\partial x^3} {\partial x’^2} a_2 + \frac {\partial x^3} {\partial x’^3} a_3$$

1.3 座標変換の係数による反変ベクトルの定義

1.1節の反変ベクトルの定義は偏微分を使っていますが、偏微分を使わず、座標変換の式で現れる係数で表すことができます

以下のように1次元の座標変換について考えます。

$$x’=kx$$

$x’$を縦軸、$x$を横軸のグラフを考えると$k$は傾きなので微分を用いると

$$k^{-1}=\frac {d x} {d x’} $$

となります。したがって$x$と$x’$の関係は

$$x=\frac {d x} {d x’} x’$$

と表すこともできます。

この関係を4次元に拡張してみましょう。

座標変換が以下のように定義されているとします。

$$x’^{\mu} = k^{\mu}_{\ \ \nu} x^{\nu} \tag{3}$$

行列とベクトルで表すと以下です。

$\begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix} =\begin{pmatrix} k^{0}_{\ \ 0} & k^{0}_{\ \ 1} & k^{0}_{\ \ 2} & k^{0}_{\ \ 3} \\ k^{1}_{\ \ 0} & k^{1}_{\ \ 1} & k^{1}_{\ \ 2} & k^{1}_{\ \ 3} \\ k^{2}_{\ \ 0} & k^{2}_{\ \ 1} & k^{2}_{\ \ 2} & k^{2}_{\ \ 3} \\ k^{3}_{\ \ 0} & k^{3}_{\ \ 1} & k^{3}_{\ \ 2} & k^{3}_{\ \ 3} \end{pmatrix} \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} \\$

偏微分を使って書き直すと、

$$x’^{\mu} = \frac {\partial x’^{\mu}} {\partial x ^{\nu}} x^{\nu} \tag{4}$$

$\begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix} =\begin{pmatrix} \frac {\partial x'^0} {\partial x^0} & \frac {\partial x'^0} {\partial x^1} & \frac {\partial x'^0} {\partial x^2} & \frac {\partial x'^0} {\partial x^3} \vspace{3pt} \\ \frac {\partial x'^1} {\partial x^0} & \frac {\partial x'^1} {\partial x^1} & \frac {\partial x'^1} {\partial x^2} & \frac {\partial x'^1} {\partial x^3} \vspace{3pt} \\ \frac {\partial x'^2} {\partial x ^0} & \frac {\partial x'^2} {\partial x^1} & \frac {\partial x'^2} {\partial x^2} & \frac {\partial x'^2} {\partial x^3} \vspace{3pt} \\ \frac {\partial x'^3} {\partial x ^0} & \frac {\partial x'^3} {\partial x ^1} & \frac {\partial x'^3} {\partial x^2} & \frac {\partial x'^3} {\partial x^3} \end{pmatrix} \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} \\$

となります。

$ (3) $と$ (4) $は等価なので、右辺の係数を比較すると、

$$k^{\mu} = \frac {\partial x’^{\mu}} {\partial x ^{\nu}} x^{\nu} \tag{5}$$

の関係にあります。

次に、反変ベクトルの定義について考えます。

$$a’^{\mu} = \frac {\partial x’^{\mu}} {\partial x ^{\nu}} a^{\nu} \tag{1}$$

$\begin{pmatrix} a'^0 \\ a'^1 \\ a'^2 \\ a'^3 \end{pmatrix} =\begin{pmatrix} \frac {\partial x'^0} {\partial x^0} & \frac {\partial x'^0} {\partial x^1} & \frac {\partial x'^0} {\partial x^2} & \frac {\partial x'^0} {\partial x^3} \vspace{3pt} \\ \frac {\partial x'^1} {\partial x^0} & \frac {\partial x'^1} {\partial x^1} &\frac {\partial x'^1} {\partial x^2} & \frac {\partial x'^1} {\partial x^3} \vspace{3pt} \\ \frac {\partial x'^2} {\partial x^0} & \frac {\partial x'^2} {\partial x^1} & \frac {\partial x'^2} {\partial x^2} & \frac {\partial x'^2} {\partial x^3} \vspace{3pt} \\ \frac {\partial x'^3} {\partial x^0} & \frac {\partial x'^3} {\partial x^1} & \frac {\partial x'^3} {\partial x^2} & \frac {\partial x'^3} {\partial x^3} \end{pmatrix} \begin{pmatrix} a^0 \\ a^1 \\ a^2 \\ a^3 \end{pmatrix} \\$

$ (4) $と$ (1) $の右辺の係数を比較してください。

同じですね。

したがって$ (5) $の関係を適用し、

$$a’^{\mu} = k^{\mu}_{\ \ \nu} a^{\nu} \tag{6}$$

$\begin{pmatrix} a'^0 \\ a'^1 \\ a'^2 \\ a'^3 \end{pmatrix} =\begin{pmatrix} k^{0}_{\ \ 0} & k^{0}_{\ \ 1} & k^{0}_{\ \ 2} & k^{0}_{\ \ 3} \\ k^{1}_{\ \ 0} & k^{1}_{\ \ 1} & k^{1}_{\ \ 2} & k^{1}_{\ \ 3} \\ k^{2}_{\ \ 0} & k^{2}_{\ \ 1} & k^{2}_{\ \ 2} & k^{2}_{\ \ 3} \\ k^{3}_{\ \ 0} & k^{3}_{\ \ 1} & k^{3}_{\ \ 2} & k^{3}_{\ \ 3} \end{pmatrix} \begin{pmatrix} a^0 \\ a^1 \\ a^2 \\ a^3 \end{pmatrix} \\$

と表すことができます。

整理しましょう。

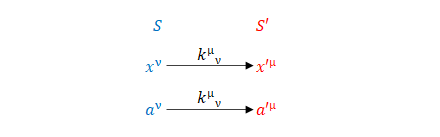
座標変換が

$$x’^{\mu} = k^{\mu}_{\ \ \nu} x^{\nu}$$

と定義されているとします。

ベクトル$a^{\mu}$の変換が同じ係数で表されるとき、つまり

$$a’^{\mu} = k^{\mu}_{\ \ \nu} a^{\nu} \tag{7}$$

の関係のとき、$a^{\mu}$は反変ベクトルです。

1.3 共変ベクトルの別定義

同様に共変ベクトルの条件も座標変換との関連で定義できます。

ただし反変ベクトルとは異なり、逆変換との一致が条件です。

1次元の座標を考えます。

$$x’=kx$$

関係を逆にします。

$$x=k^{-1}x’$$

$x$を縦軸、$x’$を横軸のグラフを考えると$k^{-1}$は傾きなので微分を用いて

$$k^{-1}=\frac {d x} {d x’} $$

となります。したがって$x$と$x’$の関係は

$$x=\frac {d x} {d x’} x’$$

と表すこともできます。

この関係を4次元に拡張します。

以下の座標変換を

$$x’^{\mu} = k^{\mu}_{\ \ \nu} x^{\nu} \tag{3}$$

逆にすると以下のように表されるとします。

$$x^{\mu} = \left( k^{-1} \right) ^{\mu}_{\ \ \nu} x’^{\nu} = m^{\mu}_{\ \ \nu} x’^{\nu} \tag{8}$$

$\begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix} =\begin{pmatrix} m^{0}_{\ \ 0} & m^{0}_{\ \ 1} & m^{0}_{\ \ 2} & m^{0}_{\ \ 3} \\ m^{1}_{\ \ 0} & m^{1}_{\ \ 1} & m^{1}_{\ \ 2} & m^{1}_{\ \ 3} \\ m^{2}_{\ \ 0} & m^{2}_{\ \ 1} & m^{2}_{\ \ 2} & m^{2}_{\ \ 3} \\ m^{3}_{\ \ 0} & m^{3}_{\ \ 1} & m^{3}_{\ \ 2} & m^{3}_{\ \ 3} \end{pmatrix} \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} \\$

偏微分を使って書き直すと、

$$x^{\mu} = \frac {\partial x^{\nu}} {\partial x’ ^{\mu}} x’^{\nu} \tag{9}$$

$\begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} =\begin{pmatrix} \frac {\partial x^0} {\partial x'^0} & \frac {\partial x^0} {\partial x'^1} & \frac {\partial x^0} {\partial x'^2} & \frac {\partial x^0} {\partial x'^3} \vspace{3pt} \\ \frac {\partial x^1} {\partial x'^0} & \frac {\partial a^1} {\partial x'^1} & \frac {\partial x^1} {\partial x'^2} & \frac {\partial x^1} {\partial x'^3} \vspace{3pt} \\ \frac {\partial x^2} {\partial x'^0} & \frac {\partial x^2} {\partial x'^1} & \frac {\partial x^2} {\partial x'^2} & \frac {\partial x^2} {\partial x'^3} \vspace{3pt} \\ \frac {\partial x^3} {\partial x'^0} & \frac {\partial x^3} {\partial x'^1} & \frac {\partial x^3} {\partial x'^2} & \frac {\partial x^3} {\partial x'^3} \end{pmatrix} \begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix} \\$

となります。

$ (8) $と$ (9) $は等価なので、

$$ \left( k^{-1} \right) ^{\mu}_{\ \ \nu} = \frac {\partial x^{\nu}} {\partial x’ ^{\mu}} \tag{10}$$

です。

次に、共変ベクトルの定義について考えます。

$$a’_{\mu} = \frac {\partial x^{\nu}} {\partial x’ ^{\mu}} a_{\nu} \tag{2}$$

$\begin{pmatrix} a'_0 \\ a'_1 \\ a'_2 \\ a'_3 \end{pmatrix} =\begin{pmatrix} \frac {\partial x^0} {\partial x'^0} & \frac {\partial x^0} {\partial x^1} & \frac {\partial x^0} {\partial x'^2} & \frac {\partial x'^0} {\partial x^3} \vspace{3pt} \\ \frac {\partial x^1} {\partial x'^0} & \frac {\partial x^1} {\partial x'^1} & \frac {\partial ^1} {\partial x'^2} & \frac {\partial x^1} {\partial x'^3} \vspace{3pt} \\ \frac {\partial x^2} {\partial x'^0} & \frac {\partial x^2} {\partial x'^1} & \frac {\partial x^2} {\partial x'^2} & \frac {\partial x^2} {\partial x'^3} \vspace{3pt} \\ \frac {\partial x^3} {\partial x'^0} & \frac {\partial x^3} {\partial x'^1} & \frac {\partial x^3} {\partial x'^2} & \frac {\partial x^3} {\partial x'^3} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \end{pmatrix} \\$

$ (8) $と$ (2) $の右辺の係数は一致します。

したがって$ (10) $の関係を適用し、

$$a’^{\mu} = \left( k^{-1} \right) ^{\mu}_{\ \ \nu} a^{\nu} \tag{11}$$

$\begin{pmatrix} a'^0 \\ a'^1 \\ a'^2 \\ a'^3 \end{pmatrix} =\begin{pmatrix} m^{0}_{\ \ 0} & m^{0}_{\ \ 1} & m^{0}_{\ \ 2} & m^{0}_{\ \ 3} \\ m^{1}_{\ \ 0} & m^{1}_{\ \ 1} & m^{1}_{\ \ 2} & m^{1}_{\ \ 3} \\ m^{2}_{\ \ 0} & m^{2}_{\ \ 1} & m^{2}_{\ \ 2} & m^{2}_{\ \ 3} \\ m^{3}_{\ \ 0} & m^{3}_{\ \ 1} & m^{3}_{\ \ 2} & m^{3}_{\ \ 3} \end{pmatrix} \begin{pmatrix} a^0 \\ a^1 \\ a^2 \\ a^3 \end{pmatrix} \\$

と表すことができます。

整理します。

座標変換が

$$x’^{\mu} = k^{\mu}_{\ \ \nu} x^{\nu} $$

と定義されているとします。

ベクトル$a_{\nu}$の変換が座標の逆変換の係数で表されるとき、つまり

$$a’_{\mu} = \left( k^{-1} \right) _{\mu}^{\ \ \nu} a_{\nu}\tag{12}$$

の関係のとき、$a_{\nu}$は共変ベクトルです。

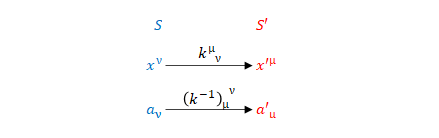
2 $ (x^0, x^1, x^2, x^3) $ $/ $ $ (x_0, -x_1, -x_2, -x_3) $は反変/共変ベクトル？

前章では座標変換の条件を限定しませんでしたが、本章における座標変換とはローレンツ変換のことを指しますので注意ください。

2.1 $ (x^0, x^1, x^2, x^3) $は反変ベクトル？

$ (x^0, x^1, x^2, x^3) $が反変ベクトルであることを確かめます。

以下がローレンツ変換の式です。

$$x’ ^ {\mu} = \Lambda ^{\mu} _ {\ \ \nu} x^{\nu} \tag{13}$$

反変ベクトルの条件は、$ (6) $の$k$を$\Lambda$に変えて

$$a’^{\mu} = \Lambda ^{\mu}_{\ \ \nu} a^{\nu} \tag{14}$$

です。

今、$a^{\nu}=(x^0, x^1, x^2, x^3) $ が反変ベクトルであることを確認しようとしています。

ということは$ (13) $、$ (14) $どちらも以下の式になります。

(15) $\begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix} =\begin{pmatrix} \gamma & -\beta \gamma & 0 & 0\\ -\beta \gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix}$

したがって$(x^0, x^1, x^2, x^3) $ は反変ベクトルです。

2.2 $ (x_0, -x_1, -x_2, -x_3) $は共変ベクトル？

$ (x_0, -x_1, -x_2, -x_3) $が共変ベクトルであることを確かめます。

以下がローレンツ逆変換です。

$$x ^ {\mu} = (\Lambda^{-1}) ^{\mu} _{\ \ \nu} x’^{\nu} \tag{16}$$

共変ベクトルの条件は、$ (12) $の$k^{-1}$を$\Lambda^{-1}$に変え、

$$a’_{\mu} = \left( \Lambda^{-1} \right) _{\mu}^{\ \ \nu} a_{\nu}\tag{17}$$

です。

これは$ (17) $が

$$a_{\nu} = (x_0, -x_1, -x_2, -x_3)$$

において成立する、つまり

(18) $\begin{pmatrix} x'_0 \\ -x'_1 \\ -x'_2 \\ -x'_3 \end{pmatrix} \stackrel{?}{=}\begin{pmatrix} \gamma & \beta \gamma & 0 & 0\\ \beta \gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_0 \\ -x_1 \\ -x_2 \\ -x_3 \end{pmatrix}$

であることがいえるのであれば共変ベクトルです。

そこで、この両辺に$\eta^{\mu \nu}$を掛けます。

$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x'_0 \\ -x'_1 \\ -x'_2 \\ -x'_3 \end{pmatrix}\vspace{3pt}\\ \stackrel{?}{=} \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} \gamma & \beta \gamma & 0 & 0\\ \beta \gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_0 \\ -x_1 \\ -x_2 \\ -x_3 \end{pmatrix}$

左辺の1-3行目の符号が反転します。

$\begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix} \stackrel{?}{=} \begin{pmatrix} \gamma & -\beta \gamma & 0 & 0\\ \beta \gamma & -\gamma & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x^0 \\ -x^1 \\ -x^2 \\ -x^3 \end{pmatrix}$

さらに両辺に$ \left( \Lambda^{-1} \right) _{\mu}^{\ \ \nu} $を掛けます。

$\begin{pmatrix} \gamma & \beta \gamma & 0 & 0\\ \beta \gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix}\vspace{3pt}\\ \stackrel{?}{=} \begin{pmatrix} \gamma & \beta \gamma & 0 & 0\\ \beta \gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \gamma & -\beta \gamma & 0 & 0\\ \beta \gamma & -\gamma & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x^0 \\ -x^1 \\ -x^2 \\ -x^3 \end{pmatrix}$

過程を省略しますが、右辺の1番目と2番目の行列の積は$\eta_{\mu \nu}$になります。

$\begin{pmatrix} \gamma & \beta \gamma & 0 & 0\\ \beta \gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix}\vspace{3pt}\\ \stackrel{?}{=} \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x^0 \\ -x^1 \\ -x^2 \\ -x^3 \end{pmatrix}$

右辺のベクトルも$\eta^{\mu\nu}$との積によって1-3行目の符号が反転します。

ここで左辺と右辺を入れ替えます。

(19) $\begin{pmatrix} x^0 \\ x^1 \\ x^2 \\ x^3 \end{pmatrix} = \begin{pmatrix} \gamma & \beta \gamma & 0 & 0\\ \beta \gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x'^0 \\ x'^1 \\ x'^2 \\ x'^3 \end{pmatrix}$

これはローレンツ逆変換そのものです。$ (19) $の等号が成り立つので遡って$ (18) $の等号も成り立ちます。$ (18) $は共変ベクトルの条件でした。したがって、ここで用いられた$ (x_0, -x_1, -x_2, -x_3) $は共変ベクトルです。

補足します。

座標変換の規則に従って$ ( x^0, x^1, x^2, x^3) $を変換すると$ ( x’^0, x’^1, x’^2, x’^3) $になります。したがってこれは反変ベクトルです。しかし全てのベクトルがこの関係になるわけではありません。$ ( x_0, -x_1, -x_2, -x_3) $を変換しても$ ( x’_0, -x’_1, -x’_2, -x’_3) $とはならないのでこれは反変ベクトルではありません。

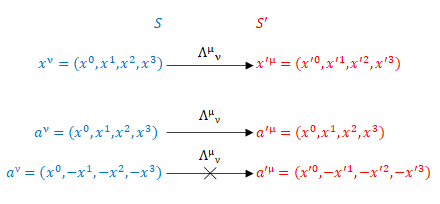
一方で、座標の逆変換の規則通りに$ ( x_0, x_1, x_2, x_3) $を変換すると$ ( x’_0, x’_1, x’_2, x’_3) $にはならないのでこれは共変ベクトルではありません。しかし$ ( x_0, -x_1, -x_2, -x_3) $を変換すると$ ( x’_0, -x’_1, -x’_2, -x’_3) $になります。したがってこれは共変ベクトルです。

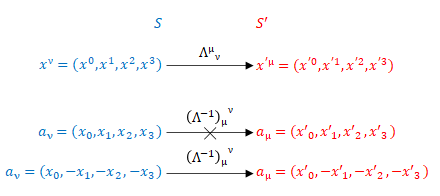
3 まとめ

・反変ベクトル・共変ベクトルは偏微分を使って以下のように定義できます。

反変ベクトル

$$a’^{\mu} = \frac {\partial x’^{\mu}} {\partial x ^{\nu}} a^{\nu}$$

共変ベクトル

$$a’_{\mu} = \frac {\partial x^{\nu}} {\partial x’ ^{\mu}} a_{\nu}$$

・座標変換の係数（$k^{\mu}_{\ \ \nu}$）を使うと以下のように定義できます。

反変ベクトル

$$a’^{\mu} = k^{\mu}_{\ \ \nu} a^{\nu} $$

共変ベクトル

$$a’_{\mu} = \left( k^{-1} \right) _{\mu}^{\ \ \nu} a_{\nu}$$

・$ (x^0, x^1, x^2, x^3) $は以下が成立するので反変ベクトルです。

$$(x’^0, x’^1, x’^2, x’^3) = k^{\mu}_{\ \ \nu} (x^0, x^1, x^2, x^3) $$

・$ (x_0, -x_1, -x_2, -x_3) $は以下が成立するので共変ベクトルです。

$$(x’_0, -x’_1, -x’_2, -x’_3) = \left( k^{-1} \right) _{\mu}^{\ \ \nu} (x_0, -x_1, -x_2, -x_3) $$