相対性理論は我々の直感を裏切る様々な現象を示しています。その出発点となるのが光速度不変の原理です。アインシュタインらの科学者は実験により得られたこの事実より理論的にニュートン力学を覆す法則を導いていきました。本ページでは光速度不変の法則から「時間の遅れ」、「ローレンツ収縮」がどのように導かれるかを考えましましょう。
0 予備知識、説明の順序について
0.1 特殊相対性理論と一般相対性理論
アインシュタインは1905年に特殊相対性理論、1915年に一般相対性理論を発表しました。相対性理論といえばこの両方を指します。
特殊相対性理論とは、2つの異なる慣性系(次節)の間で観測される現象について述べた理論です。時間の遅れ、ローレンツ収縮などは特殊相対性理論によって導かれます。
一般相対性理論とは重力による時空の歪みを記述した理論です。重力レンズや近年少し話題になったスカイツリーと地上の時間の進み方のずれなどはこの理論によって示されます。
本ページでは特殊相対性理論について述べます。
0.2 慣性系
電車の車両内に置かれているボールの動きによって、電車がどのような状態にあるかを考えてみます。
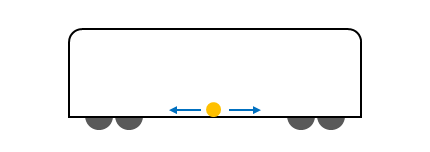
もし、ボールが静止しておらず、かつボールが電車の進行方向に向かって加速していた場合、電車は減速しています。逆にボールが進行方向とは反対方向へ加速していた場合は、電車は加速しています。これらはどちらも電車に加速度が生じている状態です。
もし、ボールが静止している、あるいは等速直線運動をしている場合は、電車も静止しているか等速直線運動をしています。この車両が慣性系です。
つまり、物体に外から力を加えない限りその物体が静止または等速直線運動を続ける座標系を慣性系とよびます。
単にある観測者から見て静止または等速直線運動をする座標系と定義すればよいのではないでしょうか。しかし観測者がいる座標系自体が加速していた場合は観測者が静止または等速直線運動をしている別の座標系を慣性系とは判断できません。
そこで座標系が加速しているかどうかによってそれが慣性系か非慣性系かを区別する必要があります。物体が静止または等速直線運動を続けている場合、その座標系には加速度はないと判断できるからこのような定義になります。
0.3 呼称
本ページでは例として慣性系の名を\(S\)と\(S’\)にします。慣性系\(S\)と\(S’\)に静止している観測者もそれぞれ\(S\)、\(S’\)とよぶことにします。「\(S\)から見て」「\(S’\)から見て」という表現を使いますが、それぞれの観測者から見ているという意味だと考えてください。
また、観測者が静止している慣性系を「静止系」、観測者から見て移動している慣性系を「移動系」とよぶことがあります。相対性理論においては「絶対静止系」は存在しないとされますが、ここでの静止系はその意味ではない点に注意してください。
0.4 説明の順序
「時間の遅れ」と「ローレンツ収縮」は「光速度不変の原理」から直接導くことができますが、次ページで説明する「ローレンツ変換」からも同じようにこれらが成立することが確認できます。
本ページではこれらの現象をなるべく直観的に理解できるよう、ローレンツ変換を使わずに時間の遅れとローレンツ収縮が成立することを説明します。
1 光速度不変の原理
本章では慣性系\(S’\)からボールを投げた場合と、光を照射した場合のそれぞれの速度が、慣性系\(S\)から見てどう異なるかについて述べます。
1.1 慣性系\(S’\)からボールを投げた場合
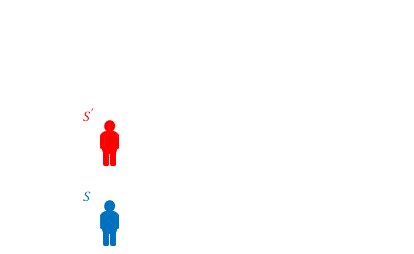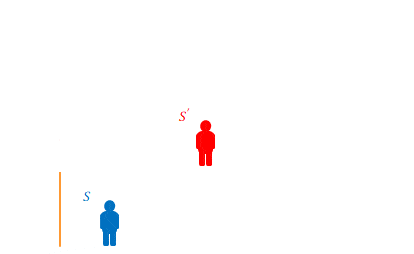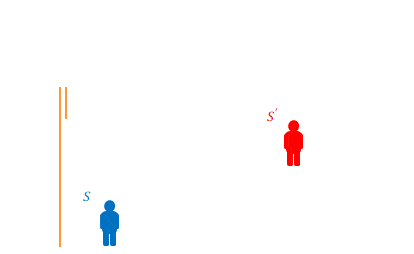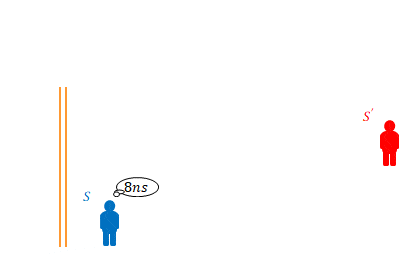
下の図のボールを投げている人(赤色)は\(S’\)、直立でいる人(青色)は\(S\)です。
\(S\)から見て\(S’\)は\(50km/h\)の速度で移動しています。
\(S’\)は進行方向へ向かって\(100km/h\)の速度で投げました。重力の影響は無視してください。
\(S’\)から見るとボールはもちろん\(100km/h\)で移動します。\(S\)から見ると\(150km/h\)で移動します。

1.2 慣性系\(S’\)から光を照射した場合
次にボールではなく、光を\(S’\)から進行方向へ照射したとします。
光速度は約\(3 \times 10^8 m / s\)です。\(S’\)からみた光の先端の速度は\(3 \times 10^8 m / s\)です。
では\(S\)からみた速度はどれだけでしょう。
\(3 \times 10^8 m / s\)です。
前節のボールの例では\(S\)から見たボールの速度は\(S’\)が投げたボールの速度に系の相対速度(\(50km/h\)が加算されますが、本節の例の場合、\(S\)から見た光の速度も\(3 \times 10^8 m / s\)で全く同じです。

これが光速度不変の原理です。
つまり、光の速度は観測する慣性系に関わらず一定の速度であるという原理です。
※ここでは\(S’\)から光を放射したことにしましたが、これが\(S\)からの放射であったとしても両者から見た光の速度はやはり変わりません。ボールの例であれば、どの慣性系から投げるかによって観測される速度は変わりますが、光の場合は照射をする系にも依存しません。
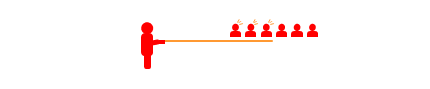
※ここで問題としているのは光の先端の移動速度です。もし観測者が1人しかいない場合、実際には観測者に反射した光が届くまでの時間が追加されることになります。そうではなく、経路に観測者が複数存在し、光が通過した時間を計測することにより光の先端の速度は正確に計測できるものとします。
2 時間の遅れ
ニュートン力学では慣性系によって時間の進み方が変わるということはありませんが、特殊相対性理論では光速度不変の原理に基づいているため、時間の進み方の考え方が変わります。どのように変わるのでしょう。
※ 以降、どちらの慣性系の現象なのか、どちらの慣性系から観測したのか、混乱しやすいので注意してください。
2.1 慣性系による光の到達の比較
慣性系\(S\)から見て慣性系\(S’\)が水平に移動しています。その相対速度を\(v\)とします。
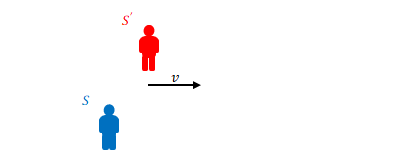
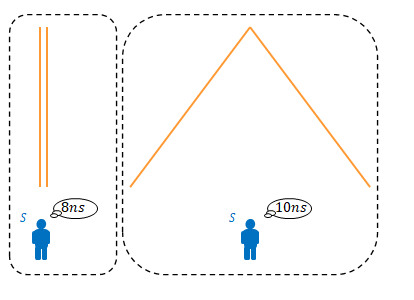
\(S’\)の床から天井に向けて垂直に光を放ちます。光は天井の鏡で反射します。この時間が\(8ns\)であったとします。\(ns\)とは\(10^{-9}\)秒のことです。
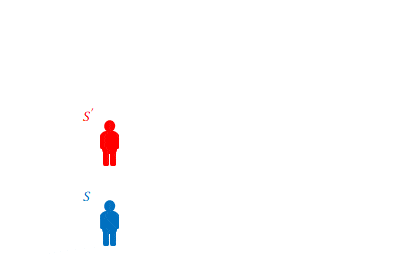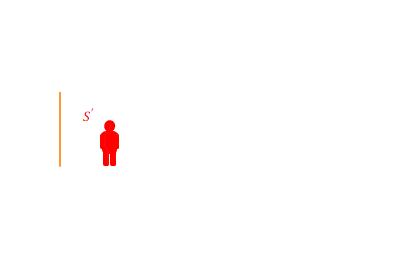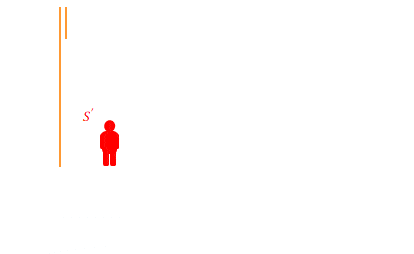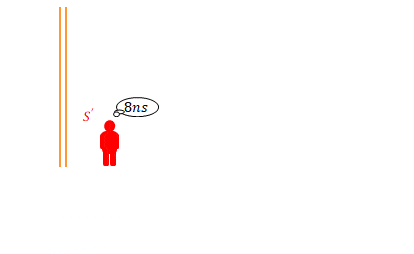
\(S\)から見るとこの時間はどれだけでしょう。

我々の直観では同じ\(8ns\)ですが、特殊相対性理論によれば、そうはなりません。
どう異なるのでしょう。
2.2 光の経路の長さの比較
下の図は両者の光の軌跡を比較したところです。左側は\(S’\)から見た場合、右側は\(S\)から見た場合です。
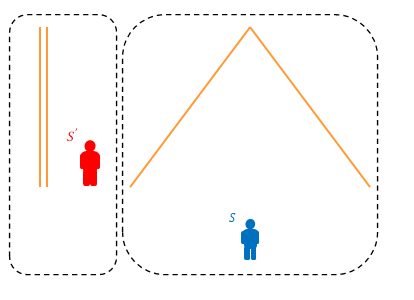
この軌跡の違いが時間の遅れに関係ありそうです。しかし、今比較したいのは以下の違いです。
・\(S\)から見た\(S\)の時間
・\(S\)から見た\(S’\)の時間
ところが上の図の左側は\(S’\)から光を見ています。
そこで、\(S’\)ではなく\(S\)から見て床から天井に向かって垂直に照射した場合を考えます。
光が進んだ距離や床から発して床に届くまでの時間は、明らかに前述の\(S’\)から見て垂直に光が照射された場合と同じです。
そこで、これを入れ替えて下の図のように\(S\)から見て垂直に光が照射された場合と斜めに照射された場合の比較にします。
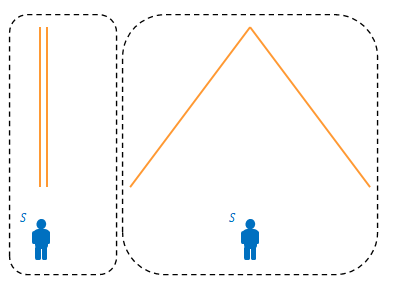
さて、両者の床から照射し反射した光の進んだ距離は違うでしょうか。当然斜めに進んだ場合のほうが長くなります。よく考えると「天井の高さが両者で同じか」という疑問はありますが、ここでは変わらないものとして進めます。このことについては次章で確認します。
一方、前章の通り光の速度は変わりません。放ったのが光ではなくボールであれば斜めに進むほうは速度が大きくなります。しかし光の場合はそうはなりません。
光の進んだ距離は変わるのに光の速度が変わらないということはどういうことでしょう。
到達するまでの時間が異なるのです。
2.3 到達時間の比較
到達時間の違いをもう少し考えてみましょう。
前節まで、光が反射して床に帰ってくるまでを考えていましたが、線対称なのでここからは片側だけに注目します。
まず、垂直な光の線と斜めの線をつなぎ合わせます。
図の区切りは\(1ns\)の間隔を示しています。
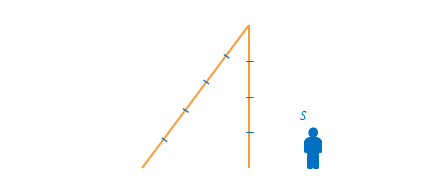
さらに、底辺を追加しを定義し直角三角形を形成します。
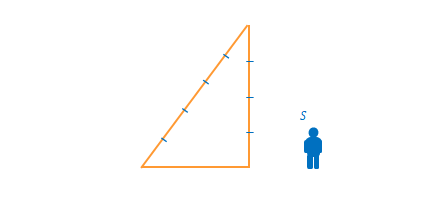
垂直な光の到達時間を\(\Delta t\)、斜めの光の到達時間を\(\Delta t’\)とします。どちらも\(S\)から見た時間であることに注意してください。
直角三角形の各辺の長さは以下で表すことができます。
垂直な辺
\(S\)から見て垂直になるよう放った光が天井に届くまでの距離です。速度は\(c\)、到達までの時間は\(\Delta t\)なので、距離は\(c \Delta t)です。
斜めの辺
\(S’\)から見て垂直になるよう放った光を\(S\)で観測した場合の距離です。速度は\(c\)、到達までの時間は\(\Delta t\)なので、距離は\(c \Delta t’\)です。
底辺
\(S\)から見て、\(S’\)の床にある光源から放った光が天井に届くまでに光が水平方向に移動した距離です。\(S\)と\(S’\)の相対速度は\(v\)、到達までの時間は\(\Delta t’\)なので、距離は\(v \Delta t’\)です。
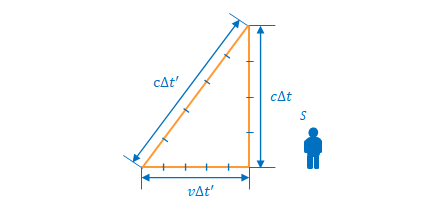
以上より\(\Delta t\)と\(\Delta t’\)の関係を求めることができます。
三平方の定理を適用し、
$$c^2 \Delta t’^{2} = v^2\Delta t^2 + c^2 \Delta t^2 $$
変形し、
$$ \Delta t’ = \frac {1} {\sqrt {1-\frac{v^2}{c^2}}} \Delta t $$
となります。
これが時間の遅れを示しています。
2.4 式の意味
この式の意味を確認しましょう。
前述の通り、慣性系によって光の進む距離が違って見えるため、慣性系の時間の進み方が異なります。\(c \Delta t\)は\(S\)から見て垂直に進む光の距離です。\(c \Delta t’\)は\(S’\)から見ると垂直に進む光を\(S\)から見ているために長くなっています。
したがって\(\Delta t\)と\(\Delta t’\)は2つの事象間の時間で、前者は\(S\)、後者は\(S’\)におけるものであることを示しています。事象とはこの場合、光が床から放出された瞬間と光が天井に到達した瞬間です。
式の右辺の係数は\(S’\)の時間がどれだけ遅れているかを示しています。\(v=0\)では式の右辺の係数は\(1\)なので\(S\)と\(S’\)の時間は同じです。\(v \gt 0\)では係数が\(1\)より大きくなるので\(S’\)の時間は遅れます。\(v\)が大きくなるほど\(S’\)の時間の遅れは大きくなります。
「遅れ」という言葉を使いますが、事象の時刻が一定時間ずれるという意味ではなく、事象間の時間が伸長するという意味である点に注意してください。
ビデオレコーダーで例えるなら「タイムシフト」ではなく「3倍速再生」のようなものです。実際、(極端な場合は)\(S\)から見ると\(S’\)がスローモーションのように見えます。しかし\(S’\)にいる人はそのことを意識しません。
\(S\)から見ると\(S’\)の時計も遅れます。その遅れは累積していきます。
この時間の進み方は時間間隔ともよばれます。移動する慣性系の時間間隔は静止している慣性系から見て長く(大きく)なります。
2.5 単位時間の比較
時間の遅れの式は2つの事象間の時間が別の慣性系(例では\(S’\))では遅れることを示しています。これは\(S’\)の時計が遅れることでもあります。どれぐらい遅れるかというと、その割合は\(\displaystyle \frac {1} {\sqrt {1-\frac{v^2}{c^2}}} \)倍です。
これを本章の例で確認してみましょう。
2.3節の図では\(1ns\)ごとの区切りを入れましたが、これらは\(S\)の時間です。斜めに進む光の到達時間は\(5ns\)でした。しかし\(S’\)から見ると、この光は垂直に進んでおり、\(4ns\)しかかかっていません。区切りを赤で追加すると以下のように間延びしています。
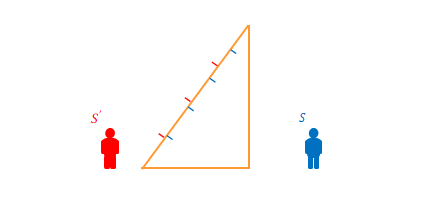
水平にすると下の図のようになります。
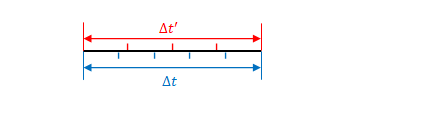
それぞれの単位時間(\(1s\))で比較するとやはり同じ比率になります。
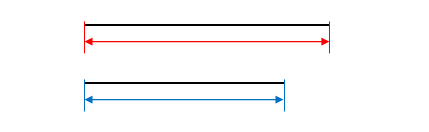
計算するまでもなく、\(S’\)における\(1s\)は\(S\)における\(\displaystyle \frac {1} {\sqrt {1-\frac{v^2}{c^2}}} [s]\)です。この例であれば\(1.25s\)です。
3 ローレンツ収縮
3.1 なぜ長さが収縮する?
前章では慣性系の相対運動による時間の遅れについて述べました。しかし系によって変わるのは時間だけではありません。距離も変化します。
図のように\(S\)と\(S’\)から棒を観測しています。
まず、\(S\)から見て\(S’\)と棒も静止している場合を考えます。
両者から見た棒の長さは当然同じです。これを\(l_{0}\)とします。
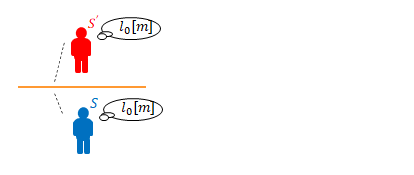
次に\(S’\)が移動する場合を考えます。棒は\(S’\)から見て静止しています。棒は進行方向と平行に置かれています。
説明のため、\(S\)の空間に縦線を2本追加します。
棒の右端が左の縦線を通過した瞬間を\(0[s]\)とします。
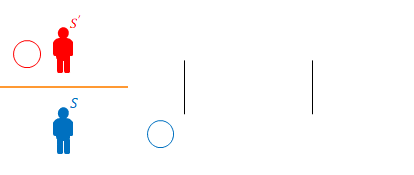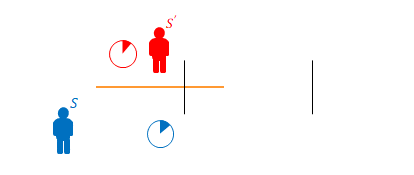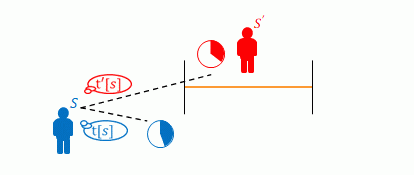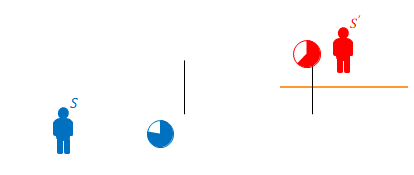
棒の右端が右の縦線を通過する瞬間を以下とします。
\(S\)が\(S\)に静止する時計で測った時間:\(t[s]\)
\(S\)が\(S’\)に静止する時計で測った時間:\(t'[s]\)
長さ・速度・時間の関係より棒の長さを以下のように求めることができます。\(v\)は相対速度(\(s\)から見た速度)です。
\(S\)から見た棒の長さ:
$$l=vt$$
\(S’\)から見た棒の長さ:
$$l_{0}=vt’$$
\(t\)と\(t’\)は「時間の遅れ」の効果により以下の関係になります。
$$t’=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}t$$
以上より\(l\)と\(l_{0}\)の関係が求められます。
$$l=\sqrt{1-\frac{v^2}{c^2}}l_{0}$$
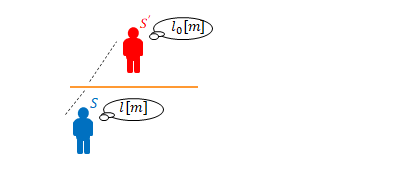
\(l_0\)は\(S’\)から見た長さですが、棒が静止しているときの\(S\)から見た長さでもあります。
つまりこの式は静止しているときと動いているときの棒の長さの見え方の関係を示しています。右辺の係数は必ず\(1\)以下で、速度が大きいほど小さい値になります。つまり、移動の速さに応じて棒が縮んで見えます。
これをローレンツ収縮とよびます。
ところで、ここでは棒が\(S\)から見て静止している、ある点を通る速度と時間の積から長さを求めました。ある瞬間における2点間の距離を求めているわけではありませんが、正しいでしょうか。
前章の通り、時間の遅れは\(c\)と\(v\)のみによって決まる値を係数とする比例の関係で表されます。もし時間の遅れの係数が時間や位置によって変わるのであれば上記のようには求められませんが、比例定数は時間や位置に依存しません。ローレンツ収縮が時間の遅れに起因するものであるとするのであれば時間と速度の積を長さとして求めることに問題はないはずです。
3.2 移動方向以外の長さは収縮する?
前節では移動方向を向いている棒が収縮することについて述べました。
では移動方向と垂直な方向を向いている棒は収縮するのでしょうか。
図のように縦方向に棒があるとします。\(S’\)と棒は右方向へ移動します。
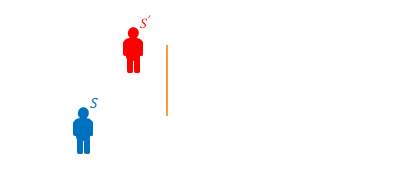
棒はどれだけ縮むでしょう。
前節ではある点を通過する時間から長さを求めました。しかしこの場合は通過する時間を定義できません。
つまり\(l_0\)と\(l\)の関係を導くことはできません。
棒が移動方向を向いていた場合は両者の関係が成立しましたが、これは長さに関する制約が存在するということです。
移動方向と垂直な棒にはこのような制約は存在しません。この場合は棒の長さは変化しないはずです。
したがって、ローレンツ収縮は慣性系の移動方向にのみ生じます。
2.2節で、移動方向とは垂直な距離は慣性系によって変わらないこととしましたが、ローレンツ収縮が起きないので確かにこの仮説の通りです。
4 まとめ
・ある慣性系から放たれた光を別の慣性系から観測しても同じ速度です。これを光速度不変の原理とよびます。
・静止系に対し速度\(v\)で移動する慣性系の時計を静止系から観測すると時間間隔は\(\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)倍になり、必ず遅れます。これを時間の遅れとよびます。
・静止系に対し速度\(v\)で移動する物体の進行方向の寸法は、これを静止した状態で観測した場合に比べて\(\displaystyle \sqrt{1-\frac{v^2}{c^2}}\)倍になり、必ず収縮します。これをローレンツ収縮とよびます。
