1次元波動方程式

1次元波動方程式とは時間経過とともに直線上を両方向に移動する波を表した方程式です。波とは、例えば水面上を伝わる波、音波、電磁波などです。

ここでは波動方程式およびその解のもつ意味と解の求め方説明します。

1 1次元波動方程式の定義と一般解

1.1 波動とは？

波動を理解するうえで少しだけ注意すべきところがあります。

以下の2つのグラフの違いは何でしょう。

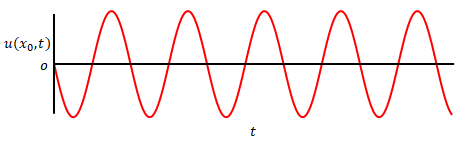
横軸が$x$か$t$かの違いですね。この場合の$x$は位置、$t$は時間を示す変数、またグラフ縦軸の$x_0$、$t_0$は定数です。

波動は位置と時間の両方の変数をもつ多変数関数であるという点に注意してください。

1.2 1次元波動方程式の定義

1次元波動方程式（以下波動方程式）は次のように定義されます。

$$\frac {\partial^2 u} {\partial t^2} = c^2 \frac {\partial ^2 u} {\partial x^2}$$

$x$は位置、$t$は時刻を表す変数、$c$は速度を表す定数で、本ページでは$c>0$とします。

1.3 移流方程式と物理的意味

後で述べる一般解があれば$u$がどのような挙動をするかは簡単にわかるのですが、一般解がわからなくても波動方程式より直観的に理解することができます。

そこでまずは移流方程式について簡単に説明します。

移流方程式と波動方程式は別のものです。本ページの目的は波動方程式の説明なのですが、次節で波動方程式の物理的意味を述べるため、予備知識として移流方程式について簡単に触れます。

移流方程式は以下の式で定義されます。

$$\frac {\partial u} {\partial t} = -c \frac {\partial u} {\partial x}$$

移流方程式も波動方程式も関数の移動を示すものです。波動方程式は正負両方向へ同じ大きさの速度で（正負方向が同じ波形とは限りませんが）移動する状態を記述しています。これに対し移流方程式は$c$で定義される方向へのみ関数が移動する状態を示しています。

$t=0$において$u(x,t)$が下の図のような状態であったとします。横軸は$x$です。

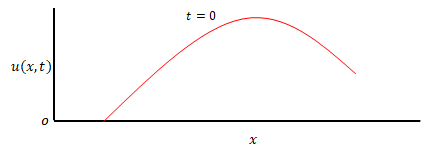
$t=\Delta t$に図のように移動していたとします。

$t=0$から$t=\Delta t$までの間の$u(x,t)$の変化を$\Delta u$とします。

また、$t=0$から$t=\Delta t$の間に$\Delta x$だけ移動していたとします。

$u(x,t)$の移動速度を$c$とすると、以下のように表すことができます。

$$\Delta x = c \Delta t$$

また、$u(x,t)$の$x$軸における傾きは$\displaystyle \frac {\partial u(x, t) } {\partial x} $なので、

$$\Delta u = -\frac {\partial u(x, t)} {\partial x} \Delta x $$

となります。下の図のように$u(x,t)$に線を追加すれば$\Delta x$、$\Delta t$と傾きの関係が確認できます。

右辺と左辺の符号が逆になる点に注意してください。下の図の場合、$\Delta x$が正ですが、$\displaystyle \frac {\Delta u} {\Delta x}$も正ですが、$\Delta u$は負です。

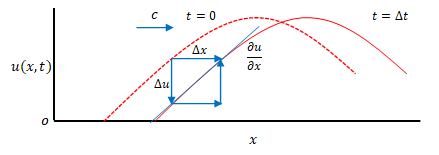
変数を移動し、

$$ \frac {\partial u(x, t)} {\partial x} = -c \frac {\Delta u} {\Delta x} $$

$\Delta t$が無限小であるとすれば$\Delta x$も無限小となり、右辺は偏微分とみなすことができます。したがって、

$$\frac {\partial u} {\partial t} = -c \frac {\partial u} {\partial x}$$

となり定義と一致します。

つまり移流方程式は$u(x,t)$全体が速度$c$で移動することを示しています。

1.4 波動方程式の物理的意味

前節では移流方程式における速度がどう表されるかを確認しました。これを元に、波動方程式における速度がどう表されるかを考えましょう。

波動方程式を変形します。

$$\frac {\partial^2 } {\partial t^2} u – c^2 \frac {\partial ^2 } {\partial x^2} u = 0$$

$$\left (\frac {\partial } {\partial t} + c \frac {\partial } {\partial x} \right ) \left (\frac {\partial } {\partial t} – c \frac {\partial } {\partial x} \right ) u = 0$$

2つの方程式に分けることができます。

$$\frac {\partial u} {\partial t} + c \frac {\partial u} {\partial x} = 0$$

$$\frac {\partial u} {\partial t} – c \frac {\partial u} {\partial x} = 0 $$

1番目の式は移流方程式と同じです。2番目の式も$c$の符号以外は同じです。波動方程式の解は$c$の速さで$u(x,t)$全体が左右に移動することを示しています。

また、移流方程式にもいえることですが、この式は$x$、$t$がどのような値であっても成立します。ということは、横軸を$x$とした波形は時間経過とともに移動しても常に一定だということです。

1.5 波動方程式の一般解

前節で波動方程式の移動速度について述べました。これを式にすると以下です。

$$u(x,t)=f(x-ct)+g(x+ct)$$

$f$と$g$は任意の関数です。ただし微分可能かつ1階導関数（1度微分して得られる関数）は連続であることが条件です。

波動方程式は、それ単独では一意に解が決まりません。範囲をもった解として表されます。これを一般解とよびます。波動方程式の一般解はダランベールの解ともよばれます。

前節では波動方程式が波の移動を示していると述べましたが、解には触れていませんでした。ここで解の意味を考えてみましょう。

下の図は横軸が$x$です。$f(x-ct)$を示しています。括弧の中の$t$の項の符号が負なので時間経過とともに波は右へ移動します。

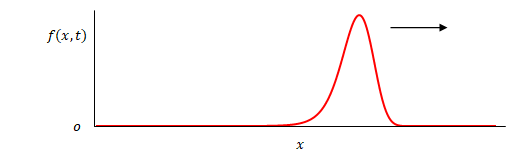
次の図は$g(x+ct)$です。$t$の項が正なので左へ移動します。

$u$は$f(x-ct)$と$g(x+ct)$を重ね合わせた波形です。つまり解は左右に速度$c$で移動する任意の波の和ということになります。

2 変数変換による解法（ダランベールの解・式）

2.1 一般解（ダランベールの解）

波動方程式の一般解が$u=f(x-ct)+g(x+ct)$であることを確認しましょう。1.4節の手順と重複するところが多いのですが、以下の解法はよく知られているので最初から述べます。

波動方程式を以下のように変形します。

$$ \left ( \frac {\partial u}{\partial x} – \frac {1}{c} \frac {\partial u}{\partial t} \right ) \left ( \frac {\partial u}{\partial x} + \frac {1}{c} \frac {\partial u}{\partial t} \right ) = 0 \tag { 1 } $$

括弧の中を簡単に表すため、以下のように変数を定義します。

$$ \xi = x – ct $$

$$ \eta = x + ct $$

合成関数の微分の公式を用いると偏微分は、

$$\frac {\partial u}{\partial x} = \frac {\partial u}{\partial \xi} \frac {\partial \xi} {\partial x} + \frac {\partial u}{\partial \eta} \frac {\partial \eta} {\partial x}$$

$$\frac {\partial u}{\partial t} = \frac {\partial u}{\partial \xi} \frac {\partial \xi} {\partial t} + \frac {\partial u}{\partial \eta} \frac {\partial \eta} {\partial t}$$

定義より、

$$\frac {\partial \xi }{\partial x} = 1, \frac {\partial \eta }{\partial x} = 1, \frac {\partial \xi }{\partial t} = -c, \frac {\partial \eta }{\partial t} = c$$

これを代入すると、

$$ \frac {\partial u}{\partial \xi} = \frac {\partial u}{\partial x} – \frac {1}{c} \frac {\partial u}{\partial t}$$

$$ \frac {\partial u}{\partial \eta} = \frac {\partial u}{\partial x} + \frac {1}{c} \frac {\partial u}{\partial t} $$

この2式を$ (1) $に代入すると、

$$\frac {\partial^2 u}{\partial \xi \partial \eta } = 0$$

が得られます。

変数を変換することにより波動方程式は簡単な形式にすることができました。

直観的には$\displaystyle \frac {\partial^2 u}{\partial \xi \partial \eta } = 0 $ということは $\displaystyle \frac {\partial u}{\partial \xi}$と $ \displaystyle \frac {\partial u}{\partial \eta}$ のどちらかが0ということであり、$u$は$\xi$のみの関数と$\eta$のみの関数の和で構成されるはずです。つまり

$$u = f(\xi) + g(\eta)$$

となります。

確認のため、$\displaystyle \frac {\partial^2 u}{\partial \xi \partial \eta } = 0$を積分してみます。まず$\xi$で積分すると、$h$を用いて

$$ \frac {\partial u}{\partial \eta} = h(\eta)$$

と表すことができます。

さらに$\eta$で積分すると、

$$ u = \int h(\eta) d\xi + f(\xi) $$

となりますが、$h(\eta)$を$\xi$で積分しても$\eta$の関数であることに変わりはないので、これを$g$として、

$$u = f(\xi) + g(\eta) $$

とすることができます。やはり同じ結果でした。

$x$と$t$で表すと、

$$u = f(x – ct) + g(x + ct) $$

となります。

1.3節と同じ結果になりました。

波動方程式の一般解はダランベールの解とよぶこともあります。

2.2 初期値問題（ダランベールの式）

2.1節で求めたのは一般解の解法でした。

一方、例えば、境界条件（特定の$x$における$u$の値）や初期条件（特定の$t$における$u$の値）などが追加されることにより解の範囲が限定されます。

その一つがダランベールの式です。

ダランベールの式では以下のように初期条件を定めます。

$$u(x,0)=u_0(x) \tag { 1 }$$

$$\left . \frac {\partial u(x,t)} {\partial t} \right |_{t=0} = u_1(x) \tag { 2 }$$

※バーティカルバー（縦線）は関数を評価する条件を示します。この場合の左辺は$u(x,t)$を$t$について偏微分をし、$t=0$を代入した式という意味です。

以下が解法です。

$ (1) $に$ \left . u(x, 0) = \left (f(x-ct) + g(x+ct) \right ) \right |_{t = 0} $を代入すると、

$$u_0(x) = f(x)+g(x) \tag { 3 } $$

$ (2) $に$ u(x,0)= \left . \left ( f(\xi)+q(\eta) \right ) \right |_{t=0} $を代入すると、

$$u_1(x) = \left . \frac {\partial u(x,t)} {\partial t} \right |_{t=0} = \left . \left (\frac{\partial f(\xi)} {\partial t} + \frac{\partial g(\eta)} {\partial t} \right ) \right|_{t=0} \tag { 4 }$$

第1項を変形します。

合成関数の微分の公式より、

$$\displaystyle \frac {\partial f(\xi)}{\partial t} = \frac {\partial f(\xi)}{\partial \xi } \frac {\partial \xi} {\partial t} $$

$\xi = x -ct$なので

$$\displaystyle \frac {\partial \xi}{\partial t} = -c$$

これを上の式に代入し、

$$\displaystyle \frac {\partial f(\xi)}{\partial t} = -c \frac {\partial f(\xi)}{\partial \xi }$$

$t=0$において$\xi= x$なので、

$$\left . \frac{\partial f(\xi)} {\partial \xi} \right|_{t=0} = c \frac {\partial f(x)} {\partial x} $$

同様に、

$$\left . \frac{\partial g(\eta)} {\partial t} \right|_{t=0} = c \frac {\partial g(x)} {\partial x} $$

これらを$ (4) $に代入すると、

$$u_1(x) = -c \frac {\partial f(x)} {\partial x} +c \frac {\partial g(x)} {\partial x} \tag { 5 }$$

$ (5) $の$c$を左辺に移動し$-\infty$から$x$までの区間で積分すると、

$$ \frac {1}{c} \int_{-\infty} ^x u_1(y) dy = -f(x) + g(x) + C \tag { 6 }$$

$C$は積分定数です。積分区間の$x$と区別するために新たに$y$を使い積分しています。

$ (6) $と下記$ (3) $より$f(x)$と$g(x)$を求めます。

$$u_0(x) = f(x)+g(x) \tag { 3 }$$

$$\frac {(3) – (6)} {2} =f(x)=\frac {1}{2} \left ( u_0(x) – \frac {1}{c} \int_{-\infty} ^x u_1(y) dy – C \right ) \tag { 7 }$$

$$\frac {(3) + (6)} {2} =g(x)=\frac {1}{2} \left ( u_0(x) + \frac {1}{c} \int_{-\infty} ^x u_1(y) dy + C \right ) \tag { 8 }$$

これらを

$$ u(x,t) = f(x-ct) + g(x+ct) $$

に適用し$ (7) $の$x$を$x-ct$、$ (8) $の$x$を$x+ct$に置き換えます。

定積分の演算は以下のように変えることができる点に注意ください。

$$\int_a^b j(r) dr – \int_a^c j(r)dr = \int_c^b j(r) dr$$

$u(x,t)$は以下になります。

$$u(x,t)=\frac {1}{2} \left \{ u_0(x-ct) + u_0(x+ct) \right \} + \frac {1}{2c} \int_{x-ct} ^{x+ct} u_1(y) dy $$

この解をダランベールの式とよびます。

2.3 ダランベールの式の物理的意味

ダランベールの式の

$$ \frac {1}{2} \left \{ u_0(x-ct) + u_0(x+ct) \right \} $$

の部分だけをみると一般解（ダランベールの解）とあまり変わらないように思えます。

しかし$u_0$は初期条件として与えられているものであり、一意に決まる点が大きく違います。

また、この部分からは時間経過とともに$x$軸を右へ移動する成分と左へ移動する成分が同じで、$u(x,0)$のそれぞれ半分の大きさであることがわかります。

ではこの項はどのような動きをするのでしょうか。

$$\frac {1}{2c} \int_{x-ct} ^{x+ct} u_1(y) dy $$

$u_1(x)$が$u(x,t)$の$t=0$における時間微分であることから、これが初速を表すもののように思えます。そこで1.3節で述べた移流方程式を適用することにします。

$$\frac {\partial u} {\partial t} = -v \frac {\partial u} {\partial x}$$

これは初期条件を追加していることになります。元の条件では$t=0$における時間微分は$u_1(x)$という関数である、というだけでしたが、移流方程式に従うということはすべての$x$において時間微分が$\displaystyle -v \frac {\partial u} {\partial x}$であるという制約が追加されます。

なお、この条件は$t=0$のみに適用される点、初速は$c$である必要はないので$v$に変えている点、移流方程式なので速度は1方向のみである点に注意ください。

元の初期条件の$ (2) $の$x$を$y$に変えます。

$$\left . \frac {\partial u(y,t)} {\partial t} \right |_{t=0} = u_1(y) $$

移流方程式を代入すると

$$\left . \frac {\partial u(y,t)} {\partial t} \right |_{t=0} = -v \frac {\partial u(y,t)} {\partial y}$$

より、

$$u_1(y) = -v \frac {\partial u(y,t)} {\partial y}$$

これを$x-ct$から$x+ct$で積分し$\displaystyle \frac{1}{2c}$を係数として追加します。

$$\frac {1}{2c} \int_{x-ct} ^{x+ct} u_1(y) dy = \frac {1}{2c} \int_{x-ct} ^{x+ct} \left (-v \frac {\partial u} {\partial y} \right )dy$$

$y$で偏微分した後で積分をしているので単なる積分区間2点での引き算になります。

$$\frac {-v} {2c} \{ u(x+ct) – u(x-ct) \} = \frac{v}{2c} \{u(x-ct) – u(x+ct) \}$$

ダランベールの式を書き直すと、

$$u(x,t)=\frac {1}{2} \left \{ u_0(x-ct) + u_0(x+ct) \right \} + \frac{v}{2c} \{u(x-ct) – u(x+ct) \} $$

となります。あるいは、

$$u(x,t)=\frac {1}{2} \left \{ \left (1+\frac{v}{c} \right) u_0(x-ct) + \left (1-\frac{v}{c} \right) u_0(x+ct) \right \} $$

です。

つまりダランベールの式の積分の項は、右へ移動する波の大きさが$\displaystyle \frac{v}{c}$だけ増え、左へ移動する波の大きさが$\displaystyle \frac{v}{c}$だけ減ることを示しています。

初期条件の移流方程式の$-v$は右へ移動する速さを示しています。$t=0$に初速としてこれが与えられた場合でも$t>0$では波動方程式に従うので、波の移動速度は$\pm c$に代わります。$v$は波の速度には現れてきませんが$u$の大きさに関わります。

本節は仮に初期条件に移流方程式を追加した場合の話であって、元の初期条件だけの場合はこの限りではないことに注意ください。

波形がどのように変化するかは次節で確認ください。

2.4 ダランベールの式のグラフ

ダランベールの式の波形を動的に表してみました。

以下、説明です。

表示

・各段の関数は以下のように定義します。

1段目
$$u(x,0)=u_0(x) $$
2段目
$$e(x,t) = \frac {1}{2} \left ( u_0(x-ct) + u_0(x+ct) \right )$$
3段目
$$\left . \frac {\partial u(x,t)} {\partial t} \right |_{t=0} = u_1(x) $$
4段目
$$h(x,t)= \frac {1}{2c} \int_{x-ct} ^{x+ct} u_1(y) dy $$
5段目
$$u(x,t)=\frac {1}{2} \left ( u_0(x-ct) + u_0(x+ct) \right ) + \frac {1}{2c} \int_{x-ct} ^{x+ct} u_1(y) dy $$

・1段目と3段目が初期条件、2段目と4段目が解（ダランベールの式）の一部、5段目が解です。

・グラフの下に、選択している速さや関数を表示しています。

操作

・「開/止」ボタンを押すと表示更新と停止を交互に切り替えます。
・「速」ボタンを押すと3段階で速さを切り替えます。
・「u_0(x)」ボタンを押すごとに$u_0(x)$を以下のように切り替えます。
三角波 → 矩形波 → 正規分布
・「u_1(x)」ボタンを押すごとに$u_0(x)$を以下のように切り替えます。ここでの微分とは$t$についての微分のことです。
三角波の微分 → 矩形波の微分 → 正規分布の微分
・「u_0(x)」ボタンと「u_1(x)」の組み合わせに制限はありませんが、例えば「三角波」と「三角波の微分」のように合わせると前節のような移流方程式が初期条件に追加された状態になります。

注意点

・波動方程式における一般解を構成する関数は微分可能かつ1階導関数は連続していなければならないという条件があるので初期条件に三角波や矩形波を設定できないのですが、なるべくわかりやすい波形としてあえて選びました。ご了解ください。

補足

まず$u_0(x)$と$e(x)$の関係を確認ください。$u_0(x)$が等しい大きさに分かれて左右に移動することがわかります。

次に$u_0(x)$と$e(x)$の関係に注目してください。

$u_0(x)$と$u_1(x)$が無関係（$u_0(x)$が三角波で$u_1(x)$が矩形波の微分など）の場合は$u(x,t)$の波形に意味があるように思えません。

例えば$u_0(x)$を「三角波」、$u_1(x)$を「三角波の微分」というように波形を合わせてください。

$h(x,t)$に$u(x)$と同じ形（縦方向の係数は異なります）の山が2つでき、片方が反転していることがわかります。微分したものを積分しているので同じ関数になりますが、定積分なので片方は上下が反転します。

これと$e(x,t)$との和が$u(x,t)$なので、$u(x,t)$の片方の山は大きく、もう一方の山は小さくなります。

3 変数分離による解法

波動方程式の解が$f(x-ct)$と$g(x+ct)$であるなら、両関数の中に2つの変数が存在するために偏微分が複雑になります。前章ではこれを別の変数に置き換えることにより波動方程式を簡単な形式にすることができました。

本章では変数を置き換えるのではなく、波動方程式を変数（$x$と$t$）ごとの式に分けることによる方法を考えます。

3.1 変数分離

改めて波動方程式です。

$$\frac {\partial^2 u}{\partial t^2} = c^2 \frac {\partial ^2 u} {\partial x^2} $$

$u$を$x$と$t$の関数の積で表すことができるものとし

$$u=X(x)T(t)$$

と表します。※

波動方程式は、

$$X(x)\frac {d^2 T(t)}{d t^2} = c^2 T(t) \frac {d ^2 X(x)} {d x^2} $$

となります。関数と$c^2$を移動し、

$$\frac {1}{c^2T(t)}\frac {d^2 T(t)}{d t^2} = \frac {1}{X(x)} \frac {d ^2 X(x)} {d x^2} $$

と、左辺は$t$の関数、右辺は$x$の関数に分けることができます。

$t$に関する方程式であると考えると右辺は定数になります。また、$x$に関する方程式であると考えると左辺は定数になります。そこで、以下のように$k$を定義し、

$$\frac {1}{c^2T(t)}\frac {d^2 T(t)}{d t^2} = \frac {1}{X(x)} \frac {d ^2 X(x)} {d x^2} =k$$

$x$と$t$を分けて表すことができます。

$$\frac {d ^2 X(x)} {d x^2} =kX(x)$$

$$\frac {d^2 T(t)}{d t^2} =kc^2T(t)$$

2つの微分方程式になりました。

この$k$を分離定数とよびます。

※分離できると仮定していますが本当に可能なのでしょうか。このことについて私は正確に答えられないのですが、少なくとも分離できると決めて得られた解に何の矛盾もないことから、部分的には正しいといえます。

3.2 1階微分方程式

得られた式2つの式はどちらも線形常微分方程式です。「減衰振動」で解いた式と同じ形式の常微分方程式です。ご覧になった方は思い出してください。

このような方程式の場合、特性方程式を解くことにより微分方程式の解が得られるのですが、これを使わずに解いてみましょう。

まず次のような方程式の解は何でしょう。

$$y' = y$$

微分をすると自分自身になる関数です。

指数関数ですね。任意定数を用い、

$$y=Ce^x$$

と表すことができます。

$$y'=ay$$

はどうでしょう。$a$は定数です。微分することにより指数の係数が外に出るので、

$$y=Ce^{ax}$$

です。

以上は1階微分方程式ですが、前節で分離した2階微分方程式については次節で解いてみます。

その前に以下の点、記憶ください。

2階微分方程式の解は1次独立の関係にある解が2つまたは1つあります。2つの場合、1次結合の形式で表すことができます。

例えばある微分方程式の解が$y_1$、$y_2$であり、それらが1次独立であれば解は以下のように表されます。

$$ y = C_1 y_1 + C_2 y_2 $$

1次独立と1次結合の説明をすべきところですが、長くなるので省略します。

次節以降、1次独立であるとし1次結合を適用しているところがあります。

3.3 $ \displaystyle \frac {d ^2 X(x)} {d x^2} =kX(x) $の解

3.1節で分離した方程式の1つである以下について解を求めます。

$$\displaystyle \frac {d ^2 X(x)} {d x^2} =kX(x) $$

解は$k$が正・ゼロ・負のいずれであるかによって異なるのでそれぞれに分けます。

(a)$k > 0$の場合

解は指数関数で表されます。左辺は微分を2度しているので指数部の係数の2乗が外に出ます。これが右辺の$k$と等しいので指数関数の指数部は$k$の平方根です。つまり$\displaystyle e^{\sqrt{k}}$と $\displaystyle e^{-\sqrt{k}}$ が解の一部です。両者は1次独立なので、

$$X(x) = C_1 e^{\sqrt{k}x} + C_2 e^{-\sqrt{k}x} $$

と表されます。

しかしこれでは$k \rightarrow \pm \infty$で$X(x)$が発散します。

確かに解ではあるのですが、物理的に意味のある解ではないのでここでは除外します。

(b) $k = 0$の場合

上述(a)の解に$k = 0$を代入すると

$$X(x) = C_1 + C_2 = C_3 $$

と定数で表すことができます。これは解の一部ではありますが、すべてではありません。

2度微分して0になる関数なので1次式も解になります。したがって、

$$X(x)=C_1 x + C_2 $$

です。しかしこれも発散するので除外します。

上述(a)と同じように指数関数で表すことができます。異なるところは指数部が虚数になるところです。指数部が虚数であればオイラーの公式の通り三角関数に置き換えられます。

$k < 0$なので、平方根は以下のように表します。

$\pm \sqrt{-k} $

このま1次結合によって表すと複素数となります。そこで三角関数を使用して解を表します。

$y=cos x$も$y=sin x$も微分を2度すると符号が反転します。したがって、

$$X(x) = C_1 \cos (\sqrt{-k}x) + C_2 \sin (\sqrt{-k}x) $$

が解です。やや説明を端折りましたが、正しいかどうか確認してみてください。

発散しないので、この条件にて次節以降、さらに解を調べます。

3.4 $\displaystyle \frac {d^2 T(t)}{d t^2} =kc^2T(t)$の解

もう一つの方程式も同様です。

$$\frac {d^2 T(t)}{d t^2} =kc^2T(t)$$

$k < 0$の場合に限定し、前節の$k$を$kc^2$に置き換え、

$$T(t) = C_3 \cos (\sqrt{-k}ct) + C_4 \sin (c\sqrt{-k}ct) $$

です。

3.5 $k<0$の場合の解の物理的意味

次に境界値を追加した場合の解を求めるところですが、その前に境界値がない場合に元の波動方程式の解にどのような意味があるか考えてみます。長い割にはあまり意味のあることをやっているわけでもないのですが、よければ「＋」を押して確認ください。

解の物理的意味

前節まで、分離定数$k$を仮定し、分離した波動方程式のそれぞれの解を求めました。この積が$u(x,t)$の解です。一見すると移動する正弦波のようです。

しかし、解が一意に決まるわけではありません。$k$が負であれば必ず成立します。解は広範囲なはずです。その広範囲な解を$k$を使わずに表すことにします。

まず、解を指数関数で表します。前節では三角関数で表しましたが計算が簡単になるよう改めます。

$k > 0$の場合と同じ形の解になるはずですが、根号の中が負にならないよう、負号をつけ、虚数なので根号の外で$i$をつけます。

$$X(x) = C_1 e^{i \sqrt{-k}x} + C_2 e^{-i \sqrt{-k}x} $$

$$T(t) = C_3 e^{i \sqrt{-k}ct} + C_4 e^{-i \sqrt{-k}ct} $$

これを変数分離の最初で定義した式に適用します。

\begin{align}
u(x,t)&=X(x)T(t)\\
&= C_1 C_3 e^{i \sqrt{-k}x} e^{i \sqrt{-k}ct} \\
&+ C_1 C_4 e^{i \sqrt{-k}x} e^{-i \sqrt{-k}ct}\\
&+ C_2 C_3 e^{-i \sqrt{-k}x} e^{i \sqrt{-k}ct}\\
&+ C_2 C_4 e^{-i \sqrt{-k}x} e^{-i \sqrt{-k}ct}
\end{align}

$C_1$ から$C_4$の積を別の定数に置き換え整理し、

$$u(x,t)=C_{5} e^{i \sqrt{-k} (x – ct)} + C_{6} e^{-i \sqrt{-k} (x – ct)} +C_{7} e^{i \sqrt{-k} (x + ct)} +C_{8} e^{-i \sqrt{-k} (x + ct)} $$

$\xi = x – ct$、$\eta = x + ct$とすると、

$$u(x,t)=C_{5} e^{i \sqrt{-k} \xi} + C_{6} e^{-i \sqrt{-k} \xi} + C_{7} e^{i \sqrt{-k} \eta} + C_{8} e^{-i \sqrt{-k} \eta} $$

$\omega = \sqrt{-k}$とすると、

$$u(x,t)=C_{5} e^{i \omega \xi} + C_{6} e^{-i \omega \xi} + C_{7} e^{i \omega \eta} + C_{8} e^{-i \omega \eta} $$

冒頭で述べたように$k<0$すべてで解は成立します。これらは一次独立です。したがって一次結合で表すことができます。すべての$\omega$における解を一次結合で表すことを考えます。

まず仮に整数$n$を用いて以下のように表します。

$$u(x,t)=\sum_{n=0}^{\infty} (D_{n} e^{i n\omega \xi} + D_{-n} e^{- i n\omega \xi} + E_{n} e^{i n\omega \eta} + E_{-n} e^{-i n\omega \eta})$$

$D_n$と$E_n$は定数です。$n$が正の場合と負の場合をまとめ

$$u(x,t)=\sum_{n=-\infty}^{\infty} (D_{n} e^{i n\omega \xi} + E_{n} e^{i n\omega \eta})$$

と表せます。しかし、$k$の分布は離散的ではありません。連続的です。したがって級数では表すことができません。

そこで、

$$\frac {n}{M} = \omega$$

$$\frac {1}{M} = \Delta \omega$$

と定義し級数に$M \Delta \omega= 1$を掛けます。

$$ u(x,t) = \sum _{n=-\infty}^{\infty} M(D_{n} e^{i n\omega \xi} + E_{n} e^{i n\omega \xi}) \Delta \omega$$

$\Delta \omega$ が無限に小さくなるとすると、

\begin{align}
u(x,t) &=\lim_{\Delta \omega \to 0} \sum_{n=-\infty} ^{\infty}M (D_{n} e^{i n\omega \xi} + E_{n} e^{i n\omega \xi}) \Delta \omega\\
&= \int_{-\infty}^{\infty} D(\omega) e^{i \omega \xi} d\omega + \int_{-\infty}^{\infty} E(\omega) e^{i \omega \eta } d\omega
\end{align}

このように、積分で表すことができます。$D(\omega)$、$E(\omega)$は$M D_n$、$M E_n$を$\omega$の関数にしたものです。

この式に見覚えがないでしょうか。

フーリエ逆変換ですね。

$\displaystyle \frac {1}{2\pi}$の有無は定数の定義で調整できるので気にしないでください。

ここまでの経緯をまとめると以下です。
・波動方程式を変数分離する
・線形微分方程式になる
・$k<0$における解は、指数部が虚数の指数関数になる
・これらの解を1次結合するとフーリエ逆変換になる

$D(\omega)$、$E(\omega)$は元をたどれば微分方程式の解の定数でした。任意の値です。この任意の値で構成されるフーリエ逆変換も任意の関数です。したがって解は1階微分可能な任意の関数$f(\xi)=f(x-ct)$、$g(\eta)=g(x+ct)$を用いて、

$$u(x,t)=f(\xi)+g(\eta)=f(x-ct)+g(x+ct)$$

と表すことができます。

$k<0$の場合に限定されますが、前章のダランベールの解と一致します。

3.6 境界値問題

次に境界値が与えられた場合の解を求めましょう。

改めて、3.3節と3.4節で求めた解です。

$$X(x) = C_1 \cos (\sqrt {-k} + C_2 \sin (\sqrt {-k} x) $$

$$T(t) = C_3 \cos ( \sqrt{-k}c t) + C_4 \sin (c \sqrt{-k}c t) $$

これに、

$$u(0,t)=u(L,t)=0$$

という境界条件を追加してみます。

$$X(0)=X(L)=0$$

より、$X(x)$の式に$x=0$、$x=L$を代入すると、

$$C_1 = 0$$

$$\sin (\sqrt{-k} L) = 0$$

となります。下の図は$x=0$と$x=L$を通る最も周期が長い三角関数（赤）と周期がその半分の三角関数（橙）を示しています。もちろん、波の大きさは1通りではないし、さらに周期が短い三角関数も含まれます。

最も周期が長い三角関数の位相が$n \pi$のとき（$n$は整数）なので

$$ \sqrt{-k} L = n \pi $$

です。

$$\sqrt{-k} = \frac {\pi}{L} = \omega$$

とすると、1次結合より

$$X(x)= \sum_{n=1}^{\infty} A_{n} \sin (n \omega x)$$

と表すことができます。

$T(t)$はこの境界値によって変わりませんが、$\sqrt{-k}$を置き換え、1次結合により、

$$T(t) = \sum_{n=1}{\infty} \left \{ B_n \cos (nc \omega t) + D_n \sin (nc \omega t) \right \}$$

$u(x,t)=X(x)T(t)$より、

$$u(x,t)= \sum_{n=1}^{\infty} \sin (n \omega x) \left \{ P_n \cos (nc \omega t) + Q_n \sin (nc \omega t) \right \} $$

が得られます。以上、$A_n$、$B_n$、$D_n$、$P_n$、$Q_n$は定数です。

前節で（折りたたんでいますが）、変数分離によって波動方程式の解を求めると（$k<0$の場合）フーリエ変換で表すことができると述べました。これは角周波数の分布が連続的であるともいえます。

境界条件を追加すると、その条件によっては角周波数の分布は離散的になります。つまりフーリエ級数で表すことができるようになります。本節のように2点を通ることを条件とすると、三角関数の半周期が2点の距離と一致する三角関数に限定されるようになります。また、位相も決まります。

3.7 初期値問題

前節で境界条件を追加しましたが、さらに以下の初期条件を加えてみます。

$$ u(x,0)=p(x) \tag { 1 } $$

$$\left . \frac {\partial u(x,t)}{\partial t} \right |_{t=0}=q(x) \tag { 2 } $$

$p(x)$と$q(x)$は任意の関数です。前節の解に$t=0$を代入すると$ (1) $は、

$$u(x,0)= p(x) = \sum_{n=1}^{\infty} P_n\sin (n \omega x) $$

前節の最後の式を$t$について偏微分すると、

\begin{align}
\frac {\partial u(x,t)}{\partial t} = \sum_{n=1}^{\infty} \sin (n \omega x) \left \{ -P_n nc \omega \sin (nc \omega t) + Q_n nc \omega \cos (nc \omega t) \right \}
\end{align}

$t=0$を代入し$ (2) $は以下になります。

\begin{align}
\left. \frac {\partial u(x,t)}{\partial t} \right |_{t=0} = q(x) = \sum_{n=1}^{\infty} Q_n nc \omega \sin (nc \omega x)
\end{align}

これで$p(x)$、$q(x)$が三角関数と定数によって表されました。

逆に$P_n$と$Q_n$を三角関数と$p(x)$、$q(x)$で表すことを考えます。どうすればよいでしょう。

$p(x)$と$q(x)$はフーリエ級数で表されており、$P_n$と$Q_n$はその係数です。係数を取り出すためには同じ周波数・位相の三角関数を掛けて積分してやればよいのでした。よければ「フーリエ変換3」を確認ください。

前節の境界条件で$ u(0,t)=u(L,t)=0 $としました。$x=0$から$x=L$までの区間は解の中で最も長い周期の三角関数の半周期です。したがって積分区間は1周期である$[0,2L]$とします。

$$ P_n = \frac {1} {L} \int_0^{2L} p(x) \sin(n\omega x) dx$$

$$ Q_n = \frac {nc\omega} {L} \int_0^{2L} q(x) \sin(n\omega x) dx$$

これを前節の最後の式に追加すると解が得られます。

\begin{align}
u(x,t) = \sum_{n=1}^{\infty} \sin (n \omega x) & \left \{ \frac {1} {L} \int_0^{2L} p(x) \sin(n\omega x) dx \cos (nc \omega t) \right .\\
& + \left .\frac {nc\omega} {L} \int_0^{2L} q(x) \sin(n\omega x) dx \sin (nc \omega t) \right \}
\end{align}

3.8 境界問題の物理的意味

3.6節で述べたように、変数分離によって波動方程式の解を求めると（$k<0$の場合）フーリエ逆変換で表すことができ、角周波数の分布は連続的でした。

境界条件を追加すると、その条件によっては角周波数の分布は離散的になります。つまりフーリエ級数で表すことができるようになります。3.8節のように2点を通ることを条件とすると、両者の距離が半周期の整数分の一の三角関数に限定されるようになります。また、位相も決まります。

4 まとめ

4.1 概要

・波動方程式は以下の式です。

$$\frac {\partial^2 u} {\partial t^2} = c^2 \frac {\partial ^2 u} {\partial x^2}$$

・一般解は以下です。
$$u(x,t)=f(x-ct)+g(x+ct)$$
$f$と$g$は微分可能かつ1階導関数（1度微分した関数）は連続である任意の関数です。

・一般解からわかるように、$x$を横軸としたグラフ上では2つの関数が左右に速さ$c$で移動します。移動によってそれぞれの波の形は変化しません。

4.2 変数の変換による解法

・$\xi=x-ct$、$\eta=x+ct$として波動方程式を変形すると以下になります。
$$\frac {\partial^2 u}{\partial \xi \partial \eta } = 0$$
この式より$u$は任意の関数$f(\xi)$と$f(\eta)$が解となり、以下のように一般解が得られます。
$$u = f(\xi)+g(\eta) = f(x - ct) + g(x + ct) $$
一般解はダランベールの解ともよばれます。

・以下の初期条件を追加すると、
$$u(x,0)=u_0(x) \quad$$
$$\left . \frac {\partial u(x,t)} {\partial t} \right |_{t=0} = u_1(x) \quad$$
解は以下になります。
$$u(x,t)=\frac {1}{2} \left \{ u_0(x-ct) + u_0(x+ct) \right \} + \frac {1}{2c} \int_{x-ct} ^{x+ct} u_1(y) dy $$
これをダランベールの式とよびます。

4.3 変数分離による解法

・$u$を$x$と$t$の関数の積として表すと、
$$u=X(x)T(t)$$
$x$の方程式と$t$の方程式に分離することができます。
$$\frac {d ^2 X(x)} {d x^2} =kX(x)$$
$$\frac {d^2 T(t)}{d t^2} =kc^2T(t)$$
$k$を分離定数とよびます。
特定の$k$に対して$X(x)$、$T(t)$それぞれの解は指数関数和として表すことができます（$k < 0$の場合）。
その積である$u$も指数関数の和として表すことができます。

・境界条件を追加し、$k$を限定せずに（ただし$k < 0$とします）解を求めると、境界条件によっては解は周期関数の級数で表されます。
これはフーリエ級数と同じです。

1 1次元波動方程式の定義と一般解

1.1 波動とは？

1.2 1次元波動方程式の定義

1.3 移流方程式と物理的意味

1.4 波動方程式の物理的意味

1.5 波動方程式の一般解

2 変数変換による解法（ダランベールの解・式）

2.1 一般解（ダランベールの解）

2.2 初期値問題（ダランベールの式）

2.3 ダランベールの式の物理的意味

2.4 ダランベールの式のグラフ

3 変数分離による解法

3.1 変数分離

3.2 1階微分方程式

3.3 \( \displaystyle \frac {d ^2 X(x)} {d x^2} =kX(x) \)の解

3.4 \(\displaystyle \frac {d^2 T(t)}{d t^2} =kc^2T(t)\)の解

3.5 \(k<0\)の場合の解の物理的意味

3.6 境界値問題

3.7 初期値問題

3.8 境界問題の物理的意味

4 まとめ

4.1 概要

4.2 変数の変換による解法

4.3 変数分離による解法