フーリエ変換3（フーリエ係数の導出）

フーリエ変換2では周期関数を三角関数の和で表すことができると述べました。本ページではそれぞれの項の係数（フーリエ係数）の求め方を説明します。

1 特定の角周波数成分のみを取り出す方法

1.1 どうやって特定の角周波数成分のみを取り出す？

改めて、フーリエ級数の定義です。

$$f(x)= \frac{a_0}{2}+\displaystyle \sum_{k=1}^{\infty}(a_k\cos kx + b_k\sin kx)$$

この中で特定の項の係数（フーリエ係数）を求めます。複数の三角関数が混在している中から特定の項の係数を求めるのですから簡単ではありません。どうしたらよいでしょう。

三角関数を掛けてみましょう。三角関数を掛けると特定の場合のみ違った結果になります。この性質を利用し係数を求めます。以下この手順について述べます。

1.2 掛ける三角関数の角周波数による違い

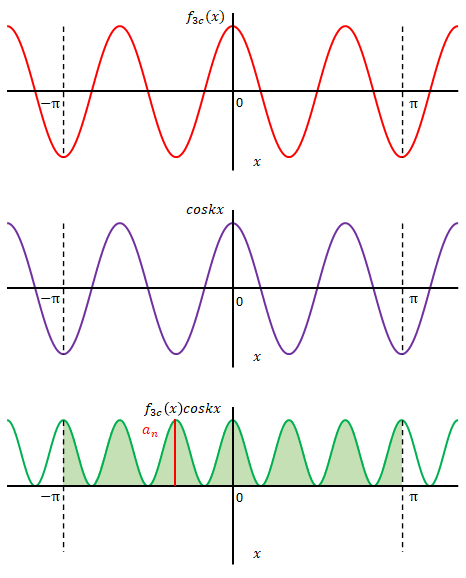
$f_{3c}(x)=\cos 3x$とします。 $f(x)$の一つの項を取り出した関数と思ってください。角周波数は$\cos x$の3倍です。

$f_{3c}(x)$に$\cos 1x$…$\cos 5x$を順に掛けてみます。 $\cos x$ の角周波数の1倍から5倍までです。

それぞれのグラフの意味は以下です。

1段目（赤）：$f_{3c}(x)=\cos 3x$

2段目（紫色）：$\cos x$…$\cos 5x$

3段目（緑色）：$f_{3c}(x)\cos x$…$f_{3c}(x)\cos 5x$（1段目と2段目の関数の積）

※ これまで変換前の関数の変数（$x$）は0以上についてグラフに表示していましたが、下の図ではマイナスから表示しています。

上のグラフの3段目に注目してください。$\cos x$から$\cos 5x$の中で一つだけ、全て縦軸の値が0以上になっている場合があります。1段目の周期と2段目の周期が同じになっている場合ですね。

このときの2段目の関数は$\cos 3x$です。自分自身を掛けているのと同じですから2乗していることになります。したがって3段目の値は必ず0以上になります。

縦に点線を引いてありますが、これは$x$が$-\pi$と$\pi$の位置です。フーリエ級数の定義に関わる位置です。後述します。

$f_{3c}(x)$と同じ角周波数の$\cos$を掛けるとそのグラフ上の面積が0以上になることがわかりました。

1.3 掛ける三角関数の位相（$\cos/\sin$）による違い

前節では対象の関数と掛ける三角関数をどちらも$\cos$としました。次に、対象の関数は$\cos$のまま、掛ける三角関数を$\sin$に変えます。

今度はいずれの場合も面積は0となります。角周波数が同じであっても掛ける関数の位相（$\cos / \sin$）が同じでないと面積は0を超えることはありません。

2 フーリエ係数の導出

2.1 角周波数・位相と面積の関係

前章より、対象の関数と掛ける三角関数の角周波数・位相（$\cos / \sin$）と掛けた後の関数のグラフ上面積を整理すると以下です。

・角周波数と位相（$\cos / \sin$）が一致する場合
　→面積は0以外の値になる
・角周波数は一致しないが位相が一致する場合
　→面積は0になる
・角周波数は一致するが位相が一致しない場合
　→面積は0になる

2.2 $a_n$と$b_n$（$n \gt 0$）の導出

グラフ上の面積より$a_n$と$b_n$を得るにはどうしたらよいでしょう。

下記の通り、$f(x)$は $\cos kx$と$\sin kx$ 級数で表すことができます。

$$f(x)= \frac{a_0}{2}+\displaystyle \sum_{k=1}^{\infty}(a_k\cos kx + b_k\sin kx)$$

この両辺に$\cos nx$、$\sin nx$（$n$は整数）を掛けて面積を求めるとどうなるでしょう。

前述の通り、右辺はある特定の項だけが0以外の値として現れます。下図の例のように、その面積には$a_n$または$b_n$が含まれているはずです。

左辺は$f(x)$を積分した式です。

したがってこれを変形すれば $a_n$と$b_n$を$f(x)$の式で表すことができるはずです。

では面積を求めるにはどうすればよいでしょう。

積分ですね。

その結果が以下です。

$$a_n = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \cos nx dx$$

$$b_n = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \sin nx dx$$

ただし、$a_0$の式は次項で求めます。

導出の過程を表示する場合は「＋」のところを押して展開してください。

フーリエ係数の導出1

$f(x)$に$\cos nx$を掛けて$-\pi$から$\pi$の区間で積分します。
\begin{align*}
\int_{-\pi}^{\pi} f(x) \cos nx dx &= \int_{-\pi}^{\pi} \{ \frac{a_0}{2}+\displaystyle \sum_{k=1}^{\infty}(a_k\cos kx + b_k\sin kx) \} \cos nx dx \\
\end{align*}
前述の通り、角周波数または初期位相（$\sin $ または $\cos $）が異なる2種類の三角関数の積を積分しても0になるので、それらの項を消去します。
\begin{align*}
\int_{-\pi}^{\pi} f(x) \cos nx dx &= \int_{-\pi}^{\pi} (\frac{a_0}{2}+a_n\cos nx) \cos nx dx \\
\end{align*}
$\frac{a_0}{2} \cos nx$を$-\pi$から$\pi$まで積分するということは$n$周期の積分なのでこれも$0$になります。
\begin{align*}
\int_{-\pi}^{\pi} f(x) \cos nx dx &= \int_{-\pi}^{\pi} a_n\cos nx \cos nx dx \\
&= a_n \pi
\end{align*}
\begin{align*}
a_n &= \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \cos nx dx
\end{align*}
b_nの求め方も同様です。掛ける関数を$\cos nx$から$\sin nx$に変えるだけです。
\begin{align*}
\int_{-\pi}^{\pi} f(x) \sin nx dx &= b_n \pi \\
\end{align*}
\begin{align*}
b_n &= \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \sin nx dx
\end{align*}
以上、$a_n$と$b_n$を求める式が得られました。

2.3 $a_0$の導出

フーリエ級数には$\dfrac{a_0}{2}$という定数の項があります。$a_n$や$b_n$とは性質が違うように思われますが、導出の過程は同じです。

前項の$a_n$や$b_n$の求める際、三角関数を掛け積分の式にしました。

$a_0$も同じように求められます。$\cos 0x=1$を掛ければよいのです。その結果が次の式です。

$$a_0 = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) dx $$

$\dfrac{b_0}{2}$を求めようとすると$\sin 0x=0$を掛けることになります。これを他の項と同じ定義で求めると$b_0=0$になります。フーリエ級数に$b_0$の項が存在しないのは、定数の項が2種類も必要ないということもありますが、そもそも他の項と同じ定義に従うと0になるからです。

下の「＋」を押すと導出の過程を表示します。

フーリエ係数の導出2

前述と同様に$\cos$、$\sin$を掛けて積分します。
$\cos kx $と$sin kx $を$\pi$から$-\pi$までで積分すると0になるので途中でそれらの項を削除しています。
\begin{align*}
\int_{-\pi}^{\pi} f(x) \cos 0x dx & = \int_{-\pi}^{\pi} f(x) dx\\
& = \int_{-\pi}^{\pi} \{ \frac{a_0}{2}+\displaystyle \sum_{k=1}^{\infty}(a_k\cos kx + b_k\sin kx) \} dx \\
& = \int_{-\pi}^{\pi} \frac{a_0}{2} dx \\
& = 2 \pi \cdot \frac{a_0}{2} \\
& = a_0 \pi \\
\end{align*}
\begin{align*}
a_0 &= \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) dx \\
\end{align*}

ところで、なぜフーリエ級数の定数の項は$a_0$ではなく$\dfrac{a_0}{2} $で定義されているのでしょう。
前述の定義を見比べてみればわかりますが、フーリエ級数の定数の項を$\dfrac{a_0}{2} $ではなく$a_0$とすると$a_0$だけ$\dfrac{1}{2} $になります。
導出の過程で以下の違いがあるからです。
\begin{align*}
\int_{-\pi}^{\pi} \cos nx \cos nx dx &= \pi \quad \text{(1)} \\
\end{align*}

\begin{align*}
\int_{-\pi}^{\pi} \sin nx \sin nx dx &= \pi \quad \text{(2)} \\
\end{align*}

\begin{align*}
\int_{-\pi}^{\pi} \cos 0x \cos 0x dx &= 2\pi \quad \text{(3)} \\
\end{align*}

$\cos$の後が0の場合に限り2倍になっています。ではなぜ2倍になるのでしょう。
$b_0$がなぜ不要かを思い出してください。
$\cos$では2倍になるが、$\sin$では0になるのです。

\begin{align*}
\int_{-\pi}^{\pi} \sin 0x \sin 0x dx &= 0 \quad \text{(4)} \\
\end{align*}

$a_n+b_n$、$a_0+b_0$はいずれも$2\pi$となり、この点で違いはありません。角周波数が0の場合は$a$の項に偏ったと考えてください。詳細の説明は長くなるため、なぜ偏るかについては省略します。

3 まとめと補足

3.1 フーリエ係数の式

フーリエ係数を求める式は以下です。

$$a_n = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \cos nx dx$$

$$b_n = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \sin nx dx$$

$$a_0 = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) dx $$

3.2 その他

・$\cos$に$\cos$、$\sin$に$\sin$を掛けて周期の整数倍の範囲で面積を求めると（積分すると）、角周波数が同じ場合のみ0以上の値になります。角周波数が異なる場合は0になります。

・掛けられる関数と掛ける関数の角周波数が異なっている場合や$\cos$に$\sin$または$\sin$に$\cos$を掛ける場合は積分した値は0になります。

・上記の性質を利用して$f(x)$に$\cos$または$\sin$を掛けて$-\pi$から$\pi$まで積分することにより特定の項のフーリエ級数を求めることができます。

3.3 補足：本ページで触れていない説明

係数を求めるために$f(x)$に$sin$または$cos$を掛けて積分する際、範囲を$-\pi$から$\pi$にしました。これは$f(x)$の1周期分を$2\pi$としていたからです。周期がそれ以外であれば上記式の通りにはなりません。周期を$T$とすると以下の式になります。

$$a_n = \frac {2} {T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \cos \frac{2\pi nx}{T} dx$$

$$b_n = \frac {2} {T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \sin \frac{2\pi nx}{T} dx$$

$$a_0 = \frac {2} {T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) dx $$

本ページは$T=2\pi$とした場合の説明でした。