フーリエ変換2、フーリエ変換3ではフーリエ級数について述べました。フーリエ級数についてはこれで終わりかというとそうではありません。ここまでは係数も三角関数の変数も実数でした。しかしこの係数を複素数で表すことができます。これを複素フーリエ級数とよびます。区別するために実数で表すフーリエ級数を実フーリエ級数とよぶこともあります。
実フーリエ級数から複素フーリへ級数を導出する手順を考えましょう。
1 補足
1.1 複素平面
複素数を扱う演算をイメージするために複素平面(複素数平面)がよく使われます。複素平面上での演算について確認しておきましょう。
通常、横軸を実部、縦軸を虚部として表します。
足し算は2次元のベクトルと同じように求めることができます。
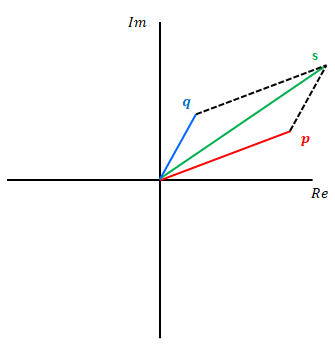
引き算も同様です。
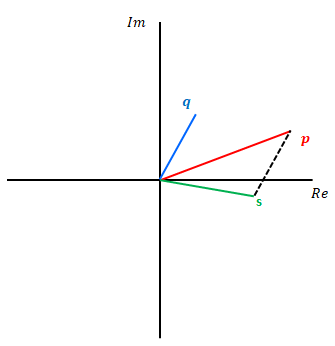
複素数の掛け算はベクトルの内積や外積とは異なります。下の図の緑色は複素平面において赤色と青色を掛けた値です。
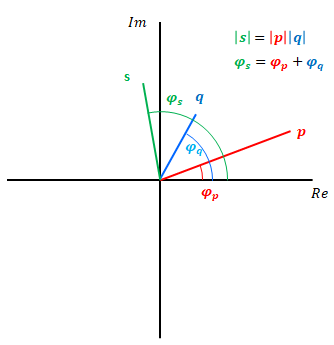
掛け算の規則は以下です。絶対値と偏角に分けて考えます。
絶対値:実部の2乗と虚部の2乗の和の平方根です。複素平面上では原点からの長さです。掛ける数と掛けられる数の絶対値の積により求まります。
偏角:複素平面上の点と原点を結んだ線と実軸(実部の軸)がなす角です。掛ける数と掛けられる数の偏角の合計により求まります。
2 フーリエ係数の導出
2.1 \(c_k\)と\(c_{-k}\)を\(a_k\)と\(b_k\)の式で定義する
さて、複素フーリエ級数についてです。
改めて、実フーリエ級数の定義です。
$$f(x)= \frac{a_0}{2}+\displaystyle \sum_{k=1}^{\infty}(a_k\cos kx + b_k\sin kx)$$
$$a_n = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \cos nx dx$$
$$b_n = \frac {1} {\pi} \int_{-\pi}^{\pi} f(x) \sin nx dx$$
フーリエ係数は全て実数です。この係数を複素数に変えるところから始めます。
係数\(c_k\)を以下のように\(a_k\)と\(b_k\)の式で定義します。
$$c_k=\frac{a_k – ib_k}{2} $$
$$c_{-k}=\frac{a_{k} + ib_{k}}{2} $$
$$c_0=\frac{a_0}{2} $$
これ以外に複素数で表すことができないわけではありませんが、この関係にしておくと複素フーリエ級数が都合の良い形になります。
なお、本ページでは添え字に\(n\)を使っているところと\(k\)を使っているところがあります。大きな違いはありませんが、\(k\)は正の整数、\(n\)は全ての整数として区別しています。\(-k\)は、負のときの\(n\)に相当します。
\(a_k\)、 \(b_k\)と\(c_k\) 、\(c_{-k}\)は複素平面上ではどのような関係にあるでしょう。
上の式を変形します。1番目の式と2番目の式を足すと\(a_k\)、2番目の式より1番目の式を式を引くと\(b_k\)になります。
$$a_k=c_{-k}+c_{k}$$
$$b_k=c_{-k}-c_{k}$$
下の図の左側の赤色が\(c_k\)、青色が\(c_{-k}\)です。\(a_k\)は実軸、\(b_k\)は虚軸上にあります。補助線を追加したのが右の図です。上の式の関係の通りであることがわかります。
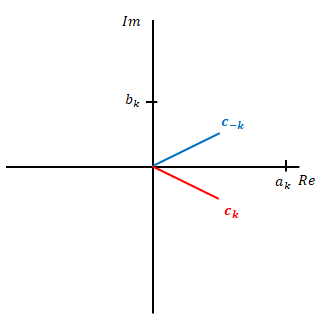
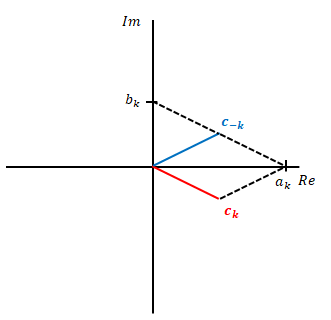
\(c_k\)と\(c_{-k}\)複素共役の関係にあります。複素共役とは、実部の値が同じ、虚部の値は絶対値が同じで符号が反対の関係のことです。
2.2 オイラーの公式
変わるのは係数だけではありません。実フーリエ級数における三角関数を指数関数に置き換えます。
ここで必要になるのが「オイラーの公式」です。以下の関係にあります。
$$e^{i\theta}=\cos \theta+i\sin \theta$$
\(e\)はネイピア数(2.718…)、\(i\)は虚数単位です。
\(e\)の指数部が虚数となっています。実数であればその値が無限大において発散するか0に収束するのですが、虚数であればオイラーの公式に従い三角関数の和になるので絶対値は振動します。
\(e^{i \theta}\)は複素平面上ではどう表されるでしょう。オイラーの公式から、その実部は\(\cos \theta \)、虚部は\(\sin \theta \)です。実軸・虚軸上のこれらの値からの垂線の交点が複素平面上の\(e^{i \theta}\)です。
\(e^{i \theta}\)の絶対値は複素平面上では原点からの距離です。以下の式より常に1であることがわかります。
$$| e^{i \theta}|=\sqrt{\cos^2 \theta +\sin^2 \theta } =1$$

\(\theta\)を0から大きくしていくと\(e^{i \theta}\)は図のように円周上を移動します。円弧の部分が\(\theta\)です。

2.3 \(f(x)\)を\(c_{}\)の式で表す
このオイラーの公式をフーリエ級数に適用し\(a_k\)、 \(b_k\)、 \(\sin\) 、\(\cos\)を新たに定義した\(c_n\)と\(e\)で置き換えます。その結果が下の式です。
$$f(x)= \displaystyle \sum_{n=-\infty}^{\infty} c_n e^{inx}$$
詳細は下の「+」を押して展開してください。
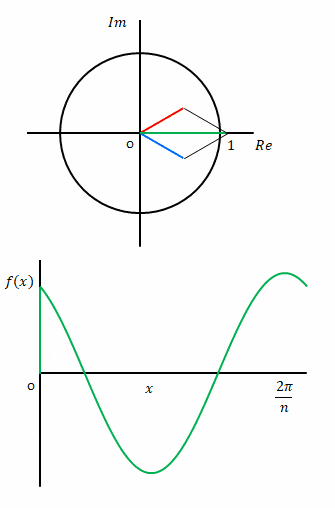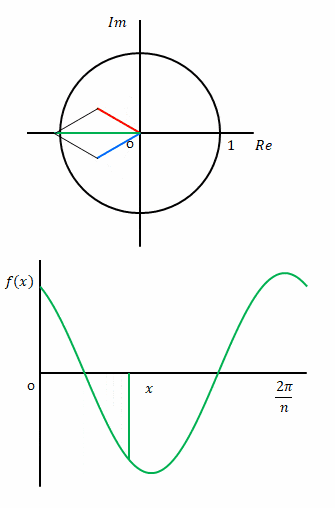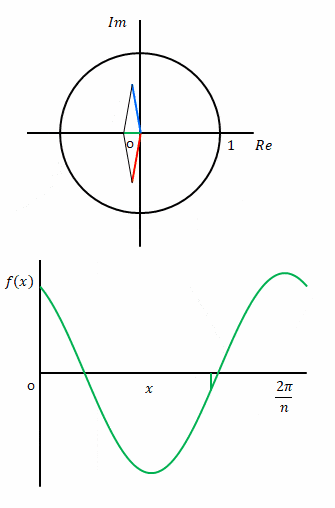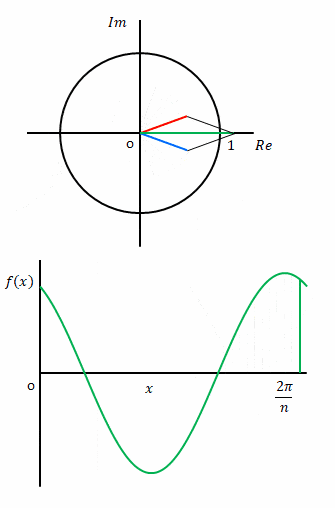
この\(f(x)\)を複素平面で表すとどうなるでしょう。
下の図は\(x\)を増やしながら複素平面上で変化していく様子を表しています。
左側の図はパンタグラフのようなものが左右に動いているようにみえますが、そうではありません。\(c_k e^{-ikx}\)(青色)と\(c_{-k} e^{ikx}\)(赤色)が円周上を動いているところを合わせて描いています。さらに実軸上の緑色は両者の和、つまり
$$c_k e^{-ikx} +c_{-k} e^{ikx}$$
を示しています。
右側の図はこれに合わせて\(f(x)\)を表示しています。
2.4 \(c_{n}\)を\(f(x)\)の式で表す
次は逆に\(c_{n}\)を\(f(x)\)の式で表します。
2.1節では\(c_k\)と\(c_{-k}\)を定義しました。しかしこれは\(a_k\)と\(b_k\)の式として表したものです。複素フーリエ級数を表現することはできるのですが、あえて\(a_k\)と\(b_k\)を使う必要はありません。直接\(f(x)\)を\(c_n\)で表すことができます。
2.1節の定義の式の\(a_k\)と\(b_k\)に\(f(x)\)の式を入れると以下になります。
$$ c_n = \frac {1} {2\pi} \int_{-\pi}^{\pi} f(x) e^{-inx} dx$$
詳細は下の「+」を押して展開してください。
2.5 なぜ\(f(x)\)に\(e^{-inx}\)を掛けて\(-\pi\)から\(\pi\)で積分する?1
複素平面上の定義では、\(f(x)\)に\(e^{-inx}\)を掛けて\(-\pi\)から\(\pi\)で積分しています。これはどのような意味があるのかを複素平面上でみてみましょう。
以下の関数を例とします。\(c_{-k}\)と\(c_{k}\)以外の係数は0とします。
$$f(x)=c_{-k}e^{-ikx}+c_{k}e^{ikx}$$
係数は\(c_{-k}\)と\(c_{k}\) 以外は存在しませんが、あえて\(k\)とは別の整数\(m\)によって\(c_m\)を表したとします。\(m\)も\(k\)も正とします。\(m\)と\(k\)は異なる値であれば、\(c_m\)は0となるはずです。このことを確認します。
$$ c_m = \frac {1} {2\pi} \int_{-\pi}^{\pi} f(x) e^{-imx} dx$$
この積分の中を展開します。
$$f(x) e^{-imx} = c_{-k}e^{-ikx} e^{-imx} + c_{k}e^{ikx} e^{-imx} $$
左と右の項を以下のように定義します。
$$g_{left}(x) = c_{-k}e^{-ikx} e^{-imx}$$
$$g_{right}(x) = c_{k}e^{ikx} e^{-imx}$$
以下、左の項と右の項に分け、さらに右の項は\(m\)と\(k\)が同じ値の場合と異なる値の場合に分け、計3通りについて 考えます。
2.5.1 \(g_{right}\)(\(m \neq k\))
下の図は\(x\)を増やしながら3種類の値を表示しています。
オレンジ色は\(c_{k}e^{ikx}\)です。指数部が正なので\(x\)が増えるとともに反時計回りに動いています。
紫色は\(e^{-imx}\)です。指数部が負なので時計回りです。
緑色はオレンジ色と紫色を掛けた値、つまり \(g_{right}(x)\)です。 回転の方向と速度は \(c_{k}e^{ikx}\) と \(e^{-imx}\) によって決まります。ただし、\(m \neq k\)なので必ずどちらかの方向へ回転します。

2.5.2 \(g_{left}\)(\(m=k\))
オレンジ色と紫色は同じ大きさの速度で向きは逆です。したがって \(g_{right}(x)\) は静止します。

2.5.3 \(g_{left}\)(\(m\)と\(k\)の関係に関わらず)
\(m\)も\(k\)も正と定義していたため、下図のように必ず\(g_{left}\)は反時計回りに回転します。

2.6 なぜ\(f(x)\)に\(e^{-inx}\)を掛けて\(-\pi\)から\(\pi\)で積分する?2
緑色の棒が回転する場合と回転しない場合がありますが、この違いは何に関わってくるのでしょう。
オレンジ色と紫色の角周波数は整数です。その積である緑色の 角周波数も整数です。\(\pi\)から\(\pi\)の間に整数回だけ回転します 。
したがって\(m \neq k\)のときは\(\pi\)から\(\pi\)の区間で積分をすると必ず0になります。
\(m = k\)のときの緑色の角周波数も整数ですが0です。静止しました。 \(\pi\)から\(\pi\) の区間で積分をすると\(2\pi\)倍になります。積分の外の \(2\pi\) と相殺され\(c_m=c_k\)が残ります。
結局 \(m = k\) のときに\(c_m = c_k\)、 \(m \neq k\) のときに\(c_m = 0\)であるという、当たり前の結論を証明しただけですが、以下が確認できました。
・\(f(x)\)の\(e^{ikx}\)の成分に掛ける指数関数が角周波数の大きさが同じで逆に回転する場合
積は固定値。これを積分し\(2\pi\)で割ると\(c_k\)になる。
・上記以外
積は回転する。積分すると0。
式で確認するには「+」を押して展開してください。
2.7 複素フーリエ級数の値は複素数?
\(f(x)\)は実数であったとします。複素フーリエ級数に展開し、展開した後の各項を足すと複素数でしょうか。
実数ですね。展開する前と後で\(f(x)\)の値が変わるわけではありません。係数は特殊な場合を除き複素数です。\(e\)の指数部は虚数です。しかし和を求めると虚部は打ち消しあいます。
下は2.3節と同じ図です。赤色は\(c_k e^{ikx}\)、青色は\(c_{-k} e^{-ikx}\)、緑色は\(f(x)\)です。

\(c_{k}\)と\(c_{-k}\)は複素共役でしたね。\(c_{k} e^{-ikx}\)と\(c_{-k} e^{ikx}\)も複素共役です。複素共役の数の和である\(f(x)\)は実数になります。
実数の関数を複素フーリエ級数に展開しても、関数の値が複素数に変わるわけではありません。級数の中に複素数が存在しますが、虚数は打ち消しあいます。
では\(f(x)\)が複素数だった場合はどうでしょう。そもそも展開できるのでしょうか。ここでは詳細を述べませんが、展開は可能です。その場合はもちろん展開した後の項の和は複素数です。
3 まとめ
3.1 定義
複素フーリエ級数の定義は以下です。
$$f(x)= \displaystyle \sum_{n=-\infty}^{\infty} c_n e^{inx}$$
$$ c_n = \frac {1} {2\pi} \int_{-\pi}^{\pi} f(x) e^{-inx} dx$$
3.2 その他
・本ページで実フーリエ級数から複素フーリエ級数を求めた手順は以下でした。
①\(c_k\)と\(c_k\)を\(a_k\)と\(b_k\)の式で定義する。
②\(f(x)\)を\(c_n\)の式で表す。
③\(c_n\)を\(f(x)\)の式で表す。
・\(c_n\)を求める際、\(f(x)\)に\(e^{-inx}\)を掛けて\(-\pi\)から\(\pi\)で積分します。これは、もし\(f(x)\)に\(e^{inx}\)が含まれていたら、その係数が積分値となって現れるという性質を利用しているからです。
・複素フーリエ級数は複素数を使って関数を表現しますが、級数の値が複素数になるわけではありません。演算の途中で虚数が現れますが、結果は実数です。複素数を使うと都合がよいからこのようにしているだけです。
3.3 補足:なぜ複素数を使う?
フーリエ級数は実数の係数と三角関数だけで表現できます。しかしあえて複素数と指数関数で表すよう変更しました。なぜ複素数を使うのでしょう。
一つは級数が簡単になるからでしょう。実フーリエ級数では\(cos\)、\(sin\)、定数の項がありました。しかし複素フーリエ級数では\(e\)の項しかありません。実際には\(n\)が負の項もあるので数としては変わらないのですが、サメーションを使えば簡単になります。
もう一つは、三角関数を使わなくてよいことだと思います。三角関数のほうがなじみがあるかもしれません。しかし掛け算をすると\(cos\)と\(sin\)が変わります。微分をした場合もそうです。高校の数学を思い出してください。三角関数の演算はややこしかったですね。
しかし指数関数と複素数の組み合わせの場合は掛け算をしても絶対値の積と偏角の和を求めるだけです。指数関数が別のものに変わるわけではありません。
