ここではフーリエ級数を説明します。級数とは複数の項の和によって表される数式のことです。
「フーリエ変換1」 でも述べましたが、フーリエ変換はフーリエ級数と似ているところがあります。フーリエ級数を発展させた形がフーリエ変換とも考えられます。そこで、まずはフーリエ級数について説明します。
1 関数の分解
「フーリエ変換1」で関数を三角関数に分解できることを説明しました。この分解した三角関数の和で表した式が「フーリエ級数」です。本章ではまず初期位相が0の場合に限定してどう分解されるかを考えます(1.1節)。その後で初期位相を限定しない(0以外を含む)場合に広げます(1.2節)。1.1節は説明のための特殊な場合だと理解ください。
「初期位相」とは、これは変数が0のときの位相です。
1.1 初期位相が0の場合
下の図の赤の関数を三角関数に分解し、それぞれがどのような式で表されるかを考えましょう。最後にそれらの和として赤の関数の式を求めます。
下の図のオレンジのグラフが分解した三角関数です。
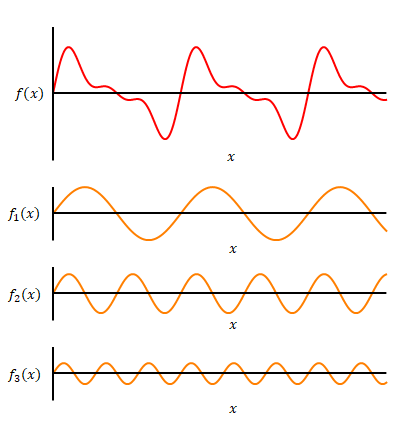
一つ一つ数式にしてみましょう。
これは
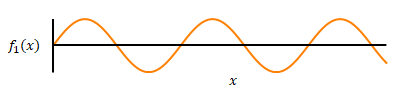
$$f_1(x)=b_1\sin x$$
です。\(b_1\)は定数です。以下\(b_2\)、\(b_3\)も同様です。
\(b_1\)は振幅(大きさ)を示す定数です。三角関数の周期は\(2\pi\)としています(周期がこれ以外の場合は\(x\)に係数がつきます)。
次のグラフは角周波数が2倍なので

$$f_2(x)=b_2\sin 2x$$
です。
角周波数が3倍の場合、

$$f_3(x)=b_3\sin 3x$$
です。
これらを和にした関数、つまり下のグラフを
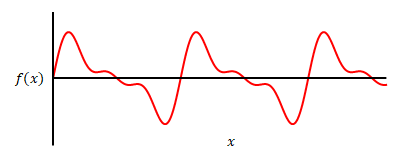
数式にすると以下になります。
$$f(x)=b_1\sin x + b_2\sin 2 x + b_3\sin 3 x$$
これがフーリエ級数の一例です。ただし説明のための特殊な場合です。一般的な定義は次節の通りです。
1.2 初期位相を限定しない場合
以下の波形になる関数は
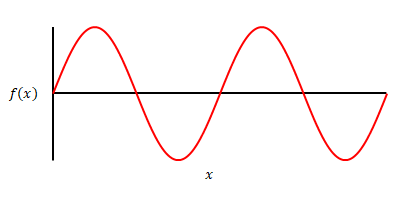
$$f(x)=b\sin x$$
でしたね。
ではこの関数はどうでしょう。同じ角周波数ですがタイミングがずれています(初期位相が異なっています)。
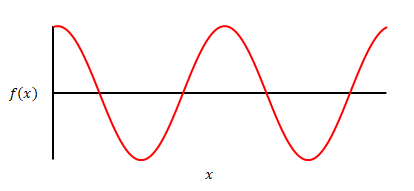
\(\sin\)では表せませんね。\(\cos\)を使う必要があります。
$$f(x)=a\cos x$$
では次のような場合はどうでしょう。
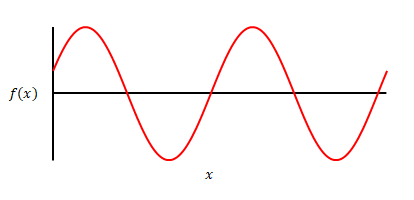
\(\sin\)と\(\cos\)どちらかだけでは表すことができませんが、両者(下図オレンジの関数)の足し算で表すことができます。
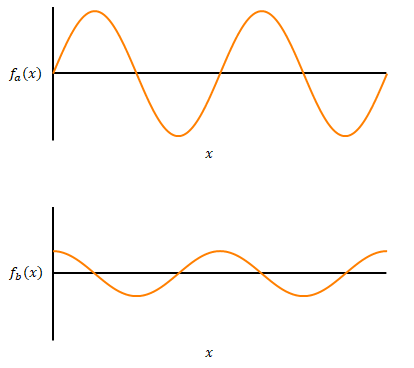
三角関数(赤)の初期位相を変えながらそれを構成する\(\sin\)と\(\cos\)の関係を表したのが下の図です。
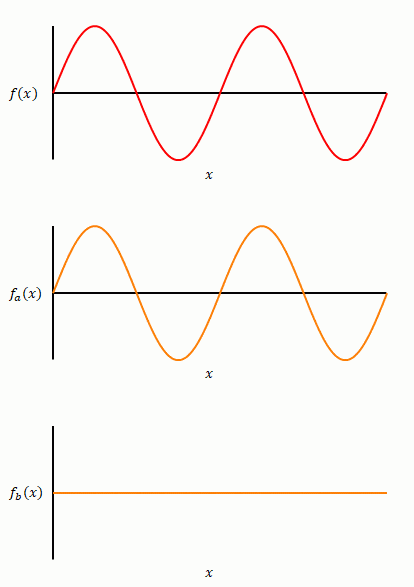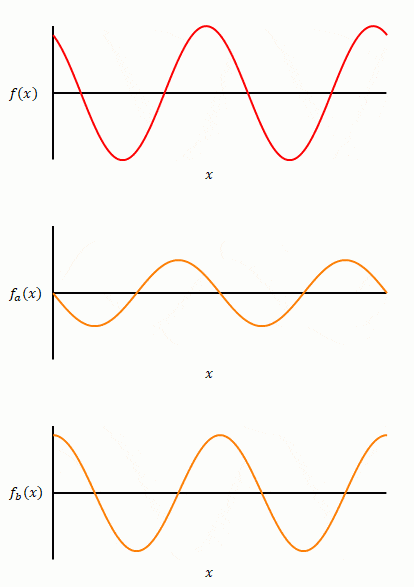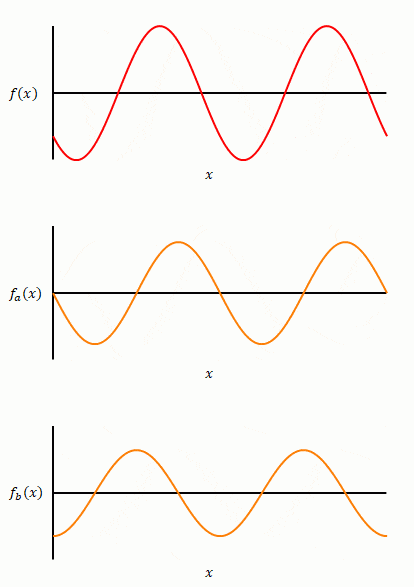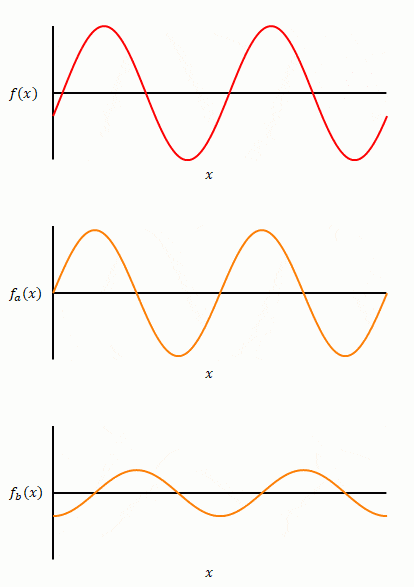
前項ではフーリエ級数を\(\sin\)のみの和で表しましたが、初期位相が0でない三角波を含む場合は\(\cos\)の項が必要になります。
例えばこの関数の場合、
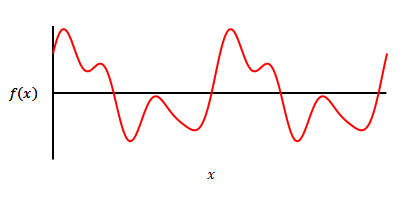
以下のように表すことができます。
$$ f(x) = a_1\cos x + a_3\cos 3x + b_1\sin x + b_2\sin 2x + b_4\sin 4x $$
2 フーリエ級数とは
2.1 フーリエ級数の定義
1.2節では\(\sin\)と\(\cos\)の項の和によってどのような初期位相の関数でも表せることを示しました。
これを一般化するとフーリエ級数の定義になります。
\begin{align*} f(x) =\frac{a_0}{2} & +a_1\cos x +a_2\cos 2x+…+ a_n\cos nx+…\\& +b_1\sin x + b_2\sin 2x +…+ b_n\sin nx+…\end{align*}
\(a_0, a_1, \cdots, b_1, b_2, \cdots\)は定数です。
サメーションを使いこのように表すことができます。
$$f(x)= \frac{a_0}{2}+\displaystyle \sum_{k=1}^{\infty}(a_k\cos kx + b_k\sin kx)$$
\(\displaystyle \frac{a_0}{2}\)は角周波数が0の成分です。つまり\(f(x)\)の平均値と同じ値です。
関数をフーリエ級数で表すことをフーリエ級数展開とよびます。
※ 不連続な関数をフーリエ級数展開すると、不連続なところで値が一致しない場合があるため、「\(=\)」ではなく「\(\sim\)」を使用する場合があります。
2.2 フーリエ級数とフーリエ変換の違い
フーリエ級数とフーリエ変換は、言葉は似ていますが明確な違いがあります。
フーリエ変換は関数を角周波数(または周波数)の関数に変換することです。
フーリエ級数は関数を三角関数の級数で表すことです。
2.3 一定の周期で繰り返す関数とそうでない関数の違い
次のグラフは正規分布です。
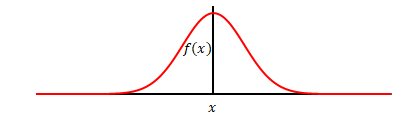
これをフーリエ変換すると次のようになります(角周波数領域でも正規分布になるのですが、ここでは角周波数は0以上を対象として表しています)。
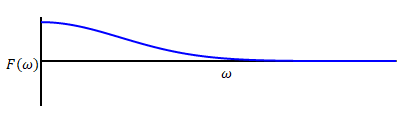
これまで説明で参照した関数とは何かが違いますが何でしょう。
これまでは一定の周期で繰り返す関数が対象でした。それに対し、上の赤の関数は一定の周期で繰り返していません。
前者を周期関数、後者を非周期関数とよぶことにします。
周期関数の場合、その整数倍の角周波数の三角関数に分解することができます。。例えば角周波数が10の関数を分解すると角周波数が10、20、30…のが現れます。角周波数11の三角関数は存在しません。もし10と11の三角関数が存在する場合は元の関数の周期は1になるはずです。10と11の最大公約数が1だからです。
これに対し非周期関数を変換すると角周波数が連続して現れます。関数を三角関数に分解できることに変わりはありませんが、その角周波数は無限に存在し\(F(\omega)\)は連続した値をもつようになります。
後者のように角周波数が連続すると級数で表すことができません。したがってフーリエ級数展開できるのは周期関数のみです。
3 まとめ
・関数を三角関数の項の和で表した式がフーリエ級数です。
・フーリエ級数の定義は以下です。
$$f(x)= \frac{a_0}{ 2}+\displaystyle \sum_{k=1}^{\infty}(a_k\cos kx + b_k\sin kx)$$
・対象の関数が初期位相が0の三角関数で構成される場合は\(sin\)だけで表すことができますが、初期位相が0以外の三角関数を含む場合は級数の\(\sin\)と\(\cos\)の2種類の三角関数の項が必要です。
・周期関数はフーリエ級数で表すことができますが非周期関数はフーリエ級数で表すことはできません。
