フーリエ変換をご存じでしょうか。大学の理工系の学部であれば大半は必修とされているのですが、それ以外の方は初耳かもしれません。
大学で学ぶものなので当然簡単ではありません。しかし概要は理解することができると思います。ここでは最小限の範囲にとどめ、フーリエ変換とはどのようなものかを説明します。
本ページでは、本題に入る前の予備知識について述べます。
1 概要
1.1 フーリエ変換とフーリエ級数
多くの教科書ではフーリエ変換の説明の前にフーリエ級数に説明に多くのページを割いていることと思います。両者は共通の部分が多く、フーリエ級数を発展させた形をフーリエ変換であるとすると理解しやすいからでしょう。
本ページも題名を「フーリエ変換」としましたが、次ページ以降フーリエ級数を説明し、その後でフーリエ変換を説明します。
1.2 基本となる関数
フーリエ級数展開とは対象の関数を周波数ごとに項を分けた級数に展開する演算です。フーリエ変換とは対象の関数を周波数の関数に変換する演算です。
いずれも対象の関数に含まれる周波数成分を抽出する演算ですが、これらの周波数とは三角関数のそれを指します。つまりグラフにすると正弦波(または余弦派)のことです。三角波や矩形波であっても周波数を定義することができますが、単に「周波数」と書かれていれば、それは三角関数であると考えてください。
2 周波数・位相他
本章では周波数、角周波数、周期などの意味について簡単に説明します。これらの言葉は物理学や工学で頻繁に用いられます。時間の進行とともに繰り返し変化する現象が多いからでしょう。
しかしフーリエ変換は純粋な数学であって、時間を変数とした関数だけに限定していません。例えば変位が変数であってもかまいません。したがって周波数などは本来フーリエ変換の説明に使われる言葉ではありません。
しかし、ここではなるべく平易な表現にするためにこれらの言葉を使います。
2.1 周波数
周波数とは変数が1増えるごとに進む周期の数です。周期の逆数で表すことができます。例えば周期を\(x_0\)とすると周波数は\(u_0=\displaystyle \frac{1}{x_0}\)です。波が密になるほど周波数は大きくなり、疎になるほど周波数は小さくなります。
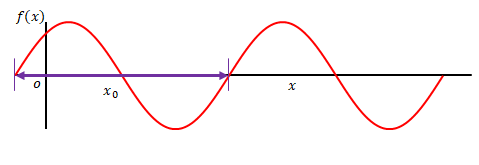
2.2 位相
位相とは、一定の周期で繰り返す関数の括弧の中の値のことで、通常、角度で表します。角度とは、周期を\(2\pi\)とした相対的な値です。
例えば関数が\(f(x)=sin(2\pi u_0 x+\alpha)\)で表される場合、位相は\( 2\pi u_0 x+\alpha \)です。
\(x=x_1\)における位相は\( 2 \pi u_0 x_1+\alpha \)です。

位相差は、周波数が同じ2つの関数の時間差を角度で表したものです。単に位相とよぶ場合もあります。
下図において点線の関数を基準とした実線の関数の位相差は \(2 \pi u_0 x_2\)です。実線のほうが進んでいる点に注意ください。

2.3 角周波数
1.1節では周波数について述べましたが、似た物理量に「角周波数」があります。フーリエ変換ではどちらでも記述は可能ですが、一方を選ばないといけません。周波数で記述した場合と角周波数で記述した場合で係数などに違いが生じます。
フーリエ変換について書かれた書籍やWebサイトは数多く存在しますが、統一されているわけではありません。ややこしい話ですが、周波数と角周波数の違いを理解しましょう。
角周波数は変数が1増えることにより進む角度(次節)のことです。
以下のような関数を例に考えてみます。
$$f(x)=\sin x$$
グラフにすると図のようになります。
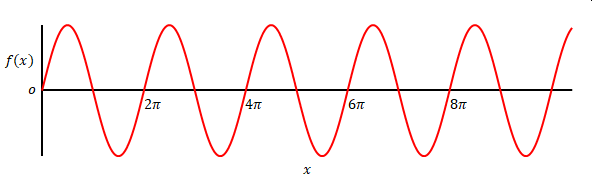
・周波数
上の例では\(x\)が\(2\pi\)増えると周期が1増えているので、周波数は\(\displaystyle \frac{1}{2\pi} \)です。
・角周波数
上の例では\(x\)が\(2\pi\)増えるごとに角度が\(2\pi\)増えているので角周波数は1です(下記)。
$$\frac{2\pi}{2\pi} = 1 $$
・周波数と角周波数の関係
\(x\)が増えて\(f(x)\)が1周期進むと角度は必ず\(2\pi\)進みます。したがって、以下の関係があります。
$$2\pi u=\omega$$
ただし周波数を\(u\)、角周波数を\(\omega\)としています。
この関係は上記の例(\(f(x)=\sin x\))に限らず、一定の周期で変動する関数では常に成立します。
本サイトでは主に角周波数で記述します。
2.4 角度
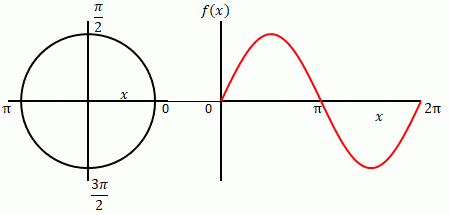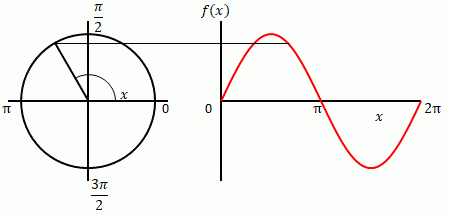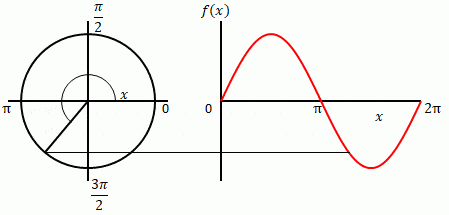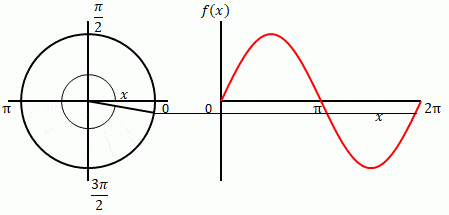
角度とは波の1周期を\(2\pi\)とした相対的な値です。下の左の図のように円を描くと、波の1周期は1回転\(2\pi = 360度\)に相当します。
下の右の図は\(\sin x\)を\(x\)軸と\(y\)軸のグラフにしています。
下の左の図では\(x\)は円の半径と水平方向(右向き)がなす角(扇の部分)です。右の図では横軸が\(x\)です。どちらの図(グラフ)も縦方向が\(\sin x\)です。\(x\)を変えながら左と右の\(\sin x\)を細い線でつないでいます。水平になっていることから両者が一致することを示しています。
\(f(x)=\sin x\)の場合、\(x\)が角度です。角度は\(rad\)で表します。1周すると\(2\pi [rad]\)です(以下\(rad\)を省略します)。
3 重ね合わせの原理
重ね合わせの原理によって複雑な関数のフーリエ変換を単純な関数に分解して考えることができます。非常に重要な原理なのでフーリエ変換を学ぶ前に必ず理解しておきましょう。
3.1 一定の周期で繰り返す関数は三角関数の和で表すことができる?
三角関数ではない、一定の周期で繰り返す関数は三角関数に分解することができます。逆に言えば、複数の三角関数を組み合わせることで(特殊な場合を除き)任意の関数を合成することができます。
3種類の例を用いて説明します。
下の図の赤色は変換前の関数です。3種類の正弦波が合成されています。それらの波がオレンジ色のグラフです。赤色の波からオレンジ色の正弦波を分離させてみたところをイメージしています。
そしてそれぞれの正弦波の周波数ごとに大きさを示したのが青色のグラフです。これが変換後の関数のグラフです。

以下は例として各周波数の成分をリアルタイムに変化させて周波数領域でどう変わるかを表示しています。
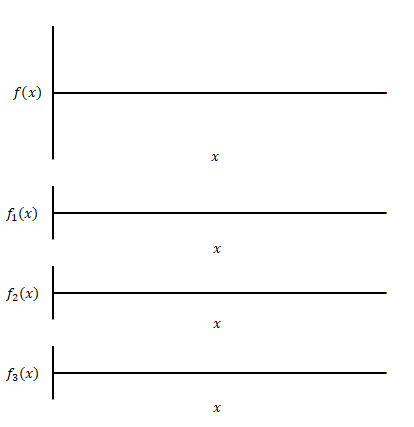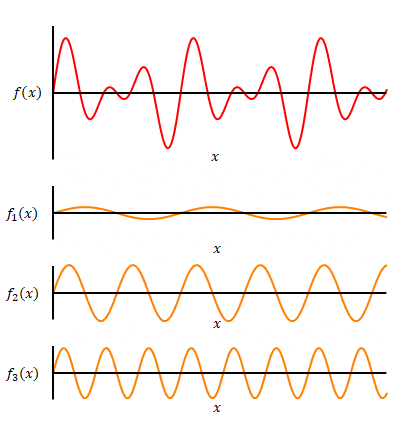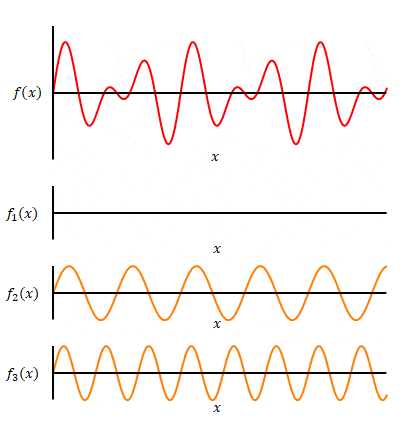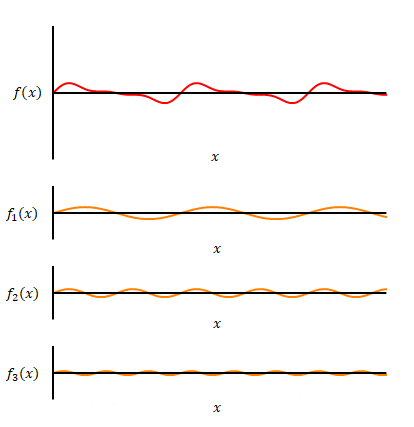
次の図は逆に正弦波を合成する過程です。角が取れた台形状の波を生成している様子です。
※ この例では最も低い周波数の7倍までの正弦波によって誤差がほとんどなく合成していますが、矩形波や三角波のように滑らかでない部分がある波形の場合は高い周波数まで重ね合わせても正確に一致しない場合があります(ギブスの現象またはギブズの現象)。
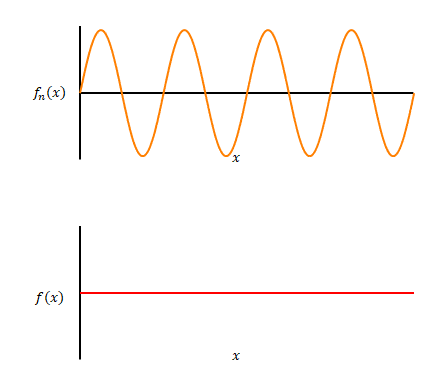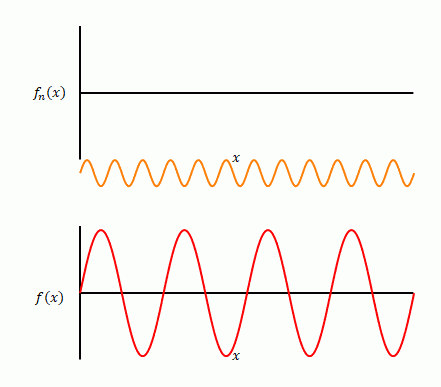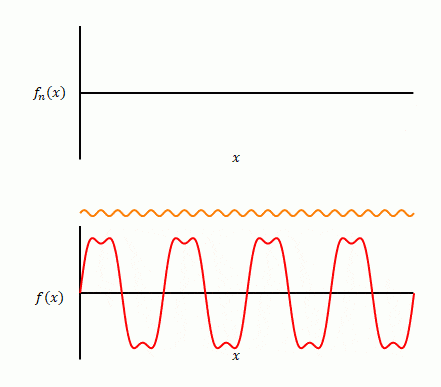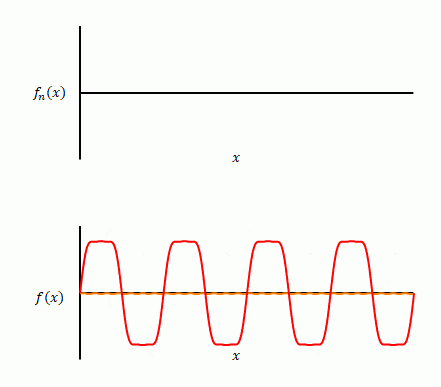
以上の例のように、特別な場合を除き、どのような関数でも三角関数の和として表すことができます。
なぜそうなるかはここでは省略します。後述のフーリエ級数を理解することによってその理由は理解できるかと思います。
3.2 重ね合わせの原理
関数\(f_2(x)\)と\(f_3(x)\)があります。フーリエ変換によってそれぞれ\(F(f_2(x))\)、\(F(f_3(x))\)が得られます。下の図のイメージです。
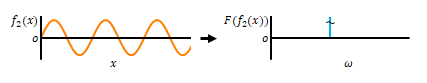

\(f_2(x)\)と\(f_3(x)\)の和を\(f(x)\)とします。このフーリエ変換後の関数\(F(f(x))\)は\(F(f_2(x))\)と\(F(f_3(x))\)と等しくなります。

これが重ね合わせの原理です。つまり、
$$F(f_2(x))+F(f_3(x))=F(f_2(x)+f_3(x))$$
が成立します。
したがって次のことがいえます。
単一の三角関数ではない\(f(x)\)をフーリエ変換する場合、\(f_2(x)\)と\(f_3(x)\)に分解し、それぞれをフーリエ変換し、その和を求めると、それが\(f(x)\)のフーリエ変換後の関数になります。
三角関数の大きさ(振幅)、周波数、位相がわかっているとフーリエ変換後の関数は容易に決定します。複雑な関数であっても三角関数に分解することによりフーリエ変換ができます。

重ね合わせの原理と似た言葉に「線形性」があります。厳密な区別は難しいのですが、線形性はフーリエ変換がもつ性質の一つと考えてください。また、物理学や工学に応用する場合は系にその性質があるかどうかという意味で使われることがあります。
※上の図の右側はフーリエ変換後の関数を意図していますが、完全ではありません(以下)。あくまでも重ね合わせの原理のイメージを表現することが目的なのでご了解ください。
・三角関数をフーリエ変換すると図の青のところはディラックのデルタ関数になります。青の部分に「~」がありますが、大きさを短縮する意味でつけています。
・負の領域を省略しています(正のみです)。
・それぞれ実数と虚数2つのグラフが必要ですが、一方のみを表示しています。
4 まとめ
・周波数:変数が1増えるごとに進む周期
・位相:関数の括弧中の値
・角周波数:変数が1増えるごとに進む角度
・特別な場合を除き、一定の周期で繰り返す関数は三角関数の和で表すことができます。
・関数を三角関数の和で表せるよう分解し、それぞれの三角関数をフーリエ変換し、和を求めると、それが元の関数のフーリエ変換後の関数です。これが重ね合わせの原理です。
補足:本文で触れていない説明
・三角関数には\(\tan\)などが含まれますが、ここではそれらを指すのではなく、\(\sin\)と\(\cos\)の意味で三角関数という言葉を使用する場合があります。
