ここまでフーリエ級数について述べてきました。次にフーリエ変換について説明します。ずいぶんフーリエ級数の説明が長かったと思われたかもしれません。
しかしフーリエ級数もフーリエ変換も本質の大部分は同じです。大部分は同じなのですが異なる部分もあります。複素フーリエ級数を元にフーリエ変換との相違点によってどのように定義が変わるかを考えましょう。
1 補足
1.1 周期が\(T\)の\(f(x)\)の複素フーリエ級数
「フーリエ変換4」 では複素フーリエ級数と係数の定義を述べましたが、これは\(f(x)\)の周期が\(2 \pi\)の場合のみに適用される式でした。\(2 \pi \)以外の場合にも適用できる式に変更します。
以下以下が「フーリエ変換4」で求めた式です。
$$f(x)= \displaystyle \sum_{n=-\infty}^{\infty} c_n e^{inx}$$
$$ c_n = \frac {1} {2\pi} \int_{-\pi}^{\pi} f(x) e^{-inx} dx$$
下図のように\(f(x)\)の周期が\(2\pi\)の場合のみ正しく級数展開できます。
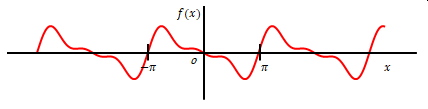
下図のように\(f(x)\)の周期が\(T\)の場合は上記式では正しい結果にはなりません。
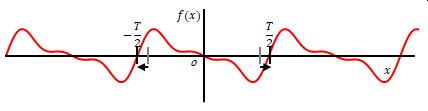
どう変更すればよいでしょう。
積分の外の\(\displaystyle \frac {1} {2\pi}\)は積分の区間の長さの逆数を示しています。積分の区間が\(2\pi\)から\(T\)に変わるので、この係数を\( \displaystyle \frac {1} {T}\)に変えます。
\(f(x)\)の式の\(e^{inx}\)も変えます。\(n=\pm 1\)のとき、積分の区間内で位相がちょうど1周(\(2 \pi\))変化するようにします。変更前の式は、積分区間\(-\pi\)から\(\pi\)に対し\(e^{inx}\)は\(2 \pi\)変化しています。
積分区間が\(- \displaystyle \frac {T}{2}\)から\( \displaystyle \frac {T}{2}\)の場合は\(e^{inx}\)を\(e^{ \frac{i2 \pi nx}{T}}\)に変えます。これにより\(n=\pm 1\)のとき積分区間内で\(-\pi\)から\(\pi\)変化するようになります。
\(c_n\)の\(e^{-inx}\)も同様に\(e^{ \frac{-i2 \pi nx}{T}}\)に変えます。
下の式が、周期が\(T\)の\(f(x)\)のフーリエ級数展開です。
$$f(x)= \displaystyle \sum_{n=-\infty}^{\infty} c_n e^{\frac{i2 \pi nx}{T}}$$
$$ c_n = \frac {1} {T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) e^{\frac{-i2 \pi nx}{T}}dx$$
1.2 複素フーリエ級数とフーリエ変換の違い
さて、フーリエ級数とフーリエ変換の違いは何でしょう。級数と変換という違いです。フーリエ級数はあくまでも関数を級数に展開したものです。これに対しフーリエ変換は別の関数に変換します。
これだけであれば単なる表現上の違いですが、もう一つ、根本的な違いがあります。フーリエ級数は周期関数のみ展開することができましたが、フーリエ変換は非周期関数も変換することができます。
1.3 フーリエ級数とフーリエ変換の変数・関数の対応
フーリエ変換の定義を導くために複素フーリエ級数を元に変形します。そこで、あくまで参考としてですが、フーリエ級数とフーリエ変換の変数・関数がどう対応するかを考えましょう。
複素フーリエ級数の\(c_n\)は特定の角周波数の成分を示します。フーリエ変換の\(F(\omega)\)も角周波数ごとの成分を示す関数です。
複素フーリエ級数における角周波数は指数部から\(x\)と\(i\)を除外した値で示されます。つまり、\( \displaystyle \frac{2 \pi n}{T}\)です。この中で値が変化するのは\(n\)のみです。 \(T\)はどのような値もとりえますが、級数の項ごとに変わることはないので固定といえます。\(F(\omega)\) の角周波数は\(\omega\)によって決まります。
つまり、以下のように対応します。左が複素フーリエ級数、右がフーリエ変換です。
\(f(x)\) → \(f(x)\)
\(c_n\) → \(F(\omega)\)
\(n\) → \(\omega\)
ただし、あくまで概念的なものであり、厳密には意味のあるものではありません。
2 複素フーリエ級数からフーリエ変換へ
2.1 積分区間を変更する
フーリエ級数とフーリエ変換では、扱える関数に違いがあります。フーリエ級数展開できるのは周期関数だけでした。フーリエ変換は非周期関数も対象です。
フーリエ級数では、 \(f(x)\) が周期関数であるからこれを別の周期関数(三角関数)の和として表すことができました。 フーリエ変換では非周期関数をどうやって変換するのでしょう。
\(c_n\)を求める式における積分区間を\(- \displaystyle \frac{T}{2}\)から\( \displaystyle \frac{T}{2}\)とすると、\(\left(m- \displaystyle \frac{1}{2}\right)T\)から\(\left(m+ \displaystyle \frac{1}{2}\right)T\)までの間の波形は\(- \displaystyle \frac{T}{2}\)から\( \displaystyle \frac{T}{2}\)の区間の波形と同じはずです(\(m\)は整数です)。しかし \(- \displaystyle \frac{T}{2}\)から\( \displaystyle \frac{T}{2}\) の間では任意の値をとることができます。
フーリエ変換では積分区間が異なります。\(-\infty\)から\(\infty\) とします。つまり、フーリエ級数における\( \displaystyle \frac{T}{2}\)を無限に大きくしたものと考えます。一つの積分区間の中に\(f(x)\)を収めてしまうので、\(f(x)\)を非周期関数とみなさなくてよいことになります。
2.2 指数の表現を変更する
\(c_n\)を求める式の中に\(e^{ \frac{-i2 \pi nx}{T}}\)という部分があります。\( \displaystyle \frac{2\pi nx}{T}\)は角周波数です。この角周波数をフーリエ変換では一つの変数として定義します。前述の仮定の通り、ここでは\(\omega\)とします。
\(T\)が無限大となるので\( \displaystyle \frac{\pi nx}{T}\)は無限小にはならないのでしょうか。
\(n\)は任意の値です。\(T\)を無限大に拡張するとき、以下のように\(\omega\)を一定に保つよう\(n\)を選択する、と考えれば任意の\(\omega\)に対応することは可能です。
$$ \displaystyle \lim_{T \to \infty} \frac{\pi n}{T} = \omega$$
2.3 フーリエ変換の定義
改めて、\(c_n\)を求める式が以下です。
$$ c_n = \frac {1} {T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) e^{\frac{-i2 \pi nx}{T}}dx$$
積分区間を\(-\infty\)から\(\infty\)、指数の係数を\(-i \omega x\)に変えます。
以上より以下の式に変形されます。
$$ F(\omega) = \int_{-\infty}^{\infty} f(x) e^{-i \omega x}dx$$
これがフーリエ変換です。
2.4 面積が有限の非周期関数をフーリエ変換すると無限小になるのでは?
フーリエ級数では積分した値を積分区間の長さで割っていました。\(- \displaystyle \frac{T}{2}\)から\( \displaystyle \frac{T}{2}\)で積分する場合は\(T\)です。もし下の図のように面積が有限である\(f(x)\)を無限に大きい\(T\)で割ると限りなく0に近くなります。面積が有限値の関数はフーリエ変換できないのでしょうか。
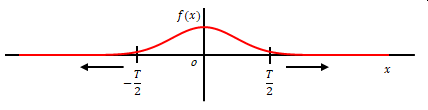
前項の定義で説明しませんでしたが、 フーリエ変換では積分区間の長さで割りません。積分したままなのです(\(\sqrt {2 \pi} \)で割る場合はあります)。これであれば積分値が有限である関数の変換後の値が無限小になることはありません。
フーリエ級数の係数からフーリエ変換の関数に変形する過程で係数\( \displaystyle \frac{1}{T}\)の違いが生じますが、問題はないのでしょうか。
これはフーリエ変換の定義であって、何かの制約があるわけではありません。ただし後述しますが、フーリエ逆変換によって元の関数に戻るよう両者の関係は保つ必要はあります。
2.5 周期関数をフーリエ変換すると無限大になるのでは?
前項で、フーリエ変換では無限大の\(T\) では割らないので面積が有限の非周期関数が無限小となることはないと述べました。
しかし今度は周期関数をフーリエ変換すると無限大になるのではないでしょうか。
その通りで、非周期関数をフーリエ変換するとその周波数で無限大になります。また、その周波数の整数倍の成分を含んでいる場合はそれも無限大になります。
変数がある値のときのみ無限大で、それ以外のときは0という状態を表す関数があります。これをデルタ関数(ディラックのデルタ関数)とよびます。デルタ関数を用いて三角関数のフーリエ変換を表します。
デルタ関数の定義です。
\(x=0\)のとき
\(\delta(x)=\infty\)
\(x \neq 0\)のとき
\(\delta(x)=0\)
ただし、
\(\displaystyle \int_{-\infty}^{\infty}\delta(x)dx=1\)
これを用いて\(f(x)=\cos qx\)をフーリエ変換すると、
$$F(\omega)=\pi ( \delta(\omega – q) + \delta (\omega + q))$$
となります。
\(f(x)=\sin qx\)をフーリエ変換すると、
$$F(\omega)=i\pi ( \delta(\omega + q) – \delta (\omega – q))$$
となります。
\(f(x)=\cos qx\)のフーリエ変換の詳細は「+」を展開し確認してください。
3 フーリエ級数からフーリエ逆変換へ
3.1 変数を置き換える
次は逆フーリエ変換です。
まず、改めて複素フーリエ級数と係数の定義です。
$$f(x)= \displaystyle \sum_{n=-\infty}^{\infty} c_n e^{\frac{i2 \pi nx}{T}}$$
$$ c_n = \frac {1} {T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) e^{\frac{-i2 \pi nx}{T}}dx$$
フーリエ級数では\(f(x)\)を\(c_n\)の式で表しました。フーリエ逆変換では\(f(x)\)を\(F(\omega )\)の式で表します。単に変数・関数を置き換えるだけではありません。\(f(x)\)が非周期関数であっても逆変換できなければなりません。そのためにどのように変形するかを考えてみましょう。
\(c_n\)の実部をグラフにすると下の図のようになります。この段階では\(T\)は有限です。横軸は\(n\)です。
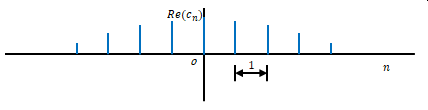
虚部も関わってくるのですが、実部と考え方は同じです。以下、実部だけを考えてみます。
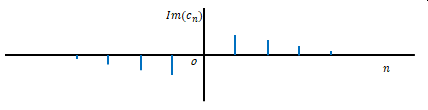
グラフの横軸を\( \displaystyle \frac{2 \pi n}{T}\)に変えます。
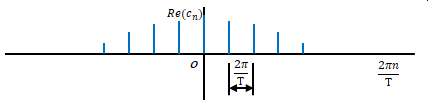
周期関数なので飛び飛びに値が存在します。横軸における最小間隔は以下です。
$$\frac{2 \pi (n+1)}{T}-\frac{2 \pi n}{T}=\frac{2 \pi }{T}$$
\( \displaystyle \frac{2 \pi n}{T}\)は角速度、つまり\(\omega\)でした。グラフの横軸をこれに置き換えます。値が存在する最小間隔は\(\Delta \omega \)とします。
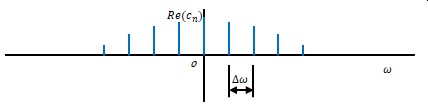
3.2 \(f(x)\)を周期関数から非周期関数へ変える
ここまでは\(f(x)\)を周期関数としていました。フーリエ級数で表すことのできる関数です。グラフ上では飛び飛びの棒となって現れる値の和が\(f(x)\)でした。
ここからは\(f(x)\)が周期関数ではなく非周期関数だった場合を考えてみます。縦軸は\(c_n\)ではなく、\(F(\omega)\)で表します。
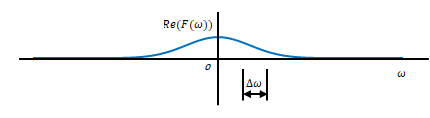
\(\omega\)の変化に対し\(F(\omega)\)は連続した値となります。
3.3 \(F(\omega)\)の総和を求める
周期関数では特定の位置で示す値の和として\(f(x)\)を表しました。しかし連続になると和で表すことができなくなります。どうやって\(f(x)\)を表せばよいでしょう。
\(f(x)\)は和ではなく、面積とすればよいのです。
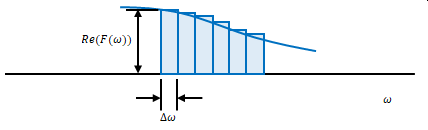
図のように横軸を\(\Delta \omega \)で区切り、その区間の長方形の面積の和を求めます。
なめらかに変化する関数を長方形の面積の和で求めようとすると誤差があるように思えます。しかしフーリエ変換では\(T\)を無限大にしました。フーリエ逆変換でも \(T\)を無限大にしま す。
\(\Delta \omega = \displaystyle \frac{2 \pi }{T}\)です。\(T\)が無限大になれば\(\Delta \omega\)は無限小になります。短辺が無限に小さい長方形が無限に存在することになります。
このように変数を無限に小さく区切って関数の値との積の和を求める操作は積分ですね。
\( \displaystyle \sum_{n=-\infty}^{\infty}\)だったところが\(\displaystyle \int_{-\infty}^{\infty}\)に変わります。
図では変数の最小区間は\(\Delta \omega\)でした。これを無限小に変えることにより\( d\omega \)になります。
フーリエ変換のときと同じく、\(c_n\)を\(F(\omega)\)に置き換えます。\(e^{ \frac{i2 \pi nx}{T}}\)だったところは\(e^{i \omega x }\)に変わります。
これで以下のような式になります。積分の外の係数が何か必要かもしれませんがこの時点で不明なので、仮に\(p\)としておきます。
$$ f(x) = p \int_{-\infty}^{\infty} F(\omega) e^{i \omega x }d\omega$$
3.4 係数を求める
さて、複素フーリエ級数の式から変数・関数を変えて直前の式にしましたがこの式の中に、フーリエ級数にはない変数があります。
\(\Delta \omega\)(積分の式では\(d \omega\))です。
\(F(\omega)\)が とびとびの関数の値であれば和を求めるだけでよかったのですが、連続する関数の場合のために面積を求めることにしました。面積を求めるために縦軸と横軸を掛けます。それが\(\Delta \omega\)でした。
これも定義の問題なので、\(\Delta \omega\)を追加すること自体は問題ではありません。ただし、フーリエ変換した関数をフーリエ逆変換、あるいはその逆をした結果が元の関数と一致するような係数でなければなりません。
では係数が一致するためにどうするか考えましょう。フーリエ変換まで遡り\(\Delta \omega\)の他に、複素フーリエ級数係数に関わる操作がなかったでしょうか。
フーリエ変換における\( \displaystyle \frac{1}{T}\)です。
整理すると、複素フーリエ級数の係数からフーリエ変換に変形する過程で\( \displaystyle \frac{1}{T}\)を削除し、複素フーリエ級数からフーリエ逆変換に変形する過程で\(\Delta \omega\)を追加しました。
フーリエ逆変換の式導出時に\(\Delta \omega = \displaystyle \frac{2\pi}{T}\)と定義しています。
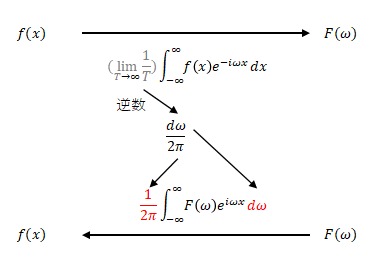
フーリエ変換の過程で\( \displaystyle \frac{1}{T}\)を削除したので、その分の補正としてフーリエ逆変換では逆数の\(T\)を追加します。
フーリエ逆変換で追加した \(\Delta \omega \)(積分では\(d \omega \))はどうすればいよいでしょう。
\(T\) の一部と \(\Delta \omega \) を相殺します。
\(T\)を\(\omega\)で表すと\(T= \displaystyle \frac{\Delta \omega}{2 \pi}\)となります。既に求めたフーリエ逆変換の仮の式の中で既に\(\Delta \omega \)(積分では\(d \omega \))を追加しています。
あとは足りない分としてフーリエ逆変換で積分した値を\(2 \pi\)で割ります。係数の移動をイメージで表すと以下のようになります。
3.5 フーリエ逆変換の定義
前述の式の\(p\)は\( \displaystyle \frac{1}{2\pi}\)でした。これでフーリエ変換とフーリエ逆変換を何回繰り返しても係数は一致します。フーリエ逆変換の式は以下になります。
$$ f(x) = \displaystyle \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega) e^{i \omega x }d\omega$$
4 その他
4.1 フーリエ変換とフーリエ逆変換の係数
何度か言及しましたが、フーリエ変換前の関数とフーリエ変換後の関数のスケールには数学上の制約があるわけではありません。変換を往復させたときに変換後の関数と元の関数と一致するようになっていれば何でもよいはずです。あとはどう定義するかだけの問題です。実際、定義は一通りではありません。
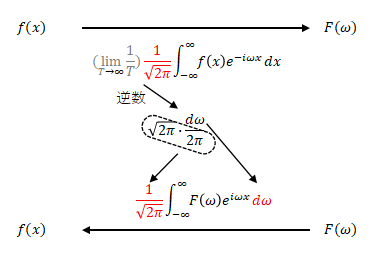
ここではフーリエ変換の係数がないようにしました。その代わり、フーリエ逆変換では\( \displaystyle \frac{1}{2\pi}\)という係数がつきました。
両者の係数を同じ値とする定義もあります。つまり\( \displaystyle \frac{1}{\sqrt{2\pi}}\)です。
式は以下です。
$$ F(\omega) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} f(x) e^{-i \omega x}dx$$
$$ f(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} F(\omega) e^{i \omega x }d\omega$$
前述のイメージは以下のように変わります。
4.2 フーリエ変換後の関数は複素数?
「フーリエ変換4」で、複素フーリエ級数の係数は複素数だが、展開した級数は実数だと述べました。
フーリエ変換でも同じことがいえます。\(f(x)\)が実数であったとしてもフーリエ変換した\(F(\omega)\)は複素数です。 \(F(\omega)\) をフーリエ逆変換すると、\(f(x)\)となることからもわかるように実数です。
5 まとめと補足
5.1 定義
・\(f(x)\)の周期が\(T\)の場合はフーリエ級数の定義は以下です。
$$f(x)= \displaystyle \sum_{n=-\infty}^{\infty} c_n e^{\frac{i2 \pi nx}{T}}$$
$$ c_n = \frac {1} {T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) e^{\frac{-i2 \pi nx}{T}}dx$$
・フーリエ変換とフーリエ逆変換の定義は以下です。
$$ F(\omega) = \int_{-\infty}^{\infty} f(x) e^{-i \omega x}dx$$
$$ f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega) e^{i \omega x }d\omega$$
・フーリエ変換とフーリエ変換の定義は以下のように異なる係数で表す場合もあります。
$$ F(\omega) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} f(x) e^{-i \omega x}dx$$
$$ f(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} F(\omega) e^{i \omega x }d\omega$$
5.2 その他
本ページではフーリエ級数からフーリエ変換・フーリエ逆変換を導きました。
\(c_n\)の定義式を非周期関数対応に拡張させるために、積分の周期を\(-\infty\)から\(\infty\)に広げ、\(n\)を添え字とする係数ではなく、\(\omega\)の関数で表しました。これがフーリエ変換です。
\(f(x)\)の定義式を非周期関数対応に拡張させるために、各角周波数の項の和で表していたところを角周波数で積分する形式に変えたのがフーリエ逆変換です。
5.3 補足:本文で触れていない事項
・\(f(x)\)をフーリエ変換した関数を\(F(\omega)\)と定義しました。しかし記法は他にもあります。\(f(x)\)をフーリエ変換した関数という意味で対象の関数に\(\hat{}\)をつけることがあります。今の場合では\(\hat{f}(\omega)\)となります。また、\(f(x)\)のフーリエ変換という意味で\(\mathcal{F}[f(x)]\)と表す場合もあります。本サイトではこれらを使わず、\(F(\omega)\)のように大文字の関数で表しています。
