フーリエ変換６（周波数伝達関数） | 試験に出ない科学の話

「フーリエ変換1-5」ではフーリエ級数とフーリエ変換の定義について説明してきましたが、ここでは実際に使われる例として周波数伝達関数（以下、伝達関数）を使った解析について取り上げます。伝達関数はフーリエ変換とは直接関係ありませんが、信号処理などの分野では両者が密接にかかわります。

フーリエ級数とフーリエ変換は純粋な理論であって実用のためのものではありません。伝達関数と組み合わせて使うには少し不便なところがあります。理論を応用するために多少の手直しが必要です。

そこでここではいくつかの前置きを述べています。真面目に理解しようとするとかなり長くなります。とりあえずは「そのようなもの」と思って深入りしなくてもよいかもしれません。

1 補足

1.1 極座標表示

まず一つ目の予備知識として極座標表示について説明します。

複素数とは何でしょうか。

実数と虚数からなる数ですね。以下のように表すことができます。

$$z = a + ib$$

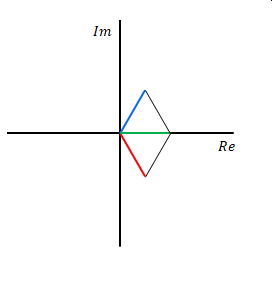
括弧を使って$a,b)$と表すこともあります。複素平面では下の図の位置です。

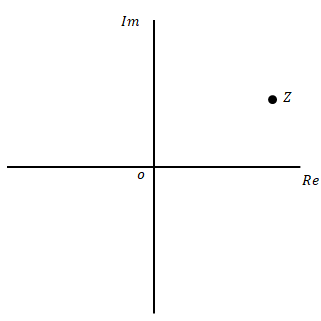
これらの表示は直交座標表示とよばれます。

しかし複素数を表す方法は直交座標だけとは限りません。2種類の実数の組み合わせであれば直交座標以外の方法で表すことができるものがあります。その一つが極座標表示です。

下の図を見てください。

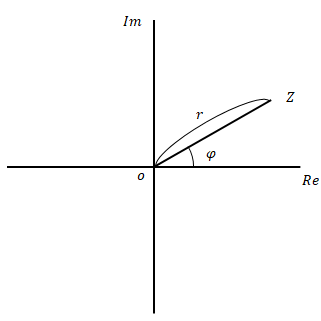
この$z$の、絶対値（0からの距離）と偏角（実軸となす角）が極座標です。

式では

$$z= r e ^ {i \phi}$$

と表すことができます。

括弧を用いると

$r,\phi$

となります。

極座標表示と直交座標表示は複素数の表示形式が変わるだけです。複素数の値が変わるわけではありません。また、極座標も一般的には直交座標と同じ複素平面を使います。

1.2 正の周波数のみを使用する

もう一つ予備知識です。

複素フーリエ級数の係数やフーリエ変換後の関数では正だけでなく負の周波数も必要とします。しかし、この後の説明では負の周波数を省略します。正の周波数のみを使用します。スケールを合わせるために複素フーリエ級数の場合、係数を2倍にした値を使用します。詳細は「＋」を押して展開してください。

正の周波数だけで表示する

ここでは複素フーリエ級数やフーリエ変換をそのまま使わず、正の周波数のみで表す方法について考えます。意外に複雑で長くなる一方、重要な目的があるわけではないので、読み飛ばしてもよいかもしれません。

(a)正の周波数だけで表示できる？
実フーリエ級数、複素フーリエ級数、フーリエ変換の中で負の周波数を使用しないのはどれでしょうか。
実フーリエ級数ですね。
複素フーリエ級数とフーリエ変換は負の周波数を使用します。
理論上、負の周波数が登場することはなんら問題ではありませんが、実用上はなるべく簡潔に表現したいものです。正の周波数だけで表現できないものでしょうか。
負の周波数を使わない実フーリエ級数を使うのはどうでしょう。これはこれで三角関数を使わないといけないという問題があります。三角関数は演算するたびに$sin$と$cos$が入れ替わり複雑になります。できれば複素数と指数関数の組み合わせを使いたいところです。
複素フーリエ級数とフーリエ変換では正の周波数と負の周波数の成分は複素共役の関係にあります。独立の関係ではありません。これらをまとめて正の周波数だけで表示できそうです。
次の項ではその方法について述べます。

(b)ベクトル表示
電気工学では正弦波を表すために「ベクトル表示」という方法を用いることがあります。これは正弦波をベクトルで表示することですが、通常、正の周波数のみを使用します。
以下のように関数が定義されているとします。
$$x(t)=r\sin (t + \phi)$$
$x(0)$を複素数を用いて$z=r e^{i\phi}$と表すと、これがベクトル表示です。極座標では$(r,\phi)$、複素平面では下の図の通りです。

これは前項の極座標の図のそのものです。ベクトル表示自体は固定の複素数を極座標で表しているだけです。変数に合わせて動くものではありません。しかし周期が既知であれば三角関数が一意に決まるので、このような表示だけで済むという考え方です。
この固定値からどうやって$x(t)$が決まるのでしょう。
$x=0$のときにこのベクトルの値で、$x$の増加とともに複素平面上を周期$2\pi$で反時計回りに移動する関数があるとします。その虚部が$x(t)$です。
$$x(t)=Im(e^{i\phi + t}) $$
複素平面上の$x(t)$は次の項で示します。

(c)複素フーリエ級数の係数とベクトル表示の関係
$x(t)=r\sin (t + \phi)$を複素フーリエ級数に展開すると以下になります。
$$x(t)=c_{-1} e^{-it} + c_{1} e^{it}$$
$$c_{-1} = -i\frac { r e^{-i\phi} } {2}$$
$$c_{1} = i\frac { r e^{i\phi} } {2}$$

これらを複素平面で表してみましょう。
下の図の左側が複素フーリエ級数の係数です。右側がベクトル表示です。

どちらも緑色の部分が$t(0)$です。
わかりにくいかもしれませんが、左の図を反時計回りに90度回転させてみれば一致します。
次の図は$t$を増やしていったところです。

$t=0$以外においても一致することがわかります。
フーリエ級数の係数とベクトル表示はどういう関係にあるでしょう。
もう一度、上の図をみてください。
二つのフーリエ級数は複素共役の関係にあります。足すと実部だけが残ります。これが$t(0)$です。
一方、ベクトル表示の場合は虚部が同じく$t(0)$です。
$c_1$が虚軸となす角、ベクトルが実軸となす角はどちらも$\phi$です。
したがって、複素フーリエ級数$c_1$を2倍した複素数がベクトルです。$c_{-1}$は不要です。
$$r=2|c_1|$$
$$\phi=\arg i c_1$$
argは複素数と原点を結ぶ線と実軸がなす角のことで偏角とよびます。iを掛けているのは半時計回りに90度回転させることを示しています。
以上が$x(t)$が単純な正弦波の場合に正の係数のみで表すことができる理由です。
$x(t)$が複数の周波数の正弦波が重畳している関数の場合は、それぞれの周波数において同じように係数とベクトルが対応します。
$$r_n=2|c_n|$$
$$\phi_n=\arg i c_n$$
とすると複素フーリエ級数を変形して$x(t)$を以下のように表すことができます。
$$x(t)= Im(\displaystyle \sum_{n=0}^{\infty} r_ n e^{i(nt + \phi_n)})$$
同様にフーリエ変換を変形してベクトルで表すこともできますが省略します。

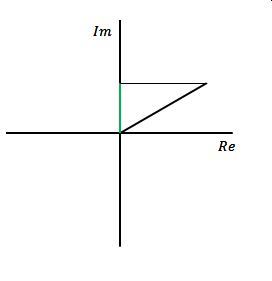
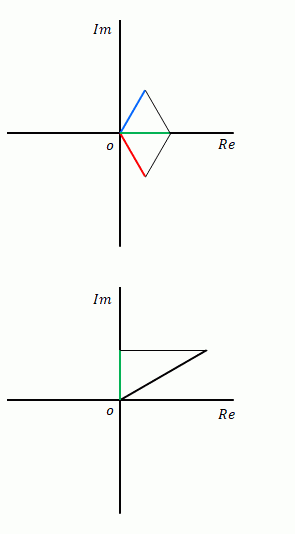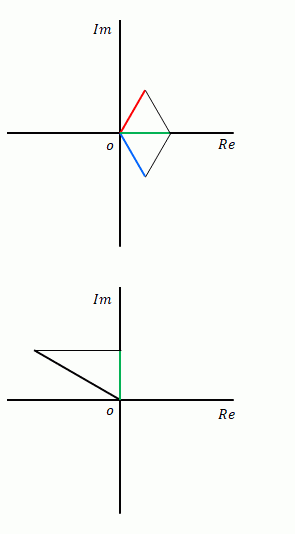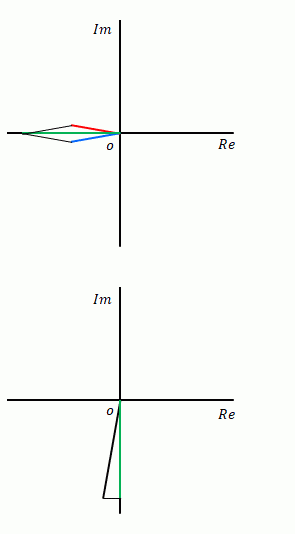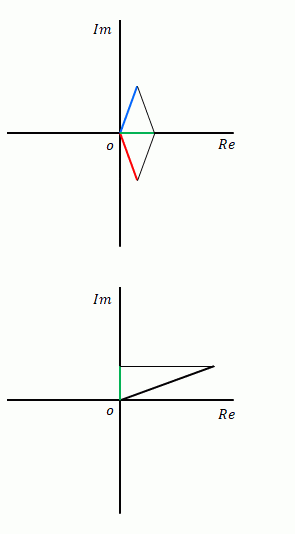
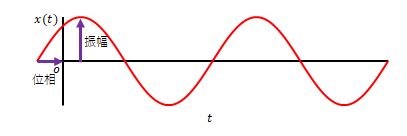
ここでは前項の極座標を使って正弦波を下の図のように表します。また、ここでは波の大きさを「振幅」とよびます。物理学や工学では一般的に使われている用語です。既に使われていますが、基準となる正弦波（この場合、時間0で値が0となる正弦波）からの時間のずれを角度で表した量を「位相」とよんでいます。

2 伝達関数

2.1 糸電話の例

さて、糸電話を例として考えてみます。

送信側の音がコップ・糸を振動させ受信側に届きます。しかし受信側のコップから聞こえてくる音は話者の声とは少し違いますね。受信側の音はコップと糸を通る間に変化しているからです。

送信側の音から受信側の音を再現できるでしょうか。もちろん糸電話の物理的な性質（特性）がわかっていなければいけません。どのような特性が必要で、どのような方法で再現するかをこれから考えていきましょう。

2.2 補足1：この後の説明における製薬

この例を説明するうえでいくつか制約と補足があります。

・音は空気の中を疎密波として通りますが、この度合いを$x(t)$として表します。$t$は時間です。

・$x(t)$を周期関数として説明したいため、フーリエ級数を使用します。フーリエ変換で表すとデルタ関数が関わりややこしくなるで避けます。

・一般的には伝達関数は極座標表示で表します。伝達関数の場合は利得と位相差（または単に位相）とよびます。必ず両者が必要なのですが、この後の例では位相が常に0とし、利得のみが周波数によって変化するものとします。

・周波数領域のグラフは対数で表すことが多いのですが、より直感的にわかるよう、ここでは線形としています。

2.3 送信側の音の定義

送信側が次のようであったとします。

800Hz（1600π rad/s）、2400Hz（4800π rad/s）、4000Hz（8000π rad/s）の正弦波が1:0.8:0.7の大きさの比で含まれていたとします。これらの成分の位相は全て0とします。

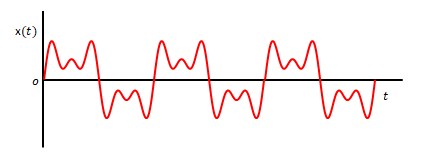
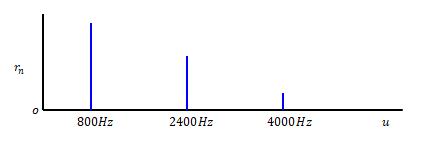
これをフーリエ級数で表したのが下の図です。横軸は周波数$u$です。角周波数$\omega$を併記しています。負の周波数は省略しています。フーリエ級数は800Hzのときに$n=1$です。$r_n$は複素フーリエ級数の係数$c_n$の絶対値の2倍です。正の周波数だけで表示するためにベクトル表示とし$r_n$を使っています。

縦軸は波の大きさです。

2.4 必要な糸電話の特性とは？

冒頭で述べたように糸電話の特性がわからないとその先の音の知りようがありません。ではどのような特性が必要でしょう。

何か必要というなら受信側の音がわかればいいのではないでしょうか。これならそもそもフーリエ級数もフーリエ変換も必要ありません。

しかしそこで得た音は特定の送信側の音のみに対応します。音の種類は無限にあります。送信側の音が少しでも変われば受信側の音がどう変わるかを予測できません。ではどうすればよいのでしょう。

正弦波に分解すればよいのです。どのような波であっても正弦波に分解できます。もしその正弦波の周波数が同じであれば糸電話を通った後の音は同じです。もちろん、周波数が異なれば伝わり方は異なるので送信側の音に含まれる正弦波の周波数全ての伝わり方が必要です。しかしその情報さえあれば演算にて受信側の音が分かります。

2.5 正弦波に分けて伝わり方を調べる

800Hzの正弦波の音を送信側のコップに向けるとどうなるでしょう。800Hzというのは人間の話し声程度です。受信側のコップではよく聞き取れるはずです。

では2400Hzの音ではどうでしょう。ソプラノの声より少し高いぐらいです。受信側の音量は送信側より少し小さくなるかもしれません。ここで注意していただきたいのは、2400Hzの成分が800Hzより小さい、ということではありません。2400Hzの正弦波が糸電話を通して減衰する、ということです。

4000Hzではどうでしょう。スズムシの鳴き声がこれぐらいです。受信側の音量はさらに小さくなるはずです。

2.6 伝達関数とは

前項では周波数によって音の伝わりやすさが違うことを述べました。伝わりやすさは角周波数領域（周波数領域）における出力関数（この場合受信側の音）を入力関数（送信側の音）で割った値として表すことができます。図の例では、$\frac{b}{a}$です。

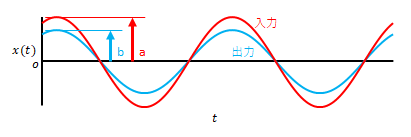
上記は入力が正弦波の場合についてでしたが、複数の周波数の正弦波が重畳している場合はどのように表すことができるでしょう。

正弦波に分けてそれぞれの周波数においてこの比を表わすことができます。これが伝達関数です。

伝達関数を$G(u)$とします。$u$は周波数です。下の図のように、横軸を周波数、縦軸を$G(u)$として表すことができます。

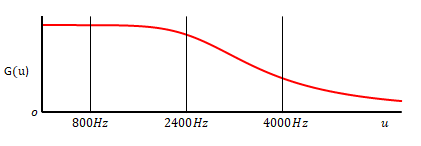
2.7 受信側の音を求める

伝達関数と送信側の音が分かれば受信側の音を演算で求めることができます。出力（受信側の音）を入力（送信側の音）で割った値が伝達関数でした。つまり、送信側の音に伝達関数を掛ければ受信側の音になります。

ただし直接、時間領域の音が得られるわけではありません。伝達関数は周波数領域（各周波数領域）で表されます。送信側も周波数領域で表したものでなければなりません。この例では送信側の音をフーリエ級数展開しています。両者を掛けることにより、受信側のフーリエ級数が得られます。

受信側のフーリエ級数の係数を$s_n$とします。2.3節のフーリエ級数と2.6節の伝達関数を掛けると下の図になります。

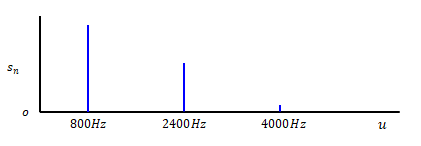
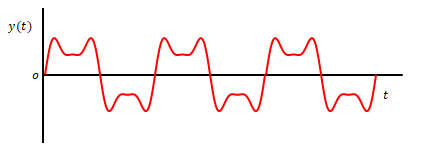
$s_n$から求めた時間領域の関数（ここでは$y(t)$とします）が受信側の音です。送信側の波形より変化している点に注目ください。

2.8 伝達関数の位相成分

2.3節から2.7節までが伝達関数を使った例です。しかしこれは特殊な場合です。位相（位相差）を0としているからです。ここでの位相は送信側の音と受信側の音の位相の差のことです。入力に対して出力が遅れた場合は負の角度で表します。

前述の例は振幅（波の大きさ）の比を伝達関数としましたが、この位相も伝達関数の一部です。位相のある正弦波を表すとき、$sin$と$cos$の成分、複素数の直交座標表示、複素数の極座標表示などの方法がありました。伝達関数も同様にいずれの方法かの表示が可能ですが極座標表示が一般的です。この場合、振幅の比は一般的に利得とよばれます。位相の差はそのまま位相差か位相です。

伝達関数における位相は図の$\frac{2\pi b}{a}$です。$b$の矢印が左向きになっていますが、負の値であることを示すためにこのようにしています。定義にもよりますが、実際には入力に対して出力は遅れます。遅れた場合は負とします。

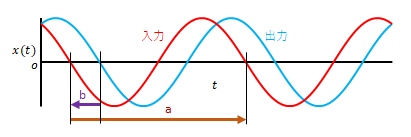
通常、位相は0ではありません。入力に対して出力は遅延があります。この遅延を角度で表したものが位相だからです。しかも位相は周波数（角周波数）によって異なります。ある場合を除き位相によっても出力の波形は変化します。ではある場合とはどのような場合でしょう。位相に角速度を掛けた値が周波数（角周波数）に限らず一定の場合です。この場合、遅延が一定だからです。

このような場合は特殊で、通常、遅延は一定となりません。周波数領域（角周波数領域）における位相の特性によって時間領域の波形にどう影響があるかを直感的に把握するのは少し難しいので省略します。

2.9 一般的な説明

以下のように定義します。
入力の関数：$x(t)$　これをフーリエ変換した関数：$X(\omega)$
伝達関数：$G(\omega)$
出力の関数：$y(t)$　これをフーリエ変換した関数：$Y(\omega)$

※フーリエ級数ではなく、フーリエ変換を使用します。また、周波数ではなく、角周波数にします。周波数が一般的でないわけではありませんが、ここでは前ページまでの説明に合わせます。

※前項の説明の通り、$G(\omega)$は2種類の値を含みます。一般的には利得と位相で表します。

出力の周波数領域の関数は以下で求められます。

$$Y(\omega) = G(\omega)X(\omega)$$

これをフーリエ逆変換すると$y(t)$が求められます。

2.10 離散フーリエ変換

伝達関数の話は以上です。最後にシミュレーションをします。その前にもう一つだけ説明があります。

これまで$x(t)$は連続した値を取るという前提で説明してきました。つまり$t$の増加によって$x(t)$が連続して変化します。

しかし、この後の例では$x$が一定の間隔で増えたところでのみ値をもつこととします。例えば、$x(1)$、$x(2)$、$x(3)$…というように整数に対しては値をもつが、1と2の間、2と3の間など整数以外の値をもたない、というような関数です。

なぜわざわざ定義を変えるかというと、デジタル信号処理に合わせるためです。デジタルとは値がとびとびということですが、同時にこれを処理する回路や伝達するメディア内ではほとんどの場合で一定の時間間隔で値が変化するようになっています。まさに前述のような動作をしています。こうすることによって情報量を減らすことができ、テジタル回路はこのような処理が得意だからです。

そしてフーリエ変換と似た概念もあります。これは離散フーリエ変換と呼ばれます。

ただし離散フーリエ変換とフーリエ変換では異なるところがあります。それは$x(t)$が周期関数であったとしても「離散フーリエ変換」後の関数の値は有限だということです。周期関数を「フーリエ変換」すると必ずデルタ関数が必要になります。つまりある変数において無限の値になります。しかし離散フーリエ変換ではデルタ関数はでてきません。すべて有限の値です。

離散フーリエ変換における$x(t)$の対象の範囲が有限だからです。フーリエ変換では範囲が無限なので周期関数を変換すると無限の値が生じます。離散フーリエ変換ではこのようなことがありません。離散フーリエ変換の範囲が有限なのは実用においては信号が有限長だからなのでしょう。

3 シミュレーション

では実際に音を出して伝達関数通過による違いを確認してみましょう。

実行すると音が出るのでご注意ください。

下の画面の最下部にボタンがあります。縦に長くなってボタンが隠れているかもしれませんので、見当たらない場合はスクロールして表示してください。

ボタンの意味は以下です。

開始：最初に押してください。
入力：ランダムに入力の波形を変えます。同時に音を出力します。
周波数：基本となる周波数（最も低い周波数成分）を440Hz→660Hz→880Hz→1100Hz→440Hz→…と変えます。
伝達関数：伝達関数を変えます。伝達関数はローパスフィルタとハイパスフィルタ（後述）の2種類です。
繰返：同じ設定で再度出力します。

最初に「開始」ボタンを押してください。この時点では何も反応がありません。その後「開始」以外のいずれかのボタンを押すと音を出力します。「開始」ボタンの代わりに他のボタンを押しても同様に次の操作から出力を開始します。UI上は全く必然性のない操作ですが、プログラムの都合によりこのようにしています。ご了解ください。

「開始」ボタンを押した後はボタンを押すごとに入力の音を2秒、その後に出力の音を2秒出力します。

グラフは以下の意味です。

音量

説明を保留にしていましたが、ここでは伝達関数をローバスフィルタとハイパスフィルタの2種類より選ぶようにしています。ローパスフィルタとは低い周波数領域の信号は通し、高い周波数の信号は減衰させるフィルタです。ハイパスフィルタはその逆です。伝達関数の利得の特性を見るとその違いがわかると思います。

ローパスフィルタを通した場合、出力の波形（$g(t)$）はなだらかに変化するようになります。一般的に音はこもったようになります。

ハイパスフィルタを通した場合、出力の波形は速く変化する成分が協調されるようになります。一般的に音はささくれだったようになります。

4 まとめと補足

4.1 まとめ

本ページでは、フーリエ変換を使った例として、伝達関数を組み合わせた解析方法を説明しました。その流れは2章の通りです。

ここでは糸電話を例にしましたが、身の回りにはいたるところに波が存在します。波が伝播すると変化します。その変化は周波数によって決まります。これを表すのが伝達関数です。

もちろんただ表すだけではなく、発生源の波（入力の関数）と伝達関数の演算により、変化した後の波（出力の関数）を計算で求めることができます。

その演算とは以下2種類です。

・入力の振幅と伝達関数の利得を掛け算すると出力の振幅が得られる。
・入力の位相と伝達関数の位相を足し算すると出力の位相が得られる。

これをフーリエ逆変換すると時間領域の波が得られます。

大まかな伝達関数の目的は以上です。前提のための説明が長くなってしまいました。細かいことにこだわる必要はないとは思いますが、混乱を避けるため、改めてここでまとめます。

・フーリエ変換した後の関数や複素フーリエ級数の係数は一般的には直交座標ではなく極座標を用いる（後述）。
・複素フーリエ級数とフーリエ変換では正と負の周波数を用いるが、ここでは正の周波数のみを用いた。
・糸電話の例では角周波数ではなく周波数を用いたが角周波数でも同じように表現できる。
・このページのシミュレーションではフーリエ変換ではなく離散フーリエ変換を使用した。離散フーリエ変換では周波数領域のすべての値は有限である。

4.2 補足1：出力を求めるために必ずフーリエ変換・逆変換が必要？

本ページでは時間の関数をフーリエ変換して伝達関数と演算子フーリエ逆変換をする手順を紹介しました。しかしなぜわざわざフーリエ変換し演算してからフーリエ逆変換しないといけないのでしょうか。

伝達関数は角周波数（周波数）の関数として定義されます。しかし時間領域において伝達関数に相当する関数を定義することはできます。伝達関数をフーリエ逆変換するとその関数が得られます。この関数から出力を求める方法もあります。

しかし次のような関係にはなりません（上記の関数を$g(t)$とします）。

$$y(t)=g(t)x(t)$$

もう少し複雑な演算が必要です。どのような演算なのかについては省略します。

4.3 補足2：なぜ極座標表示が使われる？

波を周波数領域で表わすには2種類の数が必要です。一つの方法は実フーリエ級数のように$sin$と$cos$の係数として表わす方法です。この方法は伝達関数を用いた解析の分野ではあまり用いられません。また、複素フーリエ級数やフーリエ変換のように複素数で表すことができます。この場合でも直交座標表示はあまり使われません。よく使われるのは極座標表示です。極座標表示のほうが都合がよいからなのでしょう。では何がよいのででしょう。

まず考えられるのは、波の大きさが一目でわかる点です。直交座標でももちろんわかりますが絶対値を求めなければいけません。極座標には絶対値が含まれます。これが波の大きさそのものです。

また、複素数の掛け算が容易ということもあるでしょう。複素数の掛け算を思い出してください。極座標表示の場合、絶対値どうしを掛け算、偏角どうしを足し算すればよいのです。