フーリエ変換について調べていると「畳み込み」や「インパルス応答」の説明が出てくることがあるかと思います。これらはフーリエ変換の定義そのものではありませんが深い関係があるのでフーリエ変換の一部として取り上げられるのでしょう。
初見ではなかなかピンとこないのではないかと思います。あまり深く意味を知らなくてもよいかもしれません。
しかし、意味がわかっていればその先のことも理解しやすいかもしれません。じっくりと考えてみましょう。
※ここでは 時不変システム における畳み込みとインパルス応答の関係に限定して説明します。
1 インパルス応答
1.1 インパルス応答の例
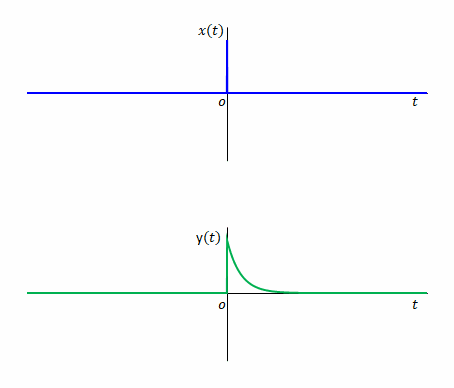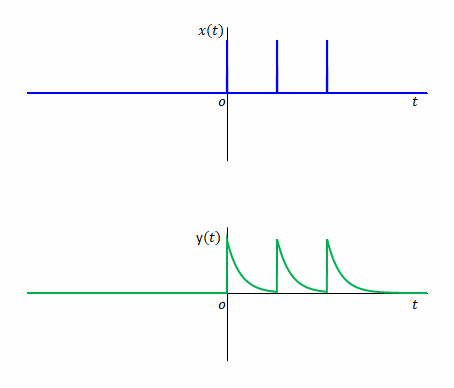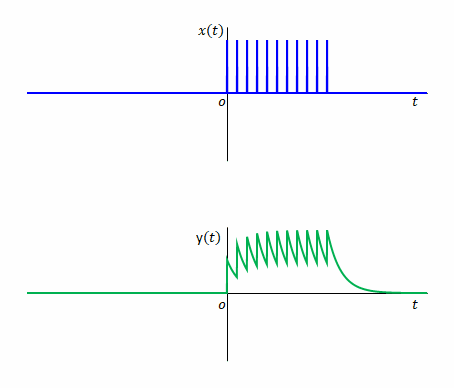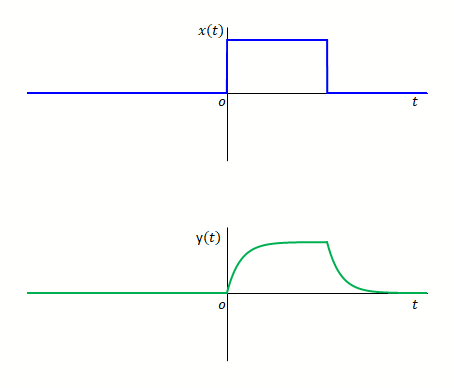
次のような系を考えます。
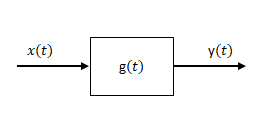
\(x(t)\)がディラックのデルタ関数であったとします(以下)。
\(t=0\)のとき
\(\delta(t)=\infty\)
\(t \neq 0\)のとき
\(\delta(t)=0\)
ただし、
\(\displaystyle \int_{-\infty}^{\infty}\delta(t)dt=1\)
下の図は面積を変えずにパルスの幅を減少させ、大きさを増加させる様子を意図しています。パルス幅が無限小、大きさが無限大となった状態が\(\delta(0)\)です。
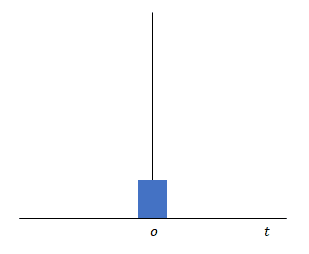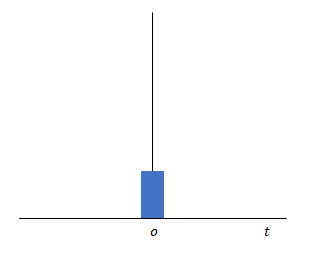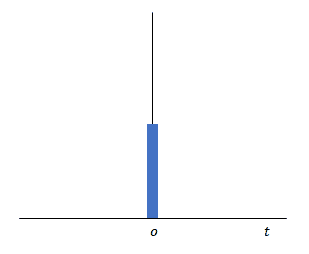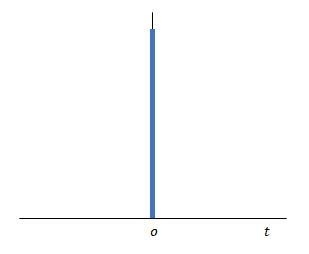
わずかな\(t\)の増分の間に生じるパルスであることからこれをインパルスとよびます。
\(t=0\)における\(x(t)\)のインパルスによって生じる\(y(t)\)をインパルス応答とよびます。
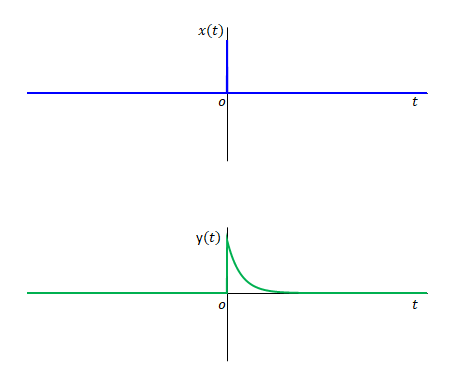
この応答の例は電気回路の「RC直列回路」に相当します。\(x(t)\)が電源に生じた電圧とすると、コンデンサに生じる電圧が\(y(t)\)です。
※図では\(x(0)\)を有限の値として描いていますが、ディラックのデルタ関数なので実際は無限大です。
1.2 \(t=0\)以外でインパルスが発生する場合
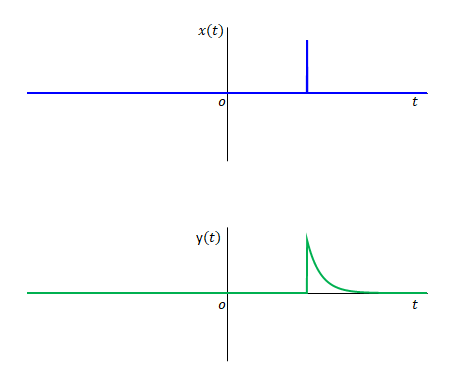
インパルス応答は\(t=0\)で\(x(t)\)インパルスが発生する場合の\(y(t)\)です。では\(t=0\)以外でインパルスが発生する場合、\(y(t)\)はどう違うでしょう。
これはシステムによります。遅れてパルスが発生すると\(y(t)\)の大きさが変わるかもしれないし、グラフに表示したときの波形が変わっているかもしれません。
しかし、パルスの位置に関わらず\(x(t)\)と\(y(t)\)の時間関係は一定で\(y(t)\)の大きさ・波形も変わらないシステムもあるもしれません。
このような性質を「時不変」とよびます。以下、時不変であった場合について考えます。
2 畳み込み
2.1 複数のインパルスが発生する場合
次に\(x(t)\)に複数のインパルスが発生する場合を考えます。
\(y(t)\)はそれぞれのインパルスの応答が足し合わされます。
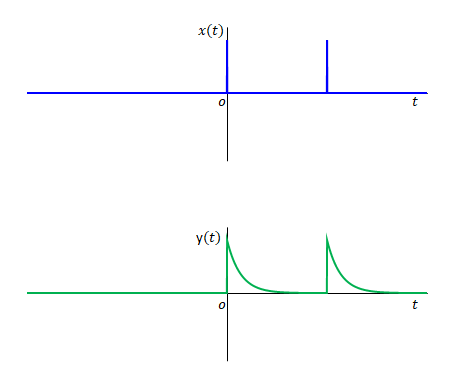
ただし、これは\(g(x)\)が「線形」であった場合の性質です。つまり「重ね合わせの原理」が成立する状態です。これらについては「フーリエ変換1」の3章で簡単に述べています。
線形と時不変を合わせ「線形時不変系システム」とよびます。
2.2 無数のインパルスが発生する場合
\(x(t)\)のインパルスの数を増やしてゆき隙間がない状態になったとしたらどうなるでしょう。それぞれのインパルスの大きさが同じで、ある区間内のみ存在するとすれば、矩形関数になりますね。
矩形関数と同時に表示される\(y(t)\)が矩形関数への応答ということになります。
2.3 畳み込み
前項まで、時不変システムでは\(x(t)\)をインパルスの集まりと考えて、\(y(t)\)をインパルス応答の重ね合わせとして求めることができることを述べました。
次にこれを式で表した場合について考えてみましょう。
その式が以下です。
$$y(t)=\int^{\infty}_{-\infty} x(\tau)g(t – \tau) d\tau$$
右辺に\(\tau\)という変数が登場しました。右辺は\(\tau\)で積分しているので、積分後は\(\tau\)が消えて\(t\)だけの関数になります。
これは「畳み込み(畳み込み積分)」とよばれます。
一方の関数を平行移動させながら両者の積の求め、さらに積分を求める演算です。
次節以降でこの式の意味を述べます。
※畳み込みは\(\ast\)を使い以下のように表すことがあります。
$$y(t) = x(t) \ast g(t) $$
2.4 畳み込みのグラフ表示
畳み込みの定義に従って動的なグラフを表示します。次項以降で補足します。
以下、グラフの説明です。
表示
・上段のグラフは\(x(\tau)\)(青色)と\(g(t-\tau)\)(赤色)を重ね合わせています。
・中段(紫色)はその積です。
・下段は(緑色)は\(y(t)\)です。
操作
・「開/止」ボタンを押すと表示更新と停止を交互に切り替えます。
・「速」ボタンを押すと3段階で速さを切り替えます。
・「x」ボタンを押すごとに\(x\)を以下のように切り替えます。
インパルス(1本)→インパルス(2本)→インパルス(10本)→インパルス(20本)→矩形→三角
・「g」ボタンを押すごとに\(g\)を以下のように切り替えます。
微分回路→矩形→積分回路→インパルス
※微分回路とは電気回路のRC直列回路における電源と抵抗の電圧の関係です。
積分回路は電源とコンデンサの電圧の関係です。
微分・積分に近い性質をもちますが、数学における微分とは異なります。
次章で補足します。
3 畳み込みに関する疑問
3.1 なぜ\(g\)が反転している?
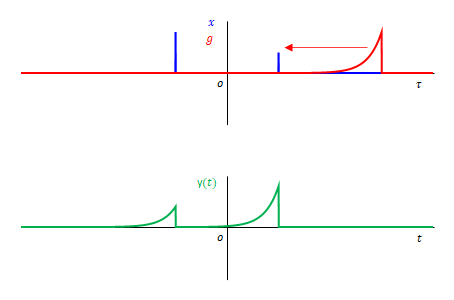
上図は\(g(t-\tau)\)を右へ移動させています。しかし、赤のグラフをよく見てください。左右を反転させています。ある時刻に急に立ち上がり、緩やかに下がる関数のはずですが、その逆になっています。
しかし緑色の\(y(t)\)は意図した波形になっています。 \(x\)がインパルスなので\(g\) と\(y(t)\)は同じ波形になります。つまり\(g\)もこうなるはずです。 何が異なるのでしょう。
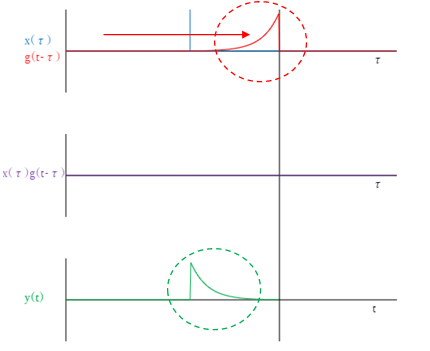
まず注意していただきたいのは、グラフ上段と中段の横軸は\(t\)ではなく\(\tau\)であるという点です。前項のグラフ上の時間経過とともに変化するのは\(\tau\)ではなく\(t\)です。上段から下段まで貫いている縦棒が\(t\)を示しています。
畳み込みの式は、全ての瞬間で中段の値を\(\tau\)で積分していることを示しています。
さて、\(g\)を反転させる理由をグラフで考えます。
\(g\)を反転させた場合とさせなかった場合を比較します。
また、\(g\)は\(t\)の経過とともに左から右へ移動しますが、右から左へ移動させた場合とも比較します。以下(a)から(d)の4通りです。
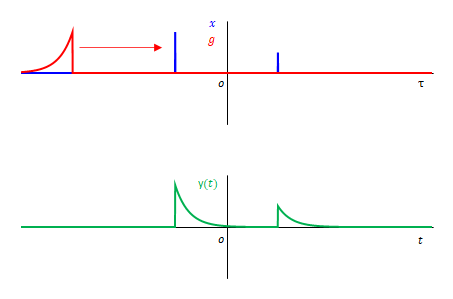
(a) \(g\)を反転させ、左から右へ移動
\(g\)は畳み込みの定義通りです。\(y(t)\)は正しく表示されます。
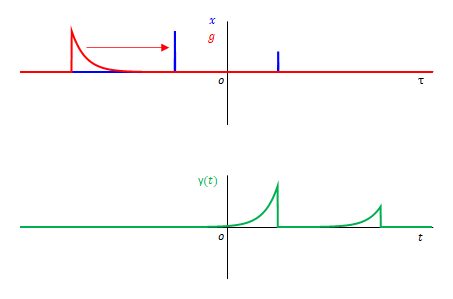
(b) \(g\)を反転させず、左から右へ移動
\(g\)の向きが畳み込みと定義とは逆です。\(y(t)\)は正しく表示されません。
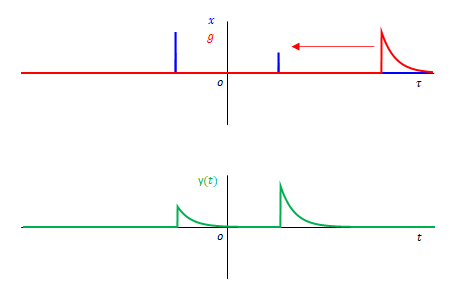
(c) \(g\)を反転させず、右から左へ移動
\(g\)の移動方向が畳み込みの定義とは逆です。それぞれのインパルスに対する応答は正しそうですが、両者の関係が逆になっています。\(y(t)\)は左側に大きい波形がなければならないのにそうはなっていません。
(d) \(g\)を反転させ、右から左へ移動
\(g\)の向きと移動方向が逆です。これも\(y(t)\)は正しくありません。
以上、正しいのは(a)だけでした。やはり\(g\)は反転させる必要があります。また、\(t\)の経過とともに左から右へ移動する必要もあります。
このことが畳み込みの式の\(g\)と一致するか確認しましょう。
畳み込みの式は以下でした。
$$y(t)=\int^{\infty}_{-\infty} x(\tau)g(t - \tau) d\tau$$
\(t\)が増えるにつれて\(g\)が移動するので関数の括弧の中には\(t\)が入ります。
\(\tau\)軸上で\(g\)がインパルス応答を描かないといけないので括弧の中には\(\tau\)も入ります。ただし左右が反転するので負の符号がつきます。
したがって \(g(t-\tau)\) でなければならないのです。
3.2 グラフ中段と下段の関係がわかりづらい
次に中段のグラフと下段のグラフの関係についてです。
その前に上段と中段の関係についてです。
中段は\(x(\tau)\)と\(g(t-\tau)\)の積です。これはそれぞれの\(\tau\)における積を表示しています。そして、上段から下段に貫いている縦棒が左から右へ移動するにつれて上段と中段を更新しています。これはわかりやすいでしょう。
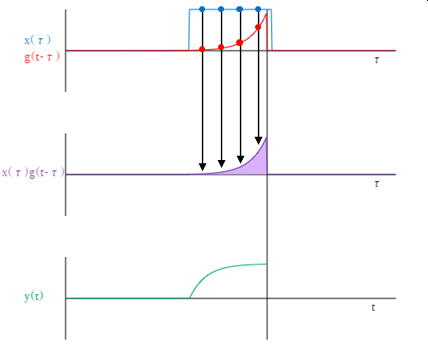
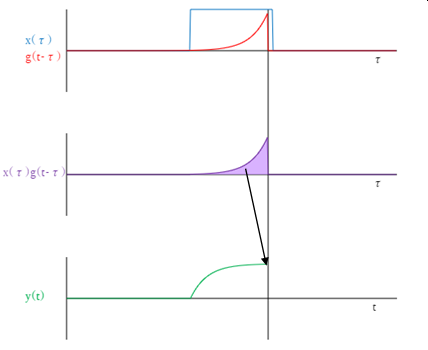
しかし下段の横軸は\(\tau\)ではなく\(t\)です。上段・中段と違う変数を並べて表示しているのでわかりづらいかもしれません。
また、\(y(t)\)は中段の\(x(t)g(t-\tau)\)の面積を示しています。しかもそれは縦棒が示す1点に反映されます。それより右はまだ値が決まらず、左は既に値が確定しています。
3.3 なぜ\(x(t)\)ではなく\(x(\tau)\)?
見過ごしてしまいそうですが、上段の\(x\)の括弧の中は\(t\)ではなく\(\tau\)の関数です。
\(t\)ではだめなのでしょうか。
畳み込みは、ある\(t\)における\(x\)と\(g\)の乗算の積分を求める演算です。\(\tau\)とともに\(x\)と\(g\)が連動しなければなりません。もし括弧の中が\(\tau\)ではなく\(t\)であった場合、\(\tau\)を変えても\(x\)は変わりません。したがって\(x(\tau)\)にする必要があります。
3.4 なぜ伝達関数を使う場合は畳み込みをしなくてもよい?
「フーリエ変換6(周波数伝達関数)」を思い出してください。\(x(t)\)から\(y(t)\)を求めるためにフーリエ変換をし、伝達関数を掛け、フーリエ逆変換をしました。下図のオレンジ色の経路です。
しかしフーリエ変換を使わなくても時間領域の演算で\(y(t)\)を求められます。それが茶色の経路です。本ページで述べたのはこの経路です。また、\(g(t)\)と\(G(\omega)\)も片方がわかればフーリエ変換・フーリエ逆変換でもう一方を求めることができます。
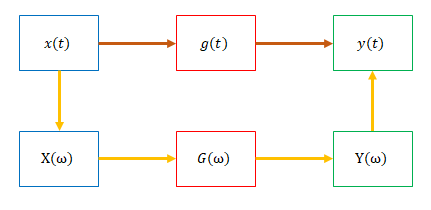
\(x(t)\)から\(y(t)\)を得られることには違いがありませんが、\(x(t)\)から\(y(t)\)を求める演算方法と\(X(\omega)\)から\(Y(\omega)\)を求める演算方法には大きな違いがあります。
式にすると以下です。
$$y(t) = x(t) \ast g(t) $$
$$Y(\omega) = X(\omega) G(\omega)$$
角周波数領域で伝達関数を使う場合は角周波数ごとに\(X(\omega)\)と\(G(\omega)\)を掛け\(Y(\omega)\)とすればよいだけでした。
しかし時間領域ではそういういわけにはいきません。畳み込みが必要です。
なぜでしょう。
線形時不変システムにおいては 角周波数領域では\(Y(\omega)\)は同一角周波数の\(X(\omega)\)と\(G(\omega)\)のみに影響を受けるので畳み込みは必要ありません。単にそれぞれの角周波数で乗算をするだけですみます。
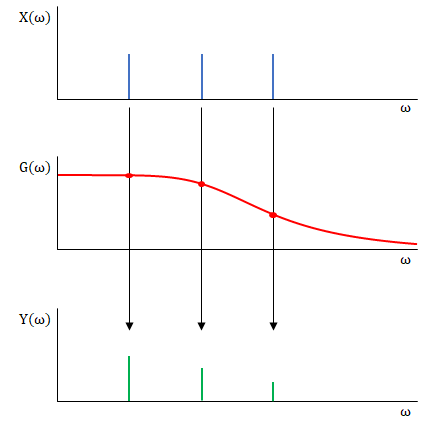
しかし時間領域で演算する場合は異なります。図のように\(x(t)\)がインパルスであるにもかかわらず\(y(t)\)は時間方向に無限に広がっているからです。特定の時間における値の乗算のみで求めることはできません。

実用においてインパルス応答を使わず伝達関数を使うことがあるのは、畳み込みをしなくてもよいという利点があるからでしょう。
4 まとめ
・時間0のみでインパルスが発生している入力に対する出力をインパルス応答とよびます。
・入力を平行移動させた(入力全体を早めたまたは遅らせた)場合にその移動分だけ出力も平行移動する(大きさなどが変わらない)性質を「時不変」とよびます。
・入力を複数の関数に分解し、それぞれの出力を求め、それらの総和を求めることにより分解前の入力の応答が得られる場合、この性質を「線形」とよびます。
・インパルス応答のわかっている線形時不変システムでは、入力をインパルスに分解し、それぞれのインパルス応答を重ね合わせることにより出力を得ることができます。
・前項の出力は以下の操作によって求めることができます。
$$y(t)=\int^{\infty}_{-\infty} x(\tau)g(t - \tau) d\tau$$
これは「畳み込み」とよばれる演算です。
