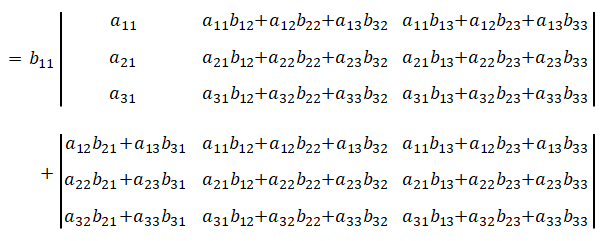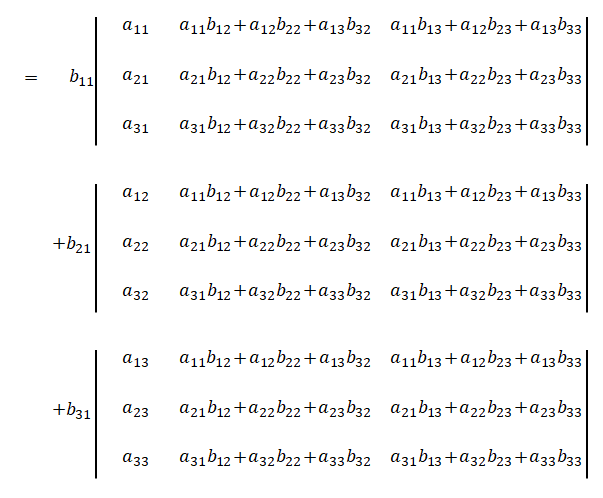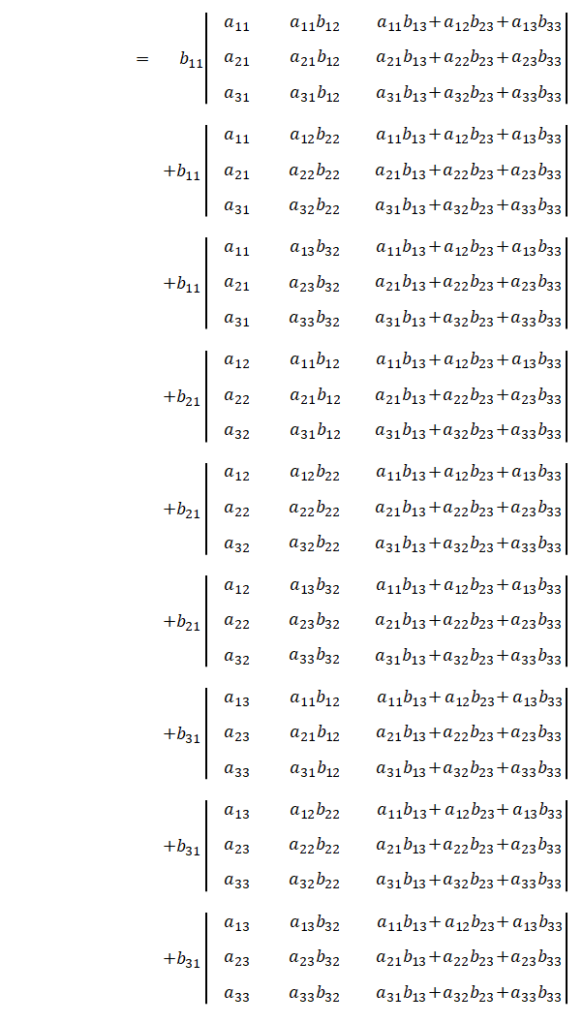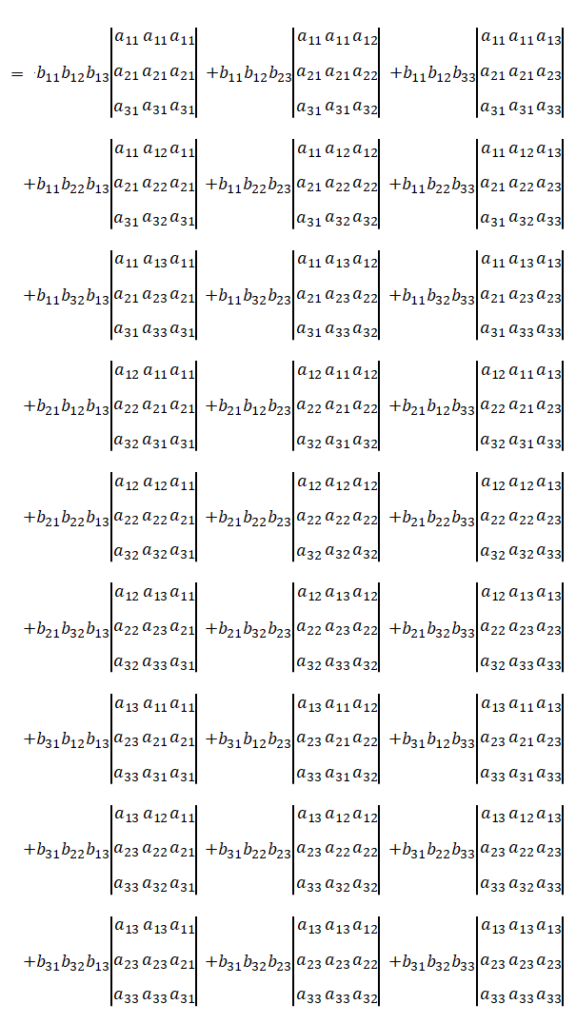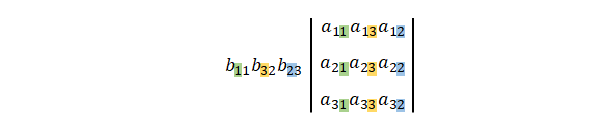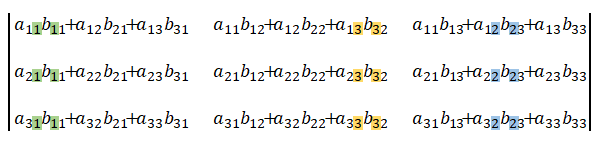定理
\(2\)つの行列の積の行列式は、それぞれの行列の行列式の積に等しい。
$$\mathrm{det}(AB)=\mathrm{det}(A)\mathrm{det}(B)$$
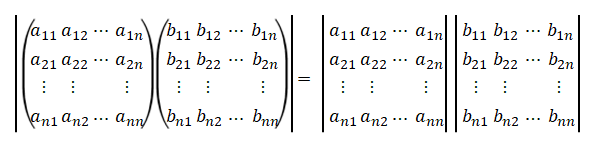
証明1
以下のように\(A\)を基本行列の積により表す。
$$A = E_{k}E_{k-1}\cdots E_{1}$$
基本行列と任意の正方行列の積の行列式はそれぞれの行列式の積と等しいので、
\begin{align}
\mathrm{det}(AB)&=\mathrm{det}(E_{k}E_{k-1}\cdots E_{1}B)\\
&=\mathrm{det}(E_{k})\mathrm{det}(E_{k-1})\cdots\mathrm{det}(E_{1})\mathrm{det}(B)\\
&=\mathrm{det}(A)\mathrm{det}(B)
\end{align}
■
証明2
\(A\)に対する行基本変形、\(B\)に対する列基本変形の組み合わせにより以下のように上三角行列\(EA\)、\(BF\)が得られたとする。
\begin{align}
E_{k}E_{k-1}\cdots E_{1} A &= EA\\
B F_{1}F_{2}\cdots F_{p} &= BF\\
\end{align}
\(EABF\)、\(EA\)、\(BF\)に関し以下のことがいえる。
・\(EABF\)は上三角行列である。
・\(EABF\)の対角成分の積は\(EA\)と\(BF\)の対角成分の積と等しい。
・上三角行列の対角成分の積は行列式と等しい。
以上より、
$$\mathrm{det}(EABF)=\mathrm{det}(EA)\mathrm{det}(EB)$$
左辺と右辺の行列式を以下のように分ける。
\begin{align}
\mathrm{det}(EABF)&=\mathrm{det}(E)\mathrm{det}(AB)\mathrm{det}(F)\\
\mathrm{det}(EA)\mathrm{det}(BF)&=\mathrm{det}(E)\mathrm{det}(A)\mathrm{det}(B)\mathrm{det}(F)
\end{align}
したがって、
$$\mathrm{det}(AB)=\mathrm{det}(A)\mathrm{det}(B)$$
■
補足
\(A\)、\(B\)を以下のように定義します。
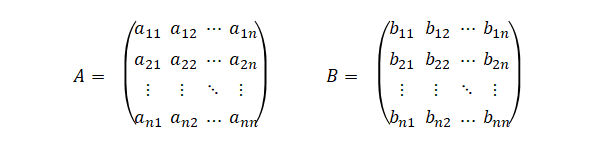
\(A\)に対する行基本変形の組み合わせ、\(B\)に対する列基本変形の組み合わせによりそれぞれ上三角行列に変形したとします。
行基本変形は左から、列基本変形は右から基本行列を掛けることと同じなので、三角行列を、
\begin{align}
E_{k} E_{k-1} \cdots E_{1} A&=E A\\
B F_{1} F_{2} \cdots F_{p}&=B F\\
\end{align}
と定義します。

\(2\)つの上三角行列の積も上三角形なので、\(AB\)の左から\(E\)、右から\(F\)を掛けた行列も上三角行列です。
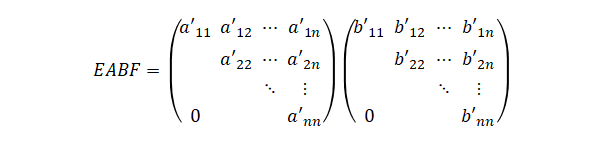
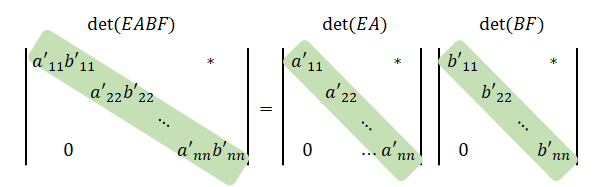
また、上三角行列の積の対角成分は、それぞれの行列の対角成分の積なので、\(EABF\)の対角成分の積は\(EA\)の対角成分と\(BF\)の対角成分の積と等しくなります。
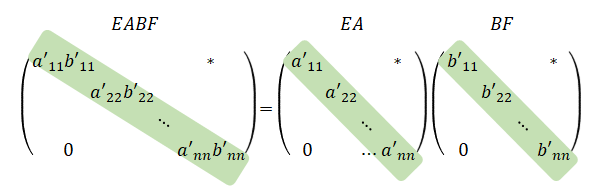
さらに、上三角行列の行列式は対角成分の積と等しくなります。
したがって、
\begin{align}
\mathrm{det}(EABF)&=a^{\prime}_{11}b^{\prime}_{11}a^{\prime}_{22}b^{\prime}_{22}\cdots a^{\prime}_{nn}b^{\prime}_{nn}\\
\end{align}
\begin{align}
\mathrm{det}(EA)\mathrm{det}(BF)&=a^{\prime}_{11}a^{\prime}_{22}\cdots a^{\prime}_{nn}b^{\prime}_{11}b^{\prime}_{22}\cdots b^{\prime}_{nn}\\
\end{align}
より、
$$\mathrm{det}(EABF)=\mathrm{det}(EA)\mathrm{det}(BF)$$
基本行列と、任意の同じサイズの正方行列の積の行列式は、それぞれの行列式の積と等しいので、
$$\mathrm{det}(EABF)=\mathrm{det}(E)\mathrm{det}(ABF)=\mathrm{det}(E)\mathrm{det}(AB)\mathrm{det}(F)$$
$$\mathrm{det}(EA)\mathrm{det}(BF)=\mathrm{det}(E)\mathrm{det}(A)\mathrm{det}(B)\mathrm{det}(F)$$
上の\(2\)式は等しいので、それぞれの右辺を\(\mathrm{det}(E)\mathrm{det}(F)\)で割ると、
$$\mathrm{det}(AB)=\mathrm{det}(A)\mathrm{det}(B)$$
となります。
証明3
以下のように定義する。
$$A=(a)_{ij},B=(b)_{ij}\ \ \ (i,j=1,2,\cdots,n)$$
$$A=(\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots \boldsymbol{a}_n)$$
積の行列は、
$$AB=\left(\sum_{i_1=1}^n a_{1\,i_1 }b_{i_1\,1} , \sum_{i_2=1}^n a_{2\,i_2 }b_{i_2\,2} , \cdots \sum_{i_n=1}^n a_{n\,i_n }b_{i_n\,n} \right)$$
行列式は、
\begin{align}
\mathrm{det}(AB)&=\mathrm{det}\left(\sum_{i_1=1}^n a_{1\,i_1 }b_{i_1\,1} , \sum_{i_2=1}^n a_{2\,i_2 }b_{i_2\,2} , \cdots \sum_{i_n=1}^n a_{n\,i_n }b_{i_n\,n} \right)
\end{align}
多重線形性により\(B\)の成分を行列式の外に出し、さらに同一の列を含む行列式を削除し、
\begin{align}
{\mathrm{det}(AB)}&=\sum_{\sigma \in S_n} b_{\sigma(1)1} b_{\sigma(2)2} \cdots b_{\sigma(n)n}
\mathrm{det}\left(\boldsymbol{a}_{\sigma(1)}, \boldsymbol{a}_{\sigma(2)}, \cdots \boldsymbol{a}_{\sigma(n)} \right)
\end{align}
行列式内の列と\(B\)の成分を並べ替え、
\begin{align}
{\mathrm{det}(AB)}&=\sum_{\sigma \in S_n} b_{\sigma(1)1} b_{\sigma(2)2} \cdots b_{\sigma(n)n} \mathrm{sgn}(\sigma^{-1})
\mathrm{det}(\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots \boldsymbol{a}_n )\\
&=\sum_{\sigma^{-1} \in S_n} \mathrm{sgn}(\sigma^{-1}) b_{1\sigma^{-1}(1)} b_{2 \sigma^{-1}(2)} \cdots b_{n\sigma^{-1}(n)}
\mathrm{det}(\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots \boldsymbol{a}_n )\\
&=\mathrm{det}(A)\mathrm{det}(B)
\end{align}
■
補足
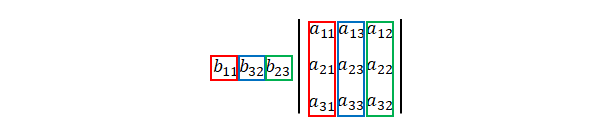
以下の\(3\times 3\)の行列について考えます。
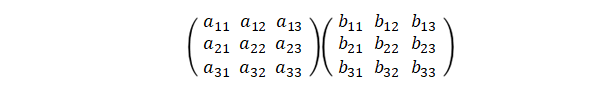
積は、
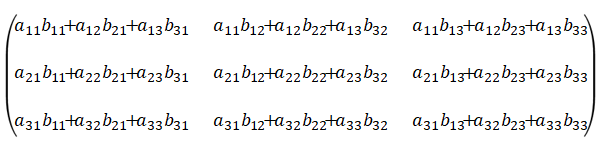
行列式は、
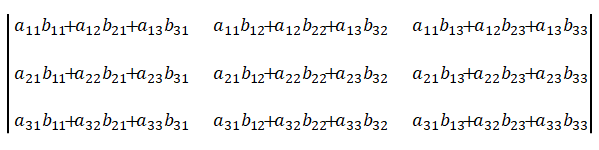
と表されます。
多重線形性により、各列にある\(3\)の項の全ての組み合わせ、つまり\(27\)個の行列式に分けます。

しかし全ての項に意味があるわけではありません。\(2\)つの列が同じである行列の行列式は\(0\)なので除外すると、
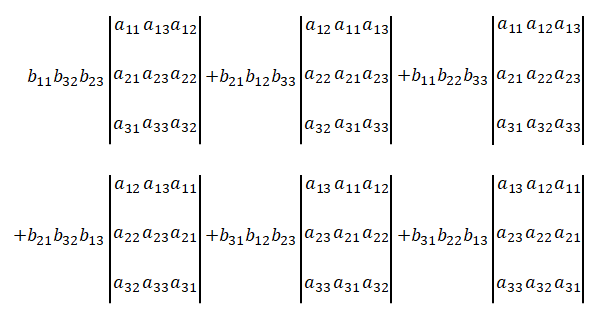
\(6\)個の項のみになります。
置換を使って以下のように表します。
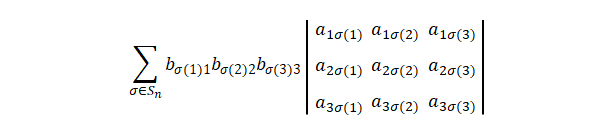
\(A\)の列を左から昇順に並べ替えます。並べ替え前の列の並びが\(\sigma\)で表されるので、並べ替えの変形は\(\sigma^{-1}\)です。列の交代性により符号が変わるので、\(\mathrm{sgn}(\sigma^{-1})\)が付きます。
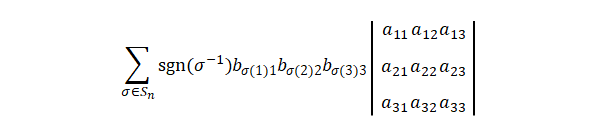
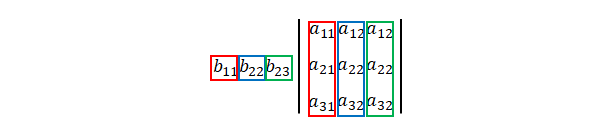
\(B\)の成分の行と列を変形します。この時点では列と行は以下の対応になっています。
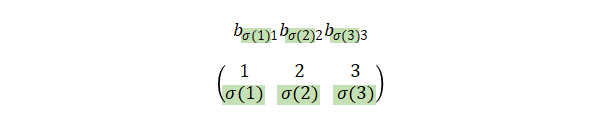
列\(1\)、\(2\)、\(3\)は行\(\sigma(1)\)、\(\sigma(2)\)、\(\sigma(3)\)を逆置換したと考えられるので、
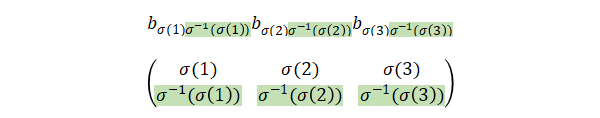
行が昇順となるよう並べ替えます。\(\sigma(1)\rightarrow 1\)、\(\sigma(2)\rightarrow 2\)、\(\sigma(3)\rightarrow 3\)と置き換えたと考えると、
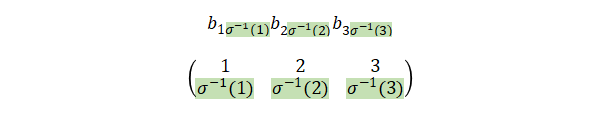
したがって、
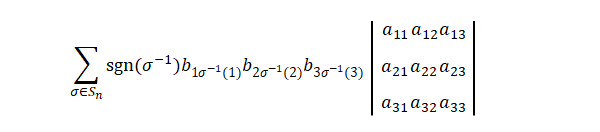
\(\sigma\)に\(-1\)がついていますが、たとえば\(\tau\)などに置き換えれば、式の左側は\(B\)の行列式であることがわかります。以上より、
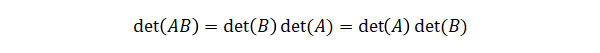
となることが確認できました。