定義
以下のように行と列を入れ替えた行列を転置行列とよび、\(A^T\)のように表す。
下の図は対角を軸として反転するところのイメージです。
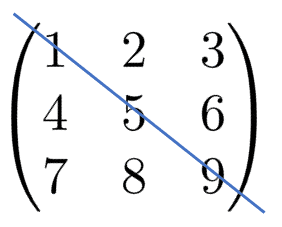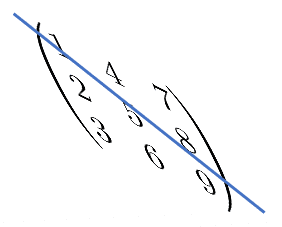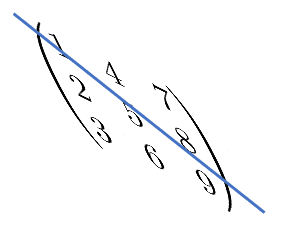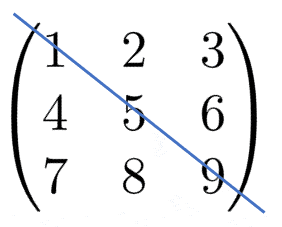
例
定理
\begin{align} &1.\ \ (A^{T})^T=A\\ &2.\ \ (A+B)^{T}=A^T+B^T\\ &3.\ \ (cA)^{T}=cA^T\\ &4.\ \ \mathrm{det}(A^{T})=\mathrm{det}(A)\\ &5.\ \ (AB)^{T}=B^TA^T\\ &6.\ \ (A^{T})^{-1}=(A^{-1})^T\\ &7.\ \ \langle A , B \rangle =\mathrm{tr}(A^TB) \end{align}
\(1.\ – \ 3.\ \)の証明は省略します。
\(4.\ \ \mathrm{det}(A^{T})=\mathrm{det}(A) \)の証明
行列式の転置不変性参照。
\(5.\ \ (AB)^{T}=B^TA^T\)の証明
\(A\)の\((i,j)\)成分を\(A_{ij}\)のように表す。
\begin{align}
((AB)^T)_{ij}&=(AB)_{ji}\\&=\sum_{k=1}^n A_{jk} B_{ki} \\&= \sum_{k=1}^n B_{ki} A_{jk}\\& = \sum_{k=1}^n (B^T)_{ik} (A^T)_{kj}
\end{align}
したがって\((AB)^T=B^T A^T\)が成り立つ。
■
補足
例として、\((AB)^T\)の\((2,1)\)成分に注目します。
これは\(AB\)の\((1,2)\)成分でもあるので、図の緑色と青色の成分の積和です。
一方、\(B^TA^T\)の\((2,1)\)成分は\(B\)の第\(2\)行、\(A\)の第\(1\)列の内積なので両者が等しいことがわかります。
他も同様です。
\(6.\ \ (A^{T})^{-1}=(A^{-1})^T\)の証明
$$I=I^T=(AA^{-1})^T=(A^{-1})^T A^T $$
より\(A^T\)の逆行列は\((A^{-1})^T\)であるので、
$$(A^{T})^{-1}=(A^{-1})^T$$
■
\(7.\ \ \langle A , B \rangle =\mathrm{tr}(A^TB)\)の証明
\begin{align}
\langle A,B \rangle = \sum_{k=1}^n \sum_{i=1}^n a_{ki} b_{ki} = \mathrm{tr}(A^T B )
\end{align}
■
補足
\( \langle \rangle\)は内積を表します。行列どうしの内積は各成分の積和と定義されます。
\(\mathrm{tr}\)はトレースの意味で、対角成分の和を示します。
まず\(\langle A,B \rangle\)のうち第\(1\)列の分のみに注目します。
緑と青を順に掛けて和を求めると、
$$a_{11}b_{11}+a_{21}b_{21}+a_{31}b_{31}+a_{41}b_{41}$$
次に\(\mathrm{tr}(A^T B ) \)の\((1,1)\)成分のみに注目します。
同様に積和は、
$$a_{11}b_{11}+a_{21}b_{21}+a_{31}b_{31}+a_{41}b_{41}$$
したがって内積とトレースは、
\begin{align}
\langle A,B \rangle
=&\color{white}{+} a_{11}b_{11}+a_{21}b_{21}+a_{31}b_{31}+a_{41}b_{41}\\
&+ a_{12}b_{12}+a_{22}b_{22}+a_{32}b_{32}+a_{42}b_{42}\\
&+ a_{13}b_{13}+a_{23}b_{23}+a_{33}b_{33}+a_{43}b_{43}\\
&+ a_{14}b_{14}+a_{24}b_{24}+a_{34}b_{34}+a_{44}b_{44}\\
=&\mathrm{tr}(A^T B )\\
\end{align}
となり、等しいことがわかります。
