特殊相対性理論12(同時性の相対性1)では、2方向に進む光が慣性系によっては時間差が生じることを確認しました。本ページではさらに別の例で同時性を考察し、理解を深めましょう。
また、同一性の相対性と因果律の関係について考察します。
1 同時性の相対性とは?
1.1 照明点灯の例
本ページでは各照明が点灯する瞬間を観測することにします。前ページでは光またはボールの進む時間を考慮に入れて比較しましたが、ここでは光が進む時間は考慮しない点に注意ください。
下の図のように、系\(S’\)に固定された3つの照明があり、それらが3回、\(S’\)から見て同時に点灯します。その色は順に紫、オレンジ、ピンクとします。
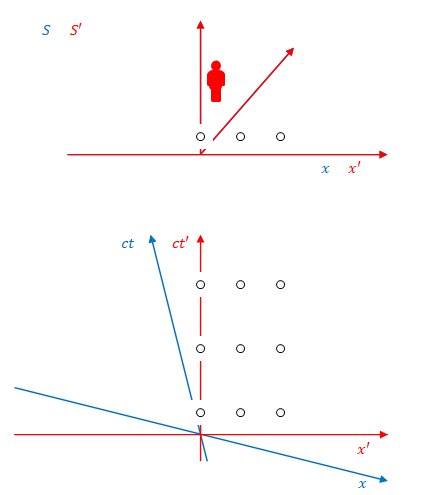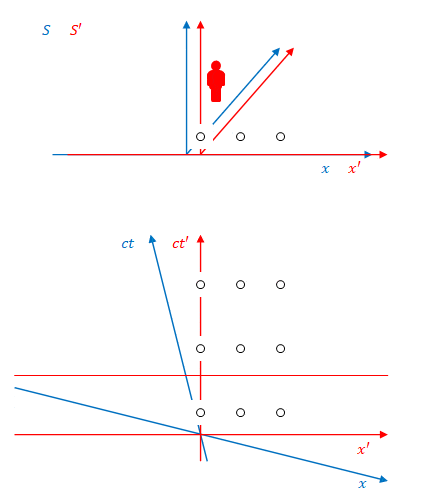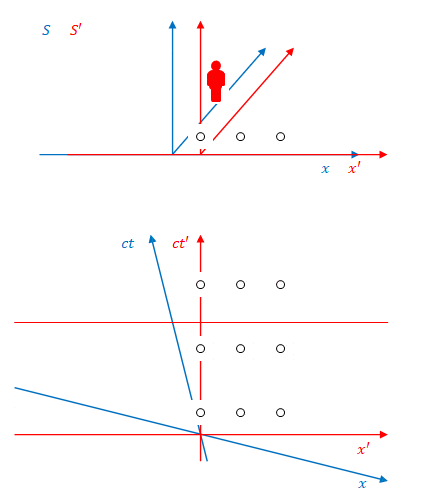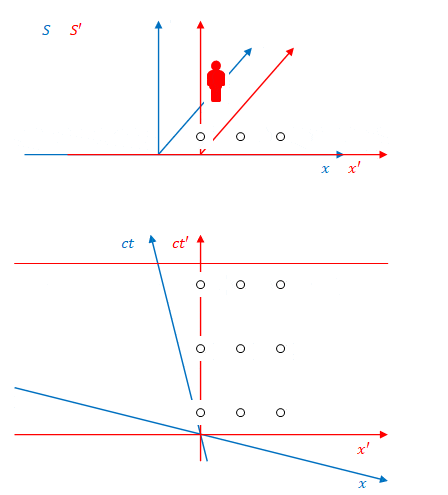
これを\(S\)から見たのが下の図です。
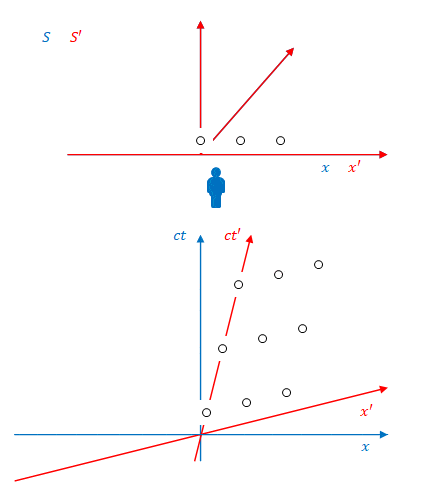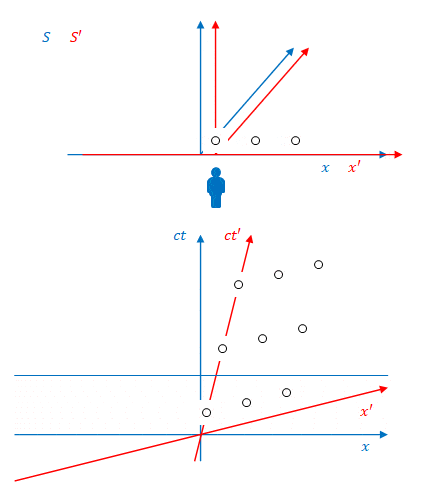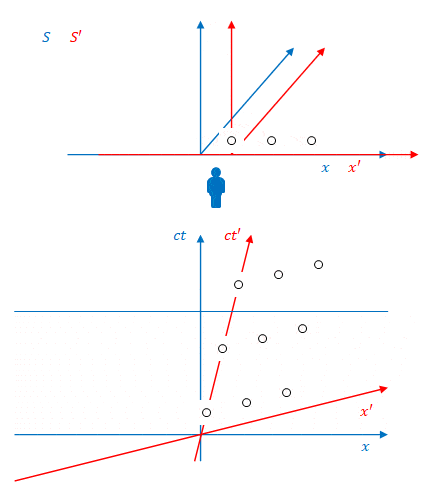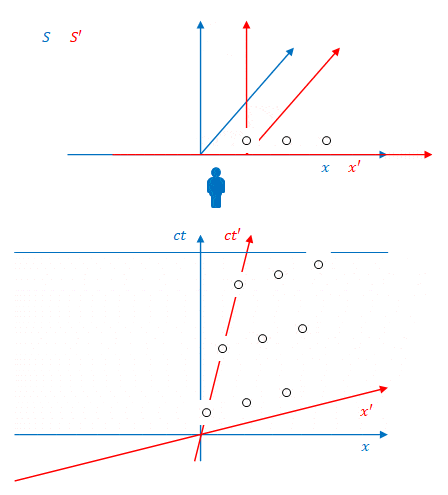
図のように、\(S\)から見ると照明は同時に点灯しません。
1.2 なぜ\(S\)から見ると同時ではない?
なぜ同時に点灯しないのでしょう。
前節のミンコフスキー図の、\(S\)から見た場合の照明の並びに注目してください。
照明は\(S’\)に固定されているので\(ct’\)軸と\(x’\)軸に平行に配置されます。
しかし、\(S\)から見ると同時刻線(ここでは同一時刻を示す線の意味)は\(x’\)軸ではなく\(x\)軸と平行です。照明は同時刻線と交わる瞬間に点灯します。したがって点灯する時刻に差が生じます。
さて、\(S\)と\(S’\)の、時間の進み方の違いについてもう少し考えてみましょう。
下の図のように、3点の事象\(A\)、\(B\)、\(C\)があります。\(S\)から見るといずれも\(ct=0\)です。
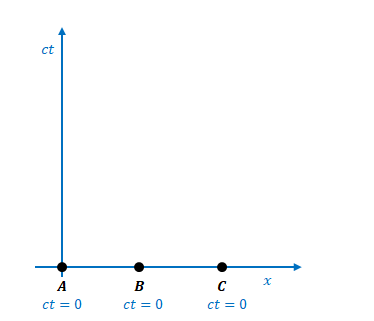
\(S’\)の座標で表すと、\(ct’=0\)、\(ct’=-0.5\)、\(ct’=-1\)と異なった時刻になります。
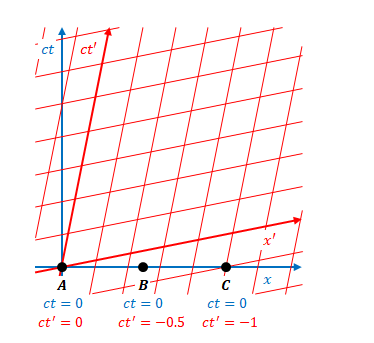
この違いは位置の違いです。原点を基準としてみるなら、原点からの距離が大きいほど時刻の差(\(ct\)と\(ct’\)の差)は大きくなります。
特殊相対性理論1(時間の遅れ、ローレンツ収縮)では、運動系の時間は遅れて見える、と述べましたが、その遅れ方は一様ではありません。
下の図のように、\(S’\)に固定された車があったとします。
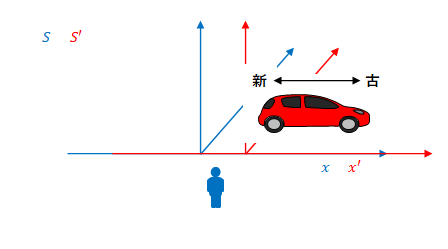
\(S\)から見ると、リアバンパー付近はより新しい像を、フロントバンパー付近はより古い像を見ているのです。
以上、同時性の相対性は、慣性系間の時刻の差が位置(空間座標)によって異なるために生じる性質です。
2 因果律
因果律とは原因と結果の関係のことです。ニュートン力学同様、特殊相対性理論においても原因と結果の時間的順序が入れ替わることはありません。同時性が相対的であるなら、因果律が破綻することはないでしょうか。つまり、慣性系によって因果関係が入れ替わることがないでしょうか。
そのことを確認します。
下の図は\(S\)の座標(時間を含む)では、事象\(A\)の後、事象\(B\)が起きていることを示しています。\(S’\)の座標においてもこの順序は変わらないことが図より読み取れると思います。
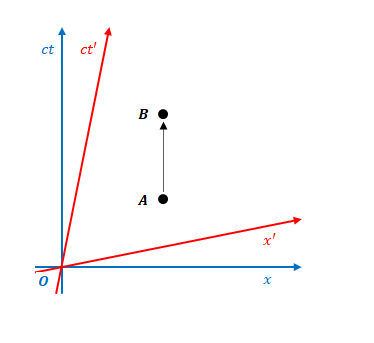
上の図は同じ位置でしたが、下の図の場合は位置が変わっています。しかし、やはり\(S\)の座標においても\(S’\)の座標においても順序は同じです。
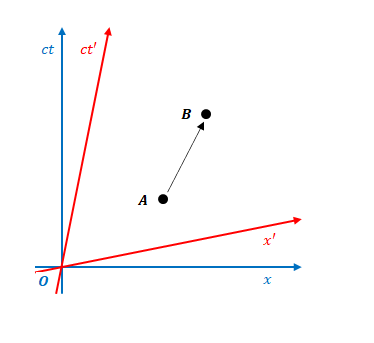
では次の例はどうでしょう。\(S\)の座標では、\(A\)が先、\(B\)が後ですが、\(S’\)の座標では\(B\)が先、\(A\)が後です。
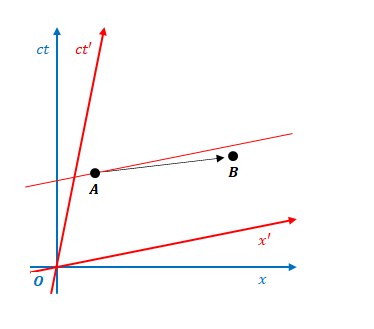
順序が入れ替わることはあるのでしょうか。
下の図は回路図です。左の2本の線は電源、\(A\)と書かれた位置にあるものはスイッチ、\(B\)と書かれた位置にあるものは照明です。
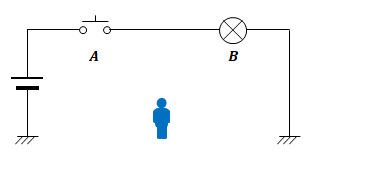
スイッチを押すと(これを事象\(A\)とします)照明が点灯します(これを事象\(B\)とします)。
さて、スイッチを押すと同時に照明は点灯するでしょうか。
スイッチと照明が離れている以上、必ず時間差があります。
その速度は最大でも光の速さです。
この例の場合は回路の電位(電場)の伝わる速さですが、やはり光速を超えることはありません。
これが電磁波でも音でも機械的な振動でも同じです。
いずれであっても照明のある位置まで伝われば何らかの方法で点灯することができるでしょう。しかし伝わらないことには点灯させることはできません。
ミンコフスキー図に戻ります。
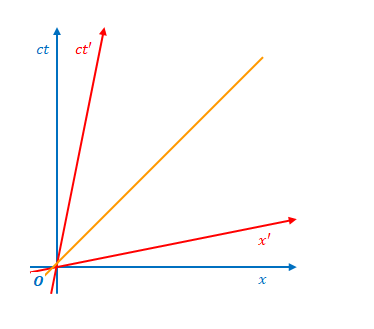
光の軌跡を図で表すと傾きは\(1\)になります(\(ct\)と\(x\)の単位長が一致している場合)。そして、ミンコフスキー図では傾きが小さいほど高速に移動することを示しています。
したがって、前述の例のような、\(A\)と\(B\)を結んだ線の傾きが\(1\)より小さくなることがそもそもありえないということです。もしそのような傾きであったとしたら、\(A\)と\(B\)には因果関係はありません。例えば、\(B\)は\(A\)とは無関係な別の回路によって点灯するのかもしれません。いずれにしても、この例をもって因果律を確認することはできません。
一方、\(x’\)軸は傾き\(1\)を超えることはありません。
したがって、もし\(S\)の座標において\(A\)→\(B\)の関係にあれば、必ず\(S’\)の座標においても\(A\)→\(B\)の関係にあります。
以上より、特殊相対性理論においては因果律が破綻することはないといえます。
3 まとめ
・慣性系間の時刻の差は位置によって異なります。その差は原点から離れるほど大きくなります。この性質により同一性が相対的になります。
・2つの事象に因果関係がある場合、その関係は光速を超えずに伝わる範囲でなければなりません。光速を超えないという制約により、因果律は常に守られます。
