双子のパラドックスは、矛盾しているようにみえるという意味ではパラドックスではありますが、実は相対性理論によって説明ができます。一般相対性理論が示す原理を用いることが最も明快なのですが、特殊相対性理論でも数通りの説明が可能です。ここではその一つについて取り上げます。
1 双子のパラドックスとは?
双子の兄弟がいます。弟は地球上にいます。兄は宇宙船で旅行をして地球へ戻ります。
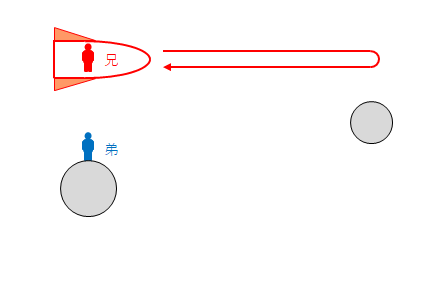
兄が戻った時、それぞれの時間はどれだけ経過しているでしょう。
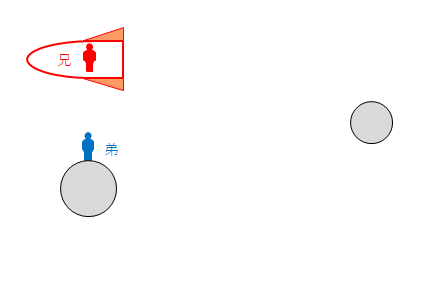
兄の飛行中に戻ります。弟から兄を見ると、兄の時間の進み方が弟のそれより遅いように見えます。
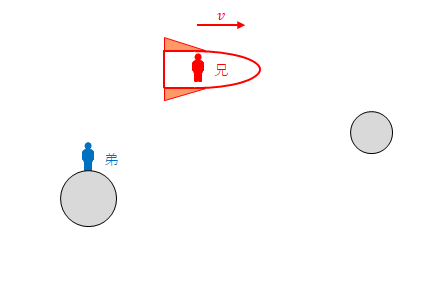
しかし兄から弟を見ると、逆に弟の時間の進み方がより遅いように見えます。
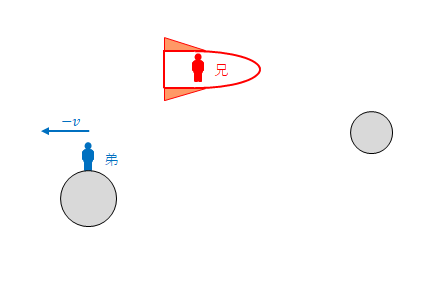
以上の2点が正しいのであれば、両者が再会したとき、両者のどちらがより年を取っていても、あるいは同じであっても矛盾するのではないか、という疑問がこのパラドックスです。
正しくは、弟の時間より兄の時間の進み方がより遅くなります。
弟から見た兄と兄から見た弟は、速度の方向が逆であるだけで他に違いはないように思えます。なぜ時間の進み方が異なるのでしょう。
2 一般相対性理論による説明
特殊相対性理論は異なる慣性系の現象の見え方について述べています。これに対し、一般相対性理論ではあらゆる座標系を扱います。つまり特殊相対性理論では加速度の影響を考慮していませんが、一般相対性理論では加速度がある場合を考慮します。
双子のパラドックスでは加速度は関係あるでしょうか。
弟は常に静止しているとすれば加速度はありません。兄は飛行中、等速直線運動をしていたとしても折り返す時点で加速度が発生します。
※もし兄の宇宙船が減速せずにいきなり方向を変えたとしたら加速度は定義できませんが、それは考えずにいくらかの有限な加速度が兄に発生したとしましょう。
加速度があるということは重力があるということです。一般相対性理論では、重力があると時間が遅れます。したがって兄の時間の進み方がより遅くなります。つまり、加速度の有無という点で兄と弟は対称ではありません。
3 特殊相対性理論による説明
3.1 ミンコフスキー図による比較
特殊相対性理論による説明には何通りかありますが、ここでは兄が折り返した時点で兄が慣性系を乗り換えるとした場合について、ミンコフスキー図で考えてみましょう。
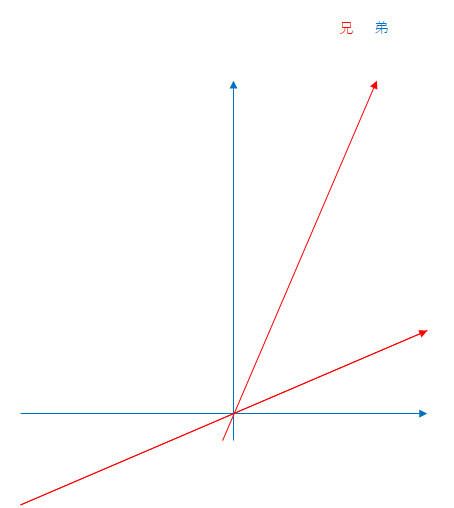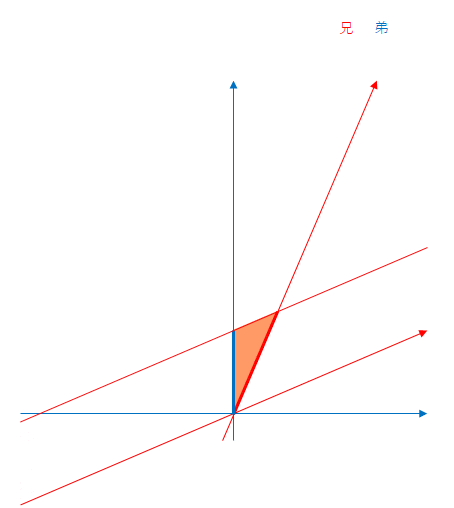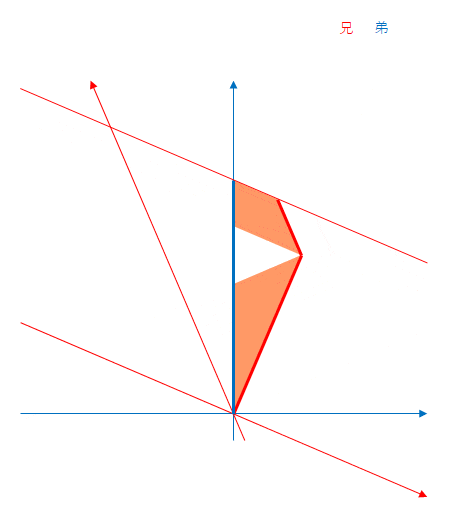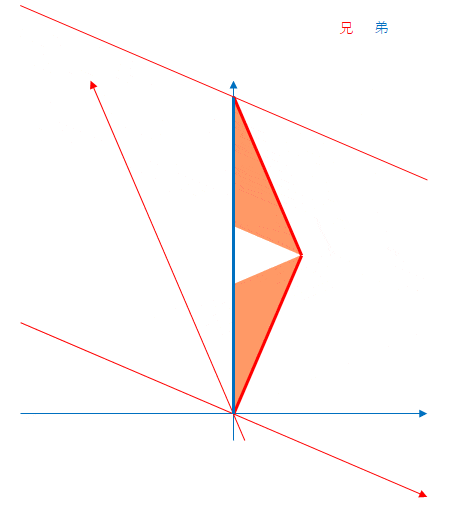
まず、弟から見た場合です。
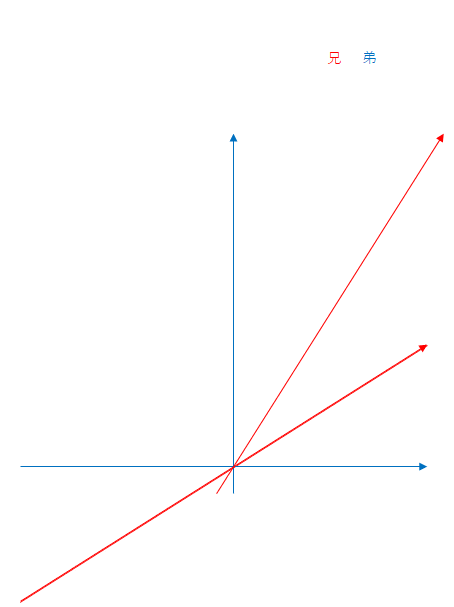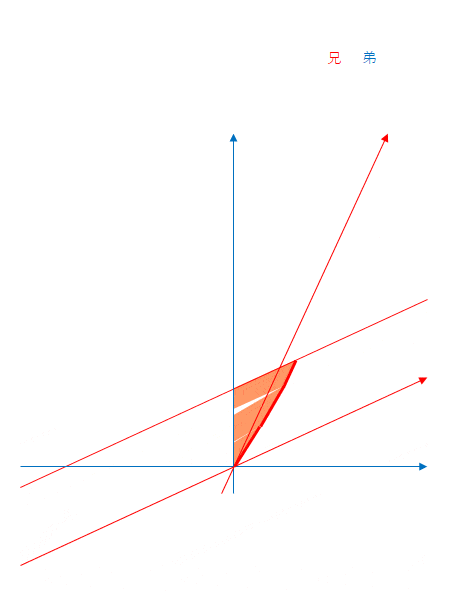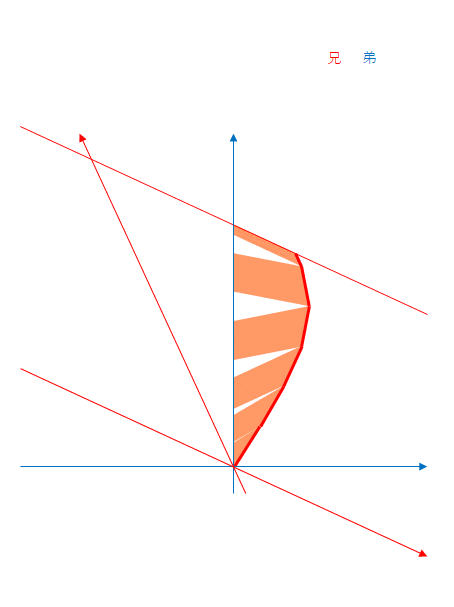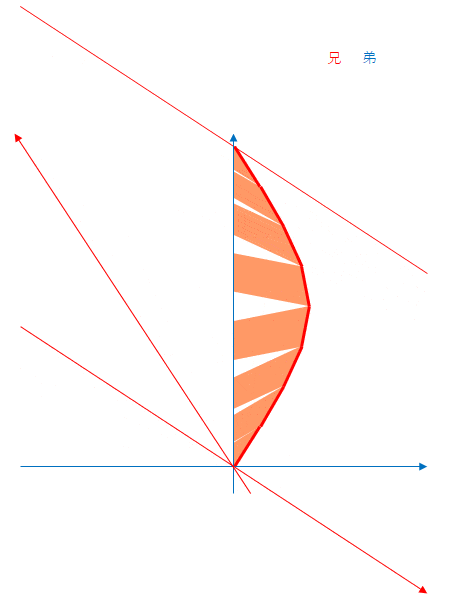
青色の矢印は弟、赤色の矢印は兄の座標軸です。兄が飛行中に折り返すと、その瞬間に兄は慣性系を乗り換えたと考えましょう。弟から見た慣性系の相対速度が変わるので、兄の座標軸は変化します。
青色と赤色の太い線は弟と兄の軌跡です。弟も兄もそれぞれの慣性形に固定されて(静止して)いるので出発後は時間軸(上向きの軸)に沿って進みます。ここでは、折り返し後に兄は原点から離れたものとしていますが軌跡は時間軸と平行に進みます。
水平な青色の動いている線は弟の時刻が同一である座標を結んだものです。ここでは同時刻線とよぶことにします。
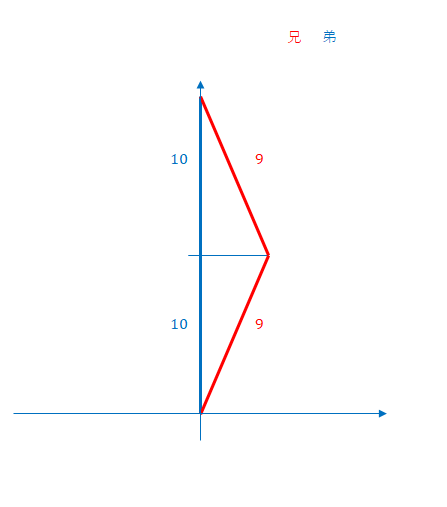
ミンコフスキー図では、線の長いほうが長い時間であるとは限りません。両者の太い線を比べると、青い線より赤い線がより長いのですが、実はこの場合は赤い線つまり兄のほうが時間はゆっくり進んでいます。
ここでは折り返し時点で弟は10年経過していたのに対し、弟から兄を見ると、9年しか経過していないとします。折り返しから帰還までの時間も同じです。
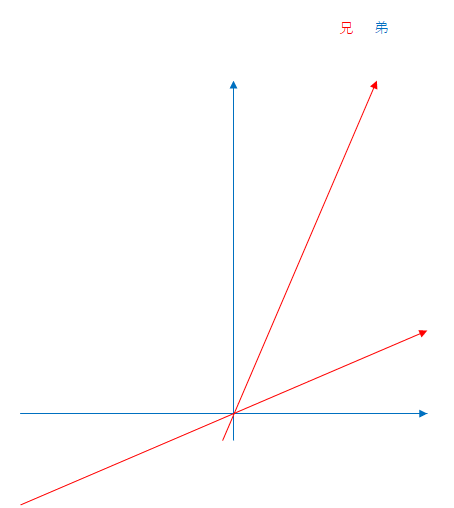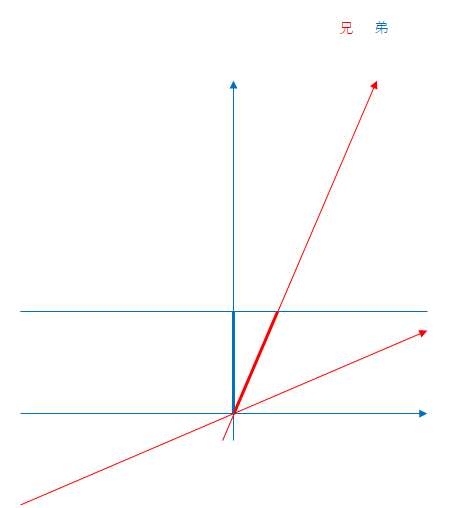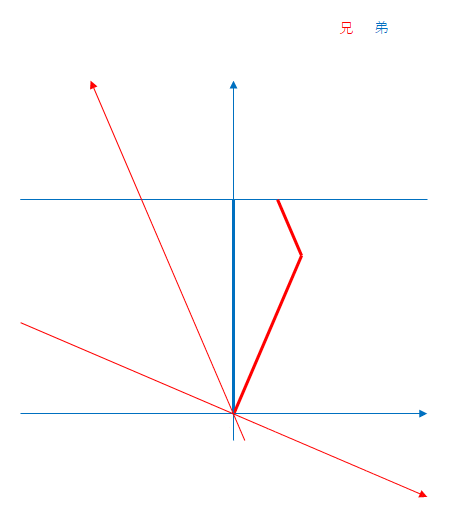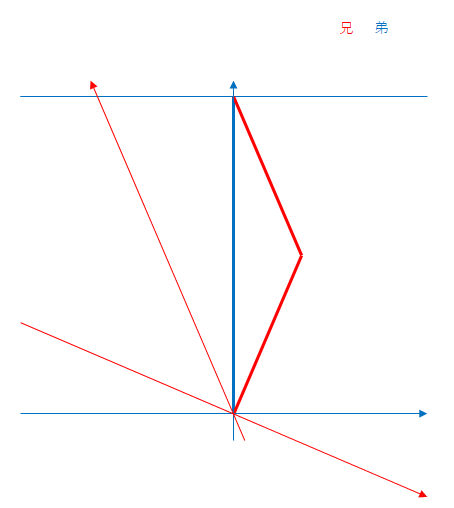
次に兄から見た場合です。
これも弟の座標軸を固定にしています。
移動する赤色の線は兄が固定されている(静止している)慣性系における同時刻線です。この線が上向きの青い軸と交わる点が弟の時間です。
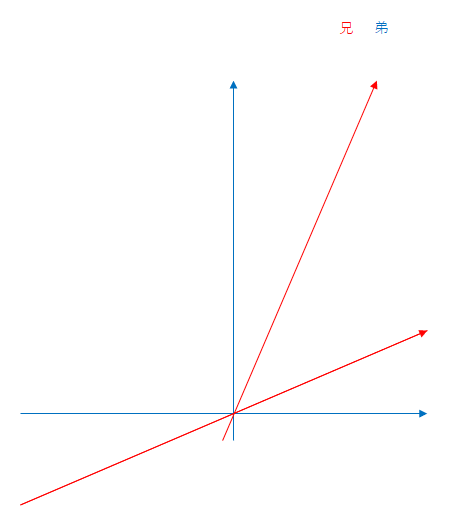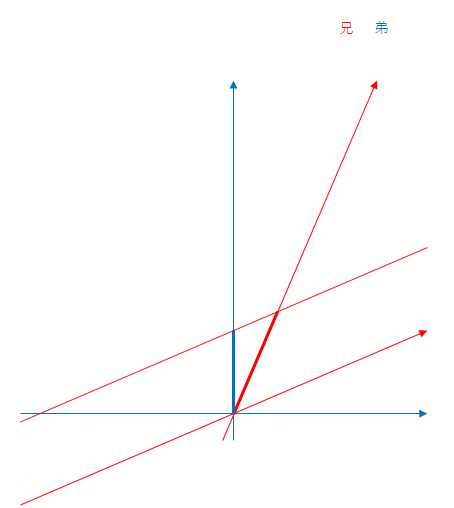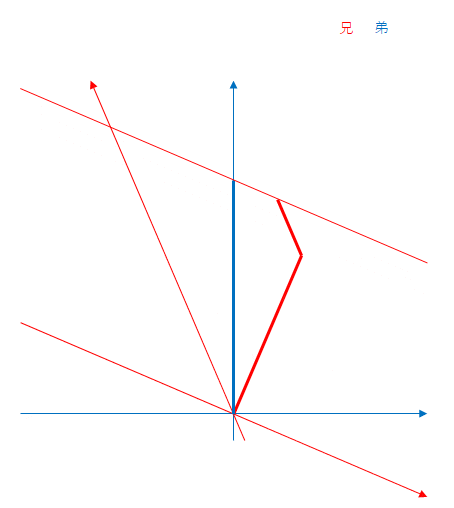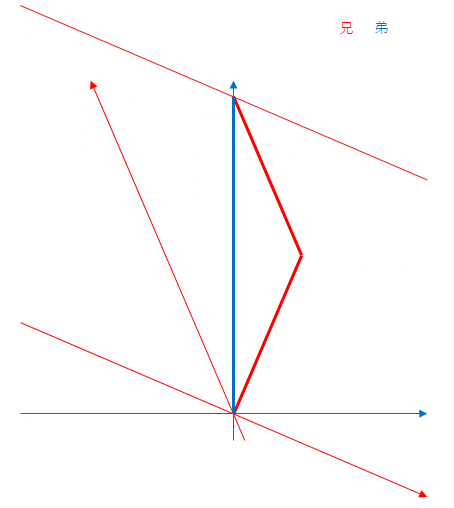
兄から見ると逆に折り返し時点で自分は10年、弟は9年しか経過していないように見えます。折り返し時点から帰還までも同じです。
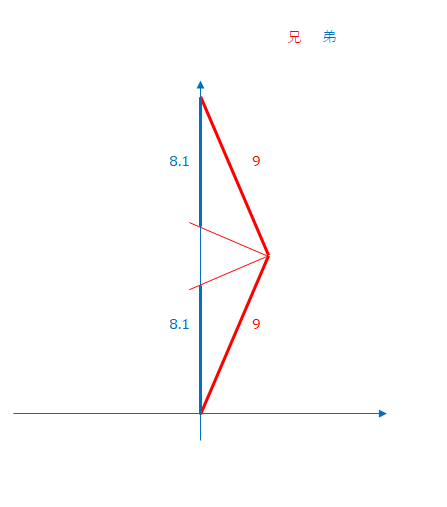
弟と兄の軌跡はミンコフスキー図では、以上のように表されます。
ではこの図ではどの部分によってパラドックスが解消されるのでしょう。
下の図の水色の部分に注目してください。兄からは、折り返した瞬間に弟の時間が急に進んだように見えます。
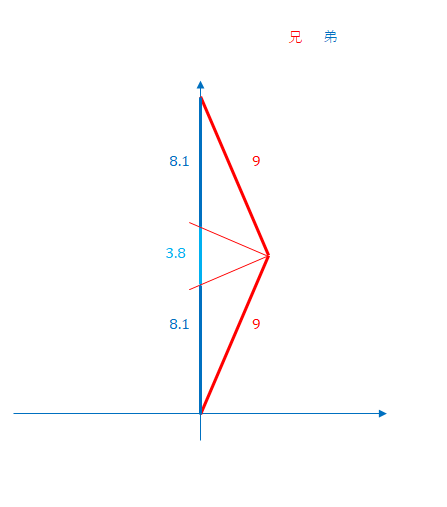
この部分によって、兄から見ても地球に帰還した時点での時間は弟のほうが進んでいるということの説明がつきます。
一般相対性理論での説明と同様、弟から見た兄と兄から見た弟は対称ではありません。その違いは、兄が慣性系を乗り換えているという点です。
では、この水色の部分がなぜ発生するのでしょう。
3.2 なぜ折り返し時に、兄から見た弟の時間が急に進む?
改めて、兄から見た場合のミンコフスキー図です。ただし、同時刻線が通ったところをオレンジ色で塗りつぶしています。
折り返したところで空白の部分が生じていますが、これは同時刻線の傾きが変わるからです。前節で述べた水色の部分です。
さて、ここまでは折り返し地点で急に兄が向きを変えるものとして考えてきましたが、そうではなくて、段階的に速度が変わる場合を考えてみましょう。
下の図の兄の軌跡は曲線にみえますが、そうではなくて折れ線です。兄は段階的に減速(後半は反対向きに加速)をしています。赤色の軸は相対速度に合わせて向きを変えています。
オレンジ色の領域は、速度が変わるたびに隙間が生じています。
つまり、速度が変わると同時刻線の傾きが変わります。これが減速であった場合、傾きは小さくなります。この同時刻線の傾きの変化によって隙間ができるのです。
この折れ線を先鋭化していくと双子のパラドックスの例と同一になるところがイメージできるのではないかと思います。
4 まとめ
・双子の兄が宇宙旅行へ出かけ、弟が地球に居続けるとします。互いに相手の時間がゆっくりと進むように見えるはずですが、そうであれば兄が地球に帰ったとき、兄の経過した時間、弟の経過した時間、どちらが長くても、あるいは同じであっても矛盾します。これが双子のパラドックスとよばれます。正しくは、兄の時間経過は、よりゆっくりになります。
・一般相対性理論によれば、このパラドックスは兄に生じる加速度によって説明できます。重力によって兄の時間の進み方が変わるからです。
・特殊相対性理論では何通りかの説明が可能です。折り返し時に兄が慣性系を乗り換えたと考えた場合、兄から見ると、折り返しの瞬間に弟の時間が急に進むために相対的に兄の時間が遅れます。
