線形代数 – グラム・シュミットの直交化法

定義

線形独立であるベクトルが張る空間の（正規）直交基底を求める方法をグラム・シュミットの直交化法とよびます。

$V$を内積空間、$\{\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_n\}$を$V$の線形独立な要素とすると、直交基底は以下により得られます。

\begin{align}
\boldsymbol{u}_1&=\boldsymbol{v}_1\\
\boldsymbol{u}_2&=\boldsymbol{v}_2-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_2 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1\\
&\ \vdots\\
\boldsymbol{u}_n&=\boldsymbol{v}_n-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_n \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1
-\cdots
-\frac{\langle \boldsymbol{u}_{n-1},\boldsymbol{v}_{n} \rangle}{\langle \boldsymbol{u}_{n-1},\boldsymbol{u}_{n-1} \rangle}\boldsymbol{u}_{n-1}
\end{align}

また、以下のように正規化すれば正規直交基底となります。

\begin{align}
\boldsymbol{e}_1&=\frac{\boldsymbol{u}_1}{\|\boldsymbol{u}_1\|}\\
\boldsymbol{e}_2&=\frac{\boldsymbol{u}_2}{\|\boldsymbol{u}_2\|}\\
&\ \vdots\\
\boldsymbol{e}_n&=\frac{\boldsymbol{u}_n}{\|\boldsymbol{u}_n\|}\\
\end{align}

グラム・シュミットの直交化法により求められたベクトルは以下を満たします。

・$\{\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_n\}$は直交集合

・$\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{n})
=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{n})$

直観的な理解（ベクトルが$2$個の場合）

上記式の通り計算すれば、$n$個の与えられたベクトルが張る空間の直交基底が得られます。また、その証明は末項に述べました。

ここでは見方を変え、ユークリッド空間に$2$個の線形独立なベクトルがあり、片方のベクトルからもう片方のベクトルへ下した垂線が、グラム・シュミットの直交化法で得られるベクトルと同一であると考えてみましょう。

線形独立なベクトル$\{\boldsymbol{v}_1,\boldsymbol{v}_2\}$があるとします。

グラム・シュミットの直交化法は以下の式で表されます。

\begin{align}
\boldsymbol{u}_1&=\boldsymbol{v}_1 \tag{1}\\
\boldsymbol{u}_2&=\boldsymbol{v}_2-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_2 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1\tag{2}\\
\end{align}

$(1)\ \boldsymbol{u}_1$

$\boldsymbol{u}_1=\boldsymbol{v}_1$とします。

$(2)\ \boldsymbol{u}_2$

$\boldsymbol{v}_2$より$\boldsymbol{u}_1$へ垂線を下ろすと、これが$\boldsymbol{u}_2$となります。

$\boldsymbol{u}_2$は$\boldsymbol{u}_1$と$\boldsymbol{v}_2$の線形結合と考えることができるので、
$$ \boldsymbol{u}_2 \in \mathrm{span}(\boldsymbol{u}_1,\boldsymbol{v}_2)$$
も満たします。

わかりやすくするために$\boldsymbol{u}_2$を移動します。図はあくまで概念を示しているだけで、移動前後で$\boldsymbol{u}_2$は変わらないものと考えてください。

垂線がグラム・シュミットの直交化法で得られるベクトルと同一であることの確認

下の図のように、$\boldsymbol{v}_2$から基底$\boldsymbol{u}_1$へおろした垂線との交点をさすベクトルを$\alpha \boldsymbol{u}_1$とします。

$\boldsymbol{v}_2-\alpha\boldsymbol{u}_1$を$\boldsymbol{u}_2$とすると、$\boldsymbol{u}_2$は$\boldsymbol{u}_1$へ下した垂線であるので、

\begin{align}
\langle \boldsymbol{u}_1, \boldsymbol{u}_2\rangle
&=\langle \boldsymbol{u}_1,\boldsymbol{v}_2-\alpha \boldsymbol{u}_1\rangle\\
&=\langle \boldsymbol{u}_1,\boldsymbol{v}_2\rangle-\alpha\langle \boldsymbol{u}_1,\boldsymbol{u}_1\rangle\\
&=\langle \boldsymbol{u}_1,\boldsymbol{v}_2\rangle-\alpha \langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle\\
&=0\\ \\
\alpha&=\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_2\rangle}{ \langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}
\end{align}

より、

\begin{align}
\boldsymbol{u}_2&=\boldsymbol{v}_2-\alpha \boldsymbol{u}_1\\
&=\boldsymbol{v}_2-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_2\rangle}{ \langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1
\end{align}

と表すことができます。

直観的な理解（ベクトルが$3$個の場合）

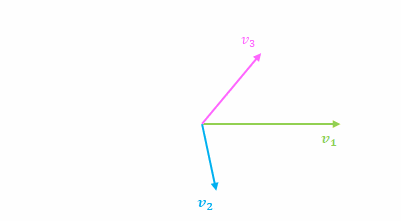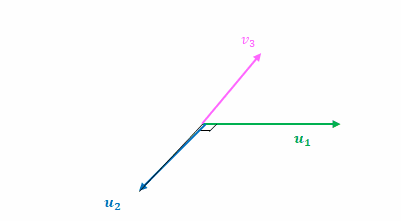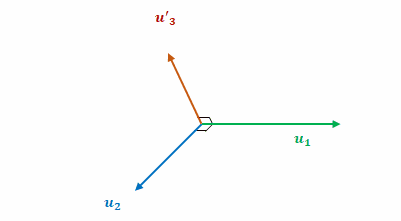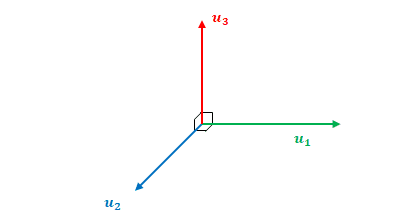
前節と同様に、ユークリッド空間に線形独立なベクトル$\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\}$があり、順にあるベクトルから別のベクトルに垂線を下ろすことにより$3$つの直交するベクトルが得られるところを考えてみましょう。

グラム・シュミットの直交化法は以下の通りです。

\begin{align}
\boldsymbol{u}_1&=\boldsymbol{v}_1 \tag{4}\\
\boldsymbol{u}_2&=\boldsymbol{v}_2-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_2 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1 \tag{5}\\
\boldsymbol{u}_3&=\boldsymbol{v}_3-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_3 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1
-\frac{\langle \boldsymbol{u}_{2},\boldsymbol{v}_3 \rangle}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2} \tag{6}
\end{align}

ただしここでは、

\begin{align}
\boldsymbol{u}’_3=\boldsymbol{v}_3-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_3 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1 \tag{7}
\end{align}

と定義し、上の$3$行目にこれを代入して、

\begin{align}
\boldsymbol{u}_3&=\boldsymbol{u}’_3
-\frac{\langle \boldsymbol{u}_{2},\boldsymbol{v}_{3} \rangle}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2}\\
&=\boldsymbol{u}’_3
-\frac{\langle \boldsymbol{u}_{2},\boldsymbol{u}’_{3} \rangle}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2}\\
\tag{8}
\end{align}

とします。

(8)の等式が成り立つことの確認

$(7)$を移項し、
\begin{align}
\boldsymbol{v}_3=\boldsymbol{u}’_3+\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_3 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1
\end{align}

これを$(8)$の$1$行目に代入し、
\begin{align}
\boldsymbol{u}_3&=\boldsymbol{u}’_3
-\langle \boldsymbol{u}_{2},\boldsymbol{v}_{3} \rangle\frac{1}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2}\\
&=\boldsymbol{u}’_3
-\langle \boldsymbol{u}_{2},\boldsymbol{u}’_3+\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_3 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1 \rangle\frac{1}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2}\\
&=\boldsymbol{u}’_3
-\frac{\langle \boldsymbol{u}_{2},\boldsymbol{u}’_{3} \rangle}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2}-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_3 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle} \frac{\langle \boldsymbol{u}_2,\boldsymbol{u}_1\rangle}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2}\\
\end{align}

$\boldsymbol{u}_1$と$\boldsymbol{u}_2$は直交するので、
\begin{align}
\boldsymbol{u}_3
&=\boldsymbol{u}’_3
-\frac{\langle \boldsymbol{u}_{2},\boldsymbol{u}’_{3} \rangle}{\langle \boldsymbol{u}_{2},\boldsymbol{u}_{2} \rangle}\boldsymbol{u}_{2}\\
\end{align}

これで$\boldsymbol{u}’_3$は$\boldsymbol{v}_3$から$\boldsymbol{u}_1$へ下した垂線、$\boldsymbol{u}_3$は$\boldsymbol{u}’_3$から$\boldsymbol{u}_2$へ下した垂線と考えることができます。

$(4)\ \boldsymbol{u}_1$

$\boldsymbol{u}_1=\boldsymbol{v}_1$とします。

$(5)\ \boldsymbol{u}_2$

$\boldsymbol{v}_2$より$\boldsymbol{u}_1$へ垂線を下ろし、これを$\boldsymbol{u}_2$とします。

$(7)\ \boldsymbol{u}’_3$

$\boldsymbol{v}_3$より$\boldsymbol{u}_1$へ垂線を下ろし、これを$\boldsymbol{u}’_3$とします。

$(8)\ \boldsymbol{u}_3$

$\boldsymbol{u}’_3$より$\boldsymbol{u}_2$へ垂線を下ろし、これを$\boldsymbol{u}_3$とします。

u₃がu₁と直交することの確認

$\boldsymbol{u}_3$は$\boldsymbol{u}’_3$より$\boldsymbol{u}_2$へ下した垂線としたので、スカラー$\beta$を用いて

$$\boldsymbol{u}_3 = \boldsymbol{u}’_3- \beta \boldsymbol{u}_2$$

と表すことができます。$\boldsymbol{u}’_3$と$\boldsymbol{u}_1$、$\boldsymbol{u}_2$と$\boldsymbol{u}_1$が直交するので、

\begin{align}
\langle \boldsymbol{u}_3,\boldsymbol{u}_1\rangle&= \langle \boldsymbol{u}’_3,\boldsymbol{u}_1\rangle- \beta \langle \boldsymbol{u}_2,\boldsymbol{u}_1\rangle\\
&=0
\end{align}

したがって$\boldsymbol{u}_3$は$\boldsymbol{u}_1$と直交します。

これらをまとめたものが以下です。

定理

以下、$V$が内積空間、${\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_n}$が$V$の線形独立な要素で、次の関係にあるとします。

\begin{align}
\boldsymbol{u}_1&=\boldsymbol{v}_1\\
\boldsymbol{u}_2&=\boldsymbol{v}_2-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_2 \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1\\
&\vdots\\
\boldsymbol{u}_n&=\boldsymbol{v}_n-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_n \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1-\cdots – \frac{\langle \boldsymbol{u}_{n-1},\boldsymbol{v}_{n} \rangle}{\langle \boldsymbol{u}_{n-1},\boldsymbol{u}_{n-1} \rangle}\boldsymbol{u}_{n-1}
\end{align}

定理1

$\{\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_n\}$は直交集合である。

証明

数学的帰納法によって示す。

$n=1$の場合、

$$\boldsymbol{u}_1=\boldsymbol{v}_1$$

$2 \le n$とし、$\{\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{n-1}\}$が直交集合あるいは要素が$1$つだけであるときに$\boldsymbol{u}_n$がこれらの要素すべてと直交することを示す。

$2 \le k \le n-1$とすると、

\begin{align}
\langle \boldsymbol{u}_n,\boldsymbol{u}_k\rangle
&=\langle \boldsymbol{v}_n ,\boldsymbol{u}_k\rangle\\
&-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_n \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\langle \boldsymbol{u}_1, \boldsymbol{u}_k \rangle
-\cdots
-\frac{\langle \boldsymbol{u}_{n-1},\boldsymbol{v}_n \rangle}{\langle \boldsymbol{u}_{n-1},\boldsymbol{u}_{n-1} \rangle}\langle \boldsymbol{u}_{n-1}, \boldsymbol{u}_k \rangle
\end{align}

右辺の第$2$項以降の各項を$1 \le i \le n-1$により

$$\frac{\langle \boldsymbol{u}_i,\boldsymbol{v}_n \rangle}{\langle \boldsymbol{u}_i,\boldsymbol{u}_i \rangle}\langle \boldsymbol{u}_i, \boldsymbol{u}_k \rangle$$

と表すと、$i \ne k$のときは$u_i$と$u_k$は直交し$0$となり、$i=k$の項だけが残るので、

\begin{align}
\langle \boldsymbol{u}_n,\boldsymbol{u}_k\rangle
&=\langle \boldsymbol{v}_n ,\boldsymbol{u}_k\rangle
-\frac{\langle \boldsymbol{u}_k,\boldsymbol{v}_n \rangle}{\langle \boldsymbol{u}_k,\boldsymbol{u}_k \rangle}\langle \boldsymbol{u}_k, \boldsymbol{u}_k \rangle\\
&=\langle \boldsymbol{v}_n ,\boldsymbol{u}_k\rangle
-\langle \boldsymbol{u}_k ,\boldsymbol{v}_n\rangle\\
&=0
\end{align}

以上、

$n=1$のとき、$\boldsymbol{u}_1=\boldsymbol{v}_1$

$2 \le n$のとき、$\{\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{n-1}\}$が直交集合または要素が$1$つだけである場合、$\boldsymbol{u}_n$はこれらの要素と直交する。

したがって$\{\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{n}\}$は直交集合である。

■

定理2

$$\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_n)=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_n)$$

証明

数学的帰納法によって示す。

$n=1$では明らかに$\mathrm{span}(\boldsymbol{v}_1)=\mathrm{span}(\boldsymbol{u}_1)$となる。

$2 \le k \le n$のとき、

$$\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{k-1})=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{k-1})$$

の関係にあるとして、

$$\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{k})=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{k})$$

が成り立つことを示す。

グラム・シュミットの直交化法の式の一つ、

$$\boldsymbol{u}_k=\boldsymbol{v}_k-\frac{\langle \boldsymbol{u}_1,\boldsymbol{v}_k \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1-\cdots – \frac{\langle \boldsymbol{u}_{k-1},\boldsymbol{v}_{k} \rangle}{\langle \boldsymbol{u}_{k-1},\boldsymbol{u}_{k-1} \rangle}\boldsymbol{u}_{k-1}$$

を移項し、

$$\boldsymbol{v}_k=\boldsymbol{u}_k+\frac{\langle \boldsymbol{k}_1,\boldsymbol{v}_k \rangle}{\langle \boldsymbol{u}_1,\boldsymbol{u}_1 \rangle}\boldsymbol{u}_1-\cdots – \frac{\langle \boldsymbol{u}_{k-1},\boldsymbol{v}_{k} \rangle}{\langle \boldsymbol{u}_{k-1},\boldsymbol{u}_{k-1} \rangle}\boldsymbol{u}_{k-1}$$

これは$\boldsymbol{v}_k$が$\{\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_k\}$の線形結合であるということなので、

$$\boldsymbol{v}_k \in \mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_k)\tag{1}$$

仮定にて、

$$\mathbb{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{k-1})=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{k-1})$$

としたので、

$$\mathbb{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{k-1}) \subseteq \mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{k})\tag{2}$$

$(1)$と$(2)$より、

\begin{align}
\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_k)\subseteq \mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_k)
\end{align}

$\{\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots\boldsymbol{v}_k\}$と$\{\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots\boldsymbol{u}_k\}$はどちらも線形独立であるので、

$$\mathrm{dim}(\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots\boldsymbol{v}_k))=\mathrm{dim}(\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots\boldsymbol{u}_k))$$

したがって、

$$\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_k)=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_k)$$

以上、

$n=1$のとき、

$$\mathrm{span}(\boldsymbol{v}_1)=\mathrm{span}(\boldsymbol{u}_1)$$

$2 \le k \le n$のとき、

$$\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{k-1})=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{k-1})\\
\Rightarrow \mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{k})
=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{k}) $$

であるのですべての場合において$\mathrm{span}(\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_{n})
=\mathrm{span}(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_{n})$が成り立つ。

■

線形代数 – グラム・シュミットの直交化法

定義

直観的な理解（ベクトルが\(2\)個の場合）

直観的な理解（ベクトルが\(3\)個の場合）

定理