「マクスウェルの方程式1-4」で4つの式についてそれぞれ述べました。本ページは、マクスウェルの方程式とは直接関係ありませんが、電磁波との関係について説明します。マクスウェルが式を発表した当時、電磁波の存在は知られていませんでしたが、マクスウェルは自らの式より理論的に電磁波の存在を予言しました。どうやって導き出せるのか、我々も考えてみましょう。
電磁波の理解には波動方程式が必要だと思います。本ページの分量はそれほど多くありませんが、波動方程式については別ページで述べていますのでご注意ください。
1 直観的な理解1
1.1 マクスウェル – ファラデーの式とアンペール – マクスウェルの式からの理解
改めて、微分形のマクスウェルの方程式です。
電荷はないものとし、ガウスの法則の右辺は\(0\)とします。
導体を流れる電流もないものとし、アンペール – マクスウェルの式の(元の)第1項も\(0\)とします。
$$\nabla \cdot \boldsymbol{E} = 0 $$
$$ \nabla \cdot \boldsymbol{B} = 0 $$
$$ \nabla \times \boldsymbol{E} = – \frac {\partial \boldsymbol {B}} {\partial t} $$
$$ \nabla \times \boldsymbol{B} = \epsilon_0 \mu_0 \frac {\partial \boldsymbol {E} } { \partial t} $$
マクスウェル – ファラデーの式とアンペール – マクスウェルの式をみると、なんとなく電場と磁場が相互に作用し空間を伝播していくように思えます。以下のような感じです。
ある位置において変位電流があり、時間経過とともに下から上の方向へ大きくなったとします。
アンペール – マクスウェルの式が示す通り、変位電流の変化により磁場が発生します。
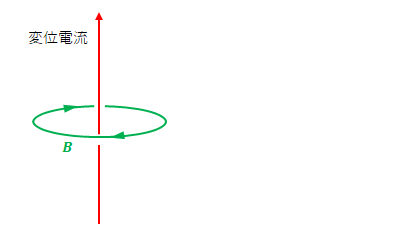
マクスウェル – ファラデーの式の通り、磁場の変化により電場が発生します。
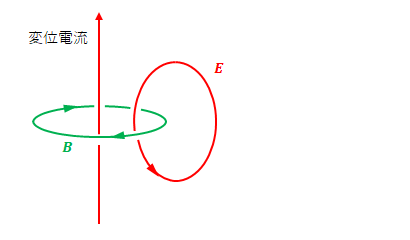
同じように磁場・電場の発生を繰り返し伝播していきます。
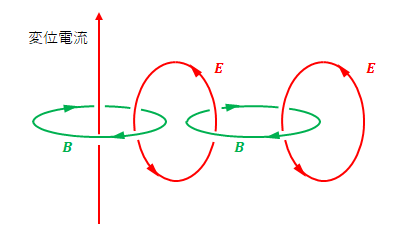
このイメージは、電場と磁場の変化が互いに影響を与え、それが波になるという点で間違いではありません。
しかしもっと複雑に様々な方向へ伝播するのではないでしょうか。
実はこのイメージには考えなくてもよい成分が含まれています。また、もっと条件を追加し簡略化して考えることができます。
次章では条件を簡略化しながら1次元波動の導出をします。1次元波動方程式が成立することがわかれば、マクスウェルの方程式が電磁波の伝播を示していることが確認できるはずです。
また、3章では簡略化した式から改めて直観的な理解をしてみます。
2 1次元波動方程式の導出
2.1 座標と電場・磁場の各成分の定義
次の図のような座標を考えます。
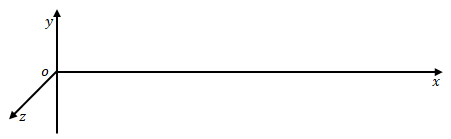
原点にて\(y\)軸方向に変位電流があり時間とともに変化するとします。

電場の\(x\)、\(y\)、\(z\)方向の成分をそれぞれ\(E_x\)、\(E_y\)、\(E_z\)、地場を\(B_x\)、\(B_y\)、\(B_z\)とします。
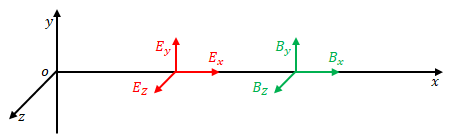
マクスウェルの方程式は電場・磁場の空間または時間に関する偏微分の関係を表したものです。
偏微分の組み合わせはこれだけあります。

例えば\(\partial {E_z} \partial {z}\)は、\(z\)方向に進むにつれて\(z\)方向の電場の成分が変化する場合に値が現れます。\(\partial {E_z} \partial {y}\)は\(y\)方向に進むにつれて\(z\)方向の電場の成分が変化する場合に値が現れます。
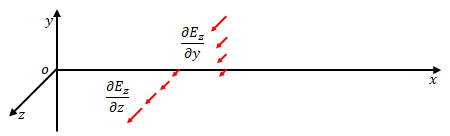
次節より、これらのうち考慮が不要な項目を除外し、不要でない項目は関係式を導きます。除外した項は常に\(0\)となります。
2.2 \(y\)方向と\(z\)方向の空間依存の除外
まず、前提条件として、電場・磁場は\(y\)方向・\(z\)方向の変化はないということにします(時間経過による変化は別です)。つまり\(y\)、\(z\)について偏微分する成分は除外します。

これは電場・磁場の進行方向を\(x\)方向のみに決めている、つまり電磁波が1次元であるとしているということになります。本来電磁波は3次元として考えるべきですが、ここでは単純化して考察を進めます。
2.3 ガウスの法則の適用
ここまでマクスウェル – ファラデーの式とアンペール – マクスウェルの式に注目してきましたが、ガウスの法則と磁場に関するガウスの法則も関係があります。両者を空間成分で分けて記述すると以下です。
$$\frac {\partial E_x}{\partial x} + \frac {\partial E_y}{\partial y} + \frac {\partial E_z}{\partial z} = 0 $$
$$\frac {\partial B_x}{\partial x} + \frac {\partial B_y}{\partial y} + \frac {\partial B_z}{\partial z} = 0 $$
すでに\(\displaystyle \frac {\partial E_y}{\partial y} = 0\)、\(\displaystyle \frac {\partial E_z}{\partial z} = 0\)であることがわかっています。したがって、
$$\displaystyle \frac {\partial E_x}{\partial x} = 0$$
同様に、
$$\displaystyle \frac {\partial B_x}{\partial x} = 0$$
です。
既に、電磁波が伝播するとすればそれは\(x\)方向であると限定しています。後述の1次元波動方程式により、そのことが確かめられます。
さらに上の2式は進行方向の電場・磁場の変動成分がないということを示しています。つまり電磁波は横波であるということごわかります。

2.4 マクスウェル – ファラデーの式とアンペール – マクスウェルの式の適用
以下が成分ごとに表したマクスウェル – ファラデーの式とアンペール – マクスウェルの式です。
$$
\left ( \frac {\partial {E_z}} {\partial {y}} – \frac {\partial {E_y}} {\partial {z}} \right) \boldsymbol {i} + \left ( \frac {\partial {E_x}} {\partial {z}} – \frac {\partial {E_z}} {\partial {x}} \right) \boldsymbol {j} + \left ( \frac {\partial {E_y}} {\partial {x}} – \frac {\partial {E_x}} {\partial {y}} \right ) \boldsymbol {k} \\
= -\frac {\partial {B_x}} {\partial {t}}\boldsymbol {i} – \frac {\partial {B_y}} {\partial {t}} \boldsymbol {j} – \frac {\partial {B_z}} {\partial {t}} \boldsymbol {k}
$$
$$
\left ( \frac {\partial {B_z}} {\partial {y}} – \frac {\partial {B_y}} {\partial {z}} \right) \boldsymbol {i} + \left ( \frac {\partial {B_x}} {\partial {z}} – \frac {\partial {B_z}} {\partial {x}} \right) \boldsymbol {j} + \left ( \frac {\partial {B_y}} {\partial {x}} – \frac {\partial {B_x}} {\partial {y}} \right ) \boldsymbol {k} \\
= \epsilon_0 \mu_0 \left (\frac {\partial {E_x}} {\partial {t}}\boldsymbol {i} + \frac {\partial {E_y}} {\partial {t}} \boldsymbol {j}+ \frac {\partial {E_z}} {\partial {t}} \boldsymbol {k} \right )
$$
これらの式に前節まで\(0\)としてきた偏微分の項を適用します。
まず、マクスウェル – ファラデーの式についてです。左辺と右辺の\(\boldsymbol i\)、\(\boldsymbol j\)、\(\boldsymbol k\)の係数の関係に注目してください。
\(\boldsymbol i\)の項から順に、
\(\displaystyle \frac {\partial {E_z}} {\partial {y}} = \frac {\partial {E_y}} {\partial {z}} = 0\)より
$$\frac {\partial {B_x}} {\partial {t}} = 0$$
\(\displaystyle \frac {\partial {E_x}} {\partial {z}} = 0\)より
$$\frac {\partial {E_z}} {\partial {x}} = \frac {\partial {B_y}} {\partial {t}}$$
\(\displaystyle \frac {\partial {E_x}} {\partial {y}} = 0\)より
$$\frac {\partial {E_y}} {\partial {x}} = -\frac {\partial {B_z}} {\partial {t}}$$
アンペール – ファラデーの式からも同様に導かれます。
\(\displaystyle \frac {\partial {B_z}} {\partial {y}} = \frac {\partial {B_y}} {\partial {z}} = 0\)より
$$\frac {\partial {E_x}} {\partial {t}} = 0$$
\(\displaystyle \frac {\partial {B_x}} {\partial {z}} = 0\)より
$$\frac {\partial {B_z}} {\partial {x}} = -\epsilon_0 \mu_0 \frac {\partial {E_y}} {\partial {t}}$$
\(\displaystyle \frac {\partial {B_x}} {\partial {y}} = 0\)より
$$\frac {\partial {B_y}} {\partial {x}} = \epsilon_0 \mu_0 \frac {\partial {E_z}} {\partial {t}}$$

2.5 波源の向きによる制限の追加
前節までで4式が残されました。
次に波源による電場と磁場の向きの制限を追加します。
座標の原点にて\(y\)方向に変位電流が流れ時間とともに変化するものとします。一方で\(z\)方向の電場は時間によって変化しないこととします。
つまり、原点における\(\displaystyle \frac {\partial E_z}{\partial t}\)は常に\(0\)です。原点における\(\displaystyle \frac {\partial E_y}{\partial t}\)は変動するので常に\(0\)というわけではありません。
磁場は電場とは垂直な方向に成分が生じます。ただし\(x\)方向はすでに除外しています。原点における\(\displaystyle \frac {\partial B_z}{\partial t}\)は\(0\)とは限りませんが、原点における\(\displaystyle \frac {\partial B_y}{\partial t}\)は\(0\)です。
以上より2式に絞られます。
$$\frac {\partial {E_y}} {\partial {x}} = -\frac {\partial {B_z}} {\partial {t}}$$
$$\frac {\partial {B_z}} {\partial {x}} = -\epsilon_0 \mu_0 \frac {\partial {E_y}} {\partial {t}}$$

2.6 1次元波動方程式の導出
かなり簡単になりましたが、\(E_y\)と\(B_z\)という2つの関数と\(x\)と\(t\)という2つの変数があり、同時に動くところを頭の中で追うのは難しいかもしれません。
そこで2式より2つの関数2変数の式に変形します。
上の式を\(x\)について偏微分、下の式を\(t\)について偏微分すると、
$$\frac {\partial^2 {E_y}} {\partial^2 {x}} = -\frac {\partial {B_z}} {\partial {x} \partial {t}}$$
$$\frac {\partial^2 {B_z}} {\partial {x} \partial {t}} = -\epsilon_0 \mu_0 \frac {\partial^2 {E_z}} {\partial^2 {t}}$$
\(\displaystyle \frac {\partial^2 {B_z}} {\partial {x} \partial {t}}\)を消去し、
$$\frac {\partial^2 {E_y}} {\partial^2 {t}} = \frac {1}{\epsilon_0 \mu_0} \frac {\partial^2 {E_y}} {\partial^2 {x}}$$
同様に上の式を\(t\)について偏微分、下の式を\(x\)について偏微分し1つの式にまとめると、
$$\frac {\partial^2 {B_z}} {\partial^2 {t}} = \frac {1}{\epsilon_0 \mu_0} \frac {\partial^2 {B_z}} {\partial^2 {x}}$$
この2式はそれぞれ1次元波動方程式とよばれる、偏微分方程式です。
電磁波の波動としての基本的な性質を理解するためには1次元波動方程式の理解が必要です。「1次元波動方程式」で説明をしていますのでぜひご覧ください。
2.7 波源の追加
波動方程式は波の伝播の様子を示しますが、どのような波が発生しているかはこの式からはわかりません。境界条件または初期条件として与える必要があります。
電磁波の場合、波源を境界条件または初期条件として与えなければなりません。ここでは以下を条件とします。
・原点に波源があり、時間経過とともに原点の\(E_y\)が変化する。その関数を\(E_{y2}(t)\)とする。
・\(t=0\)では\(E_y\)は\(0\)。
式にすると以下です。
$$E_y(0,t)=E_{y2}(t)$$
$$E_y(x,0)=0$$
波動方程式と波源の条件の解、つまりこれらを満たす\(E_y(x,t)\)を求めます。
直接の解ではないのですが、「ダランベールの式」(前述のページにあります)を応用して求めることができます。
ダランベールの式の初期条件は以下です。
$$E_y(x,0)=E_{y0}(x) $$
$$\left . \frac {\partial E_y(x,t)} {\partial t} \right |_{t=0} = E_{y1}(x) $$
\(E_{y0}(x)\)と\(E_{y1}(x)\)は初期条件として与えている関数です。
解は以下です。
$$E_y(x,t)=\frac {1}{2} \left ( E_{y0}(x-ct) + E_{y0}(x+ct) \right ) + \frac {1}{2c} \int_{x-ct} ^{x+ct} E_{y1}(s) ds$$
本ページの波源の条件では原点のみで\(E_y(x,t)\)が変化するので積分の項は無限小と考えることができます。解は以下に簡略化できます。
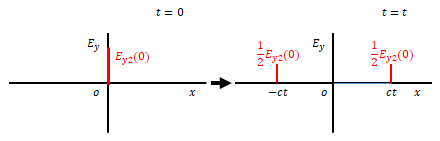
$$E_y(x,t)=\frac {1}{2} \left ( E_{y0}(x-ct) + E_{y0}(x+ct) \right ) $$
これは\(t=0\)のときの\(E_y(x,t)\)つまり\(E_{y0}(x)\)が\(t>0\)において半分に分かれ左右に移動していくことを示しています。
しかし波源は\(t=0\)だけではなく\(t>0\)、\(t<0\)のときの値も\(E_{y2}(t)\)によって定義されています。これが解に反映されなければなりません。
そこで、ダランベールの式の\(t\)を少しずつずらし解を重ね合わせることを考えます。
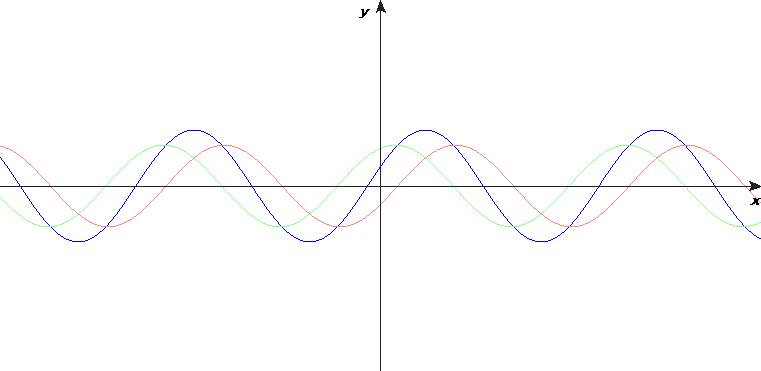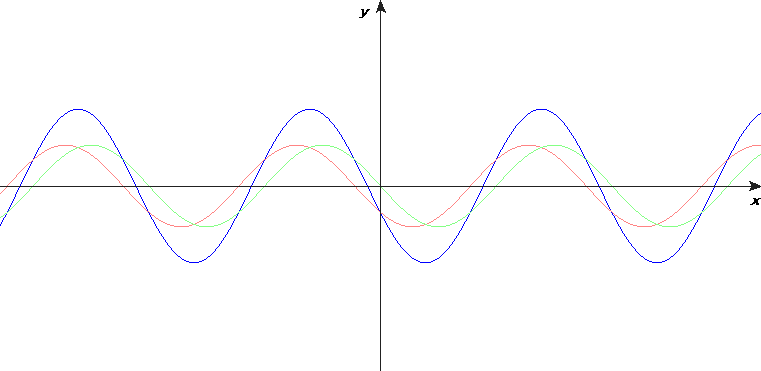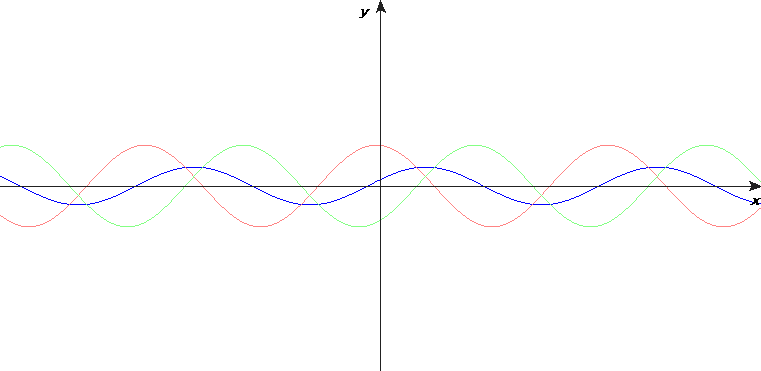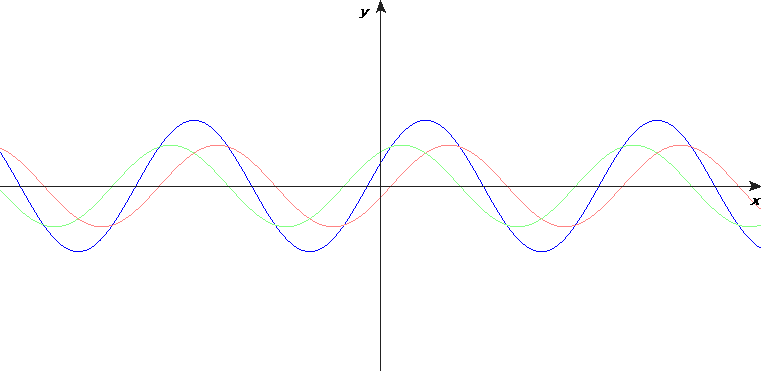
ダランベールの式は、時間\(t\)経過後には\(E_{y2}\)それぞれ半分の大きさになって\(x=\pm ct\)の位置に移動するものだと考えます。図の左側は\(t=0\)、右側は\(t=t\)です。
\(t=t_1\)における原点の\(E_y=E_{y2}(t_1)\)は\(t – t_1\)経過後、つまり\(t=t\)では\(\pm c(t-t_1)\)に移動します。
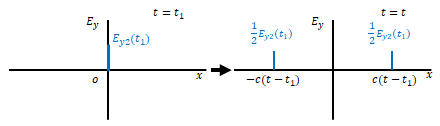
\(t=t_2\)についても同様です。
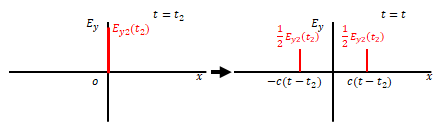
上記は\(t=t_1\)、\(t=t_2\)どちらかに原点で\(E_y\)にパルスが発生していた場合ですが、\(t=t_1\)、\(t=t_2\)どちらでもパルスが発生していた場合は重ね合わせの原理により\(t=t\)では図のようになります。
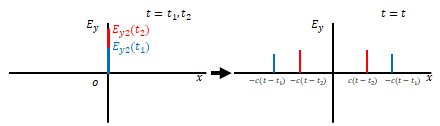
さらに、\(E_y\)が連続的に発生していた場合は\(x\)軸上でも連続的な波形となります。
下の図は原点において\(E_y\)が三角関数であった場合です。
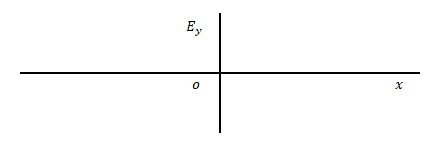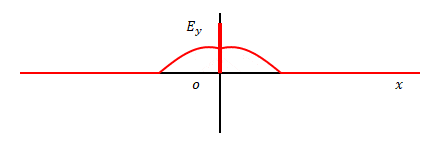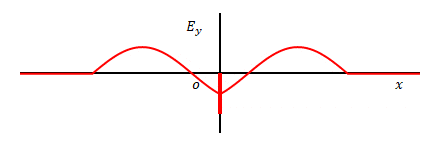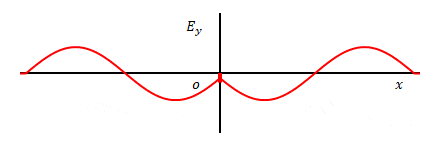
これを式にすると以下です。
$$E_y(x,t)=\frac{1}{2} \left ( E_{y2}(x-ct)+E_{y2}(x+ct) \right ) $$
積分の項を削除した場ダランベールの式と同じです。ダランベールの式では初期条件として\(t=0\)の時の\(E_y(x,t)\)のみを条件としていましたが、本節では\(t=0\)以外の条件も追加しています。これらの条件も上の式に反映されているのですが、\(t=0\)の条件の場合と同じ式で表されるため、式に変化はありません。
以上、本節の波源の条件では、波源の半分の大きさの波が左右に移動することがわかりました。
3 補足:直観的な理解2
2.6節で1次元波動方程式を導きました。
後はこの式の意味を理解することが近道でしょう。
ただ、1次元波動方程式はマクスウェルの方程式よりかなり形を変えていて面白くありません。
そこで、やや蛇足になるかもしれませんが2.5節の以下の式の物理的意味を考えてみます。
$$\frac {\partial^2 {E_y}} {\partial^2 {x}} = -\frac {\partial {B_z}} {\partial {x} \partial {t}}$$
$$\frac {\partial^2 {B_z}} {\partial {x} \partial {t}} = -\epsilon_0 \mu_0 \frac {\partial^2 {E_z}} {\partial^2 {t}}$$
これらの式であれば、マクスウェル – ファラデーの式とアンペール – マクスウェルの式から不要な成分を除外したただけなので(負号の有無はすぐにはわかりませんが)直観で理解する意義はあるかと思います。
結局のところ、これらの式からの電磁波をイメージするのは簡単ではないかもしれません。あと少し変形すると1次元波動方程式が得られます。1次元波動方程式であれば電場、磁場いずれかのみで記述され、もう少し理解しやすいと思います。1次元波動方程式からの直観的な理解については「1次元波動方程式」のページをご覧ください。
さて、本章では横軸が\(x\)の図と\(t\)の図があるので注意してください。また、1章の図はベクトルがつながった状態をイメージして描いていましたが、本章はグラフとして表しています。
2.7節のように原点の\(y\)軸方向に変位電流(これを波源とします)が存在し、時間経過により減少する(負の方向に大きくなる)とします。グラフは以下です。
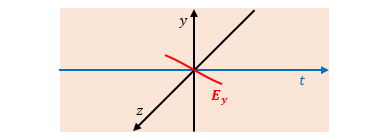
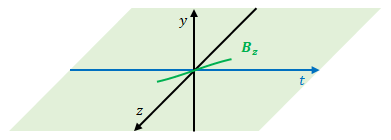
アンペール – マクスウェルの式より、\(B_z\)と\(x\)の関係は以下です。\(x\)が正の象限のみ考慮します。
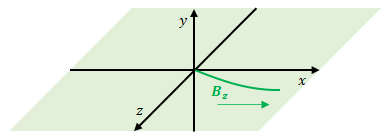
原点における\(B_z\)は時間経過によりどう変化するでしょう。
波源より\(B_z\)が離れていくということは上の図では右の方向に進みます。したがって原点での\(B_z\)は時間経過により減少します。\(z\)軸は手前側が正である点に注意ください。
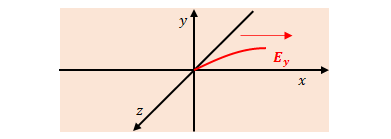
マクスウェル – ファラデーの式より、\(x\)の増加方向に対し\(E_z\)は増加します。\(E_z\)が右方向へ進むと原点では\(E_z\)が時間経過により減少し1番目の図と一致します。
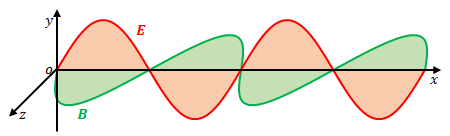
詳細は省略しますが、波源が三角関数であれば電磁波は以下のように空間上で正弦波を描きます。
4 その他
4.1 波源の具体例
本ページではアンペール – マクスウェルの式の第1項を\(0\)とし、第2項の変位電流によって電磁波が生じるとしました。
$$ \nabla \times \boldsymbol{B} = \mu_0 \left( \boldsymbol {J} + \epsilon_0 \frac {\partial \boldsymbol {E} } { \partial t} \right) $$
第1項の、導体を流れる電流によっても電磁波は生じます。その例について簡単に述べます。
下の図の四角は電圧源(信号源)です。信号源に接続される線に互いに反対の位相の電圧を出力します。
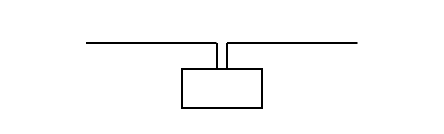
折れ曲がった2本の線は導線で、金属の棒や線です。線の先は何も接続されていません。
導線には電圧が印加されますが、その先に抵抗がないので電流は流れないように思えます。
しかし、伝送路長(導線の長さ)に比べ波長が十分に短い場合(つまり信号が高周波である場合または伝送路が長い場合)、回路は分布定数回路になります。
分布定数回路では電圧・電流は波の性質をもちます。
瞬間的に電圧・電流が回路全体に伝わるわけではなく、時間経過とともに変化し、伝送路の位置によっても値は異なります。先端の電気的状態にかかわらず電流が波となって流れることがあります。この電流によって電磁波が発生します。
我々が普段目にしている回路は集中定数回路です。直流の場合や周波数が低い、伝送路が短い回路は集中定数回路です。前述のように伝送路の先端が解放状態かつ集中定数回路の場合、電圧が印加されていても電流は流れません。
また、分布定数回路では伝送路の性質が異なるところで反射が起きます。この例の場合は線の先端で抵抗値が無限大となるために反射が起き、電圧・電流は信号源に戻り、定在波(定常波)が発生します。定在波とは入射波と反射波の合成による波で、同じ位置にとどまって振幅だけが変化するような波です。定在波が発生すると電磁波の放射は安定します。
位相が反対の信号線が平行して配置されていると両者からの電磁波は打ち消しあいますが、本節の最初の図のよう根本から分岐していると両者は打ち消しあわずに放射します。
このような回路で構成された機器をダイポール・アンテナとよびます。
※常に同じような定在波が発生するわけではなく、伝送路長や反射の度合いによって発生の程度が変わります。
4.2 光速と\(\epsilon_0\)、\(\mu_0\)の関係
電磁波を1次元波動方程式で表した場合の\(\displaystyle \frac{1}{\sqrt{\epsilon_0 \mu_0}}\)は波の速度を表しています。また、実験により電磁波は光の速度と一致することがわかっています。したがって\(c\)を光速とすると、
$$c= \frac {1}{\sqrt{\epsilon_0 \mu_0}}$$
という関係にあります。
「マクスウェルの方程式 1(ガウスの法則)」で述べましたが、本サイトではMKSA単位系でマクスウェルの方程式を表しています。MKSA単位系の場合はマクスウェルの方程式に\(\epsilon_0\)と\(\mu_0\)が現れます。
MKSA単位系では\(\mu_0\)は\(4\pi \times 10^{-7} N A^{-2}\)と定義されています。\(\epsilon_0\)は\(c\)と\(\mu_0\)より決まり、約\(8.85 \times 10^{-12} F m^{-1}\)と定義されています。
※これらは測定により決められており、正確にこの値というわけではありません。
5 まとめ
本ページでは以下の条件と手順によりマクスウェルの方程式より1次元波動方程式を導きました。
・電場と磁場は\(y\)方向と\(z\)方向の空間依存はない(これらの方向には変化しない)という制限追加により
$$\frac {\partial **}{\partial y} = 0$$
$$\frac {\partial **}{\partial z}=0$$
ただし**は電場・磁場の各成分です。
・ガウスの法則、磁場に関するガウスの法則により
$$\frac {\partial E_x}{\partial x}=0$$
$$\frac {\partial B_x}{\partial x}=0$$
・マクスウェル – ファラデーの式より
$$\frac {\partial {B_x}} {\partial {t}} = 0$$
$$\frac {\partial {E_z}} {\partial {x}} = \frac {\partial {B_y}} {\partial {t}}$$
$$\frac {\partial {E_y}} {\partial {x}} = -\frac {\partial {B_z}} {\partial {t}}$$
・アンペール – マクスウェルの式より
$$\frac {\partial {E_x}} {\partial {t}} = 0$$
$$\frac {\partial {B_z}} {\partial {x}} = -\epsilon_0 \mu_0 \frac {\partial {E_y}} {\partial {t}}$$
$$\frac {\partial {B_y}} {\partial {x}} = \epsilon_0 \mu_0 \frac {\partial {E_z}} {\partial {t}}$$
・波源が\(y\)方向にのみ変化するという制限追加により
$$\frac {\partial {E_z}} {\partial {t}} = 0$$
$$\frac {\partial {B_y}} {\partial {t}} = 0$$
・以上より残った式は
$$\frac {\partial {E_y}} {\partial {x}} = -\frac {\partial {B_z}} {\partial {t}}$$
$$\frac {\partial {B_z}} {\partial {x}} = -\epsilon_0 \mu_0 \frac {\partial {E_y}} {\partial {t}}$$
・式を変形し、
$$\frac {\partial^2 {E_y}} {\partial^2 {t}} = \frac {1}{\epsilon_0 \mu_0} \frac {\partial^2 {E_y}} {\partial^2 {x}}$$
$$\frac {\partial^2 {B_z}} {\partial^2 {t}} = \frac {1}{\epsilon_0 \mu_0} \frac {\partial^2 {B_z}} {\partial^2 {x}}$$
これらが波動方程式です。
