月が年に3cm地球から離れていることをご存じでしたか。わかりやすく説明された書籍やWebサイトがありますので概要の理解はそれほど難しくないでしょう。
ただし、物理の法則に則って原理を理解しようとすると意外に簡単ではありません。拙著でもこの現象を取り上げましたが、説明しきれないところは補足として分けて数式を使っています。
わかっていただけるものと信じていますが、かねてからWebで補足ができたらなあ、とも思っていました。
そこで、ここでは月が遠ざかっていく様子をシミュレートします。
(1)潮汐力のどの成分が影響するのか
月が地球から遠ざかる原因は潮汐力、つまり地球から受ける重力です。月が引っ張られる力は完全に地球を向いているわけではありません。地球には潮汐があります。しかし、地球の中心から見ると満潮の位置と月の方角は同一線上にはありません。常に満潮が月の公転の先をいくようになっています
これにより、月が公転の方向へ引っ張られるようになります。
半径の方向を無視すると以下が残ります。これが月の公転の軌道を少しずつ変えていきます。
(2)進行方向を向く力によって月はどのように軌道を変えるか
重力によって月が円運動をしている状態で月の公転の進行方向に力が加わったら軌道はどう変わるでしょう。
外へずれます。月は地球から離れていきます。これはイメージ通りではないでしょうか。月は加速されるわけなので、勢いがついて外へ向こうとするのです。
では月の速度はどうなるでしょう。通常、円運動を行う物体の速さは角速度で表します。直線の場合の速度に半径をかけた値です。
角速度は小さくなるのです。ミニチュアサイズの地球と月があったとします。あなたがその月を進行方向に押したとします。押せば押すほど月は遅くなるのです。
ちなみに、もし月の進行方向とは逆向きに力が加わった場合、公転の半径は小さくなり、角速度は大きくなります。
さらに不思議なことがあります。もし月が軌道の外側、つまり地球とは反対向きに外から力が加わったらどう変化するでしょう。力の分だけ外にずれますが、その力と遠心力の和が重力とつり合うところで安定します。内側向きの力の場合も同様です。
進行方向(およびその逆方向)に力が加えられ続ける限り、半径と角速度は変わり続けますが、外側・内側の場合はそうではないのです。
なぜそうなるかは省略します。
(3)月のエネルギーはどう変わる?
シミュレーションの前にエネルギーについて考えてみます。運動エネルギーの式を覚えているでしょうか。
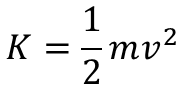
でしたね。これは直線の場合です。円運動の場合は角速度ωと半径rにより以下のように表されます。
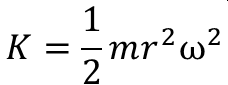
進行方向に力が加えられる場合、運動エネルギーは大きくなるのでしょうか。半径は大きくなるのですが角速度が小さくなるので運動エネルギーは小さくなります。押しているのに運動エネルギーが小さくなるのでしょうか。そのエネルギーはどこへいったのでしょう。
位置エネルギーです。位置エネルギーは基準とする点から高い位置にあるほど大きくなります。月の位置エネルギーも同様です。もし地球から離れる場合、その位置エネルギーは大きくなります。
(4)シミュレーション
ここまで、ちょっと複雑なところがあったかもしれませんが、とにかくシミュレーションを実行してみます。
前提は以下の通りです。
地球と月の間には重力があります。これは以下のように表すことができます。
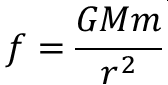
ただし、
G:万有引力定数 6.67 Nm2kg-2
M:地球の質量 5.97 × 1024kg
m:月の質量 7.35 × 1022kg
r:公転の半径 3.85 × 108m
です。
ただしシミュレーションでは都合によりこれらの値を変えています。
下のいずれかのボタンを押すと始まります。ボタンの意味は次の通りです。
順:公転の進行方向に力が加わる
逆:公転の進行とは反対の方向に力が加わる
外:外向きに力が加わる
内:内向きに力が加わる
右のグラフは横軸を時間として各値を表示しています。位置エネルギーは無限遠を0としています。地球に近づくほど小さくなるのでマイナスの値です。違和感があるかもしれませんが地球の中心を基準とすることができないためにこのようにしています。

(5)まとめ
シミュレーションで、以下のことが確認できると思います。
・進行方向に力が加わると半径は大きく、角速度は小さくなり続ける。
・進行方向とは反対向きに力が加わると半径は小さく、角速度は大きくなり続ける。
・外側・内側に向けて力が加わると半径と角速度は一定。ただし(このグラフからは違いを確認できませんが)重力(円運動としてみた場合は向心力)と遠心力がつり合うよう変化している。
月の公転運動は潮汐力により継続的に進行方向に力が加えられています。この力により月は地球から遠ざかっているのです。
