結果の「場合の数」が2で、その確率が一定である試行をベルヌーイ試行とよびます。コイントスがそうですね。
\(n\)回の試行を1組とし、その累積の値(たとえば表が出た回数)を記録するとします。複数組実施した場合、それぞれの累積の値はばらつきます。この値と出現頻度の関係は二項分布で表すことができます。
二項分布の定義を確認し、シミュレーションをします。
(1)二項分布とは?
次のような例を考えてみます。
壺の中に白と黒の玉があります。1個取り出して戻します。白が出る確率は0.6、黒が出る確率は0.4です。3回行います。白が2個、黒が1個の確率はどれだけでしょう。
これは白が2個の「場合の数」とそれぞれの確率をかけることによって求めることができます。
白が2個の場合の数は3です。
組み合わせの記号を使い以下のように表現できます。
\( {}_3 C_2 \)
つまり、3個中から2個を抽出した場合の組み合わせです。
それぞれの確率は、白の0.6が2回、黒の0.4が1回なので、以下となります。
\( {}_3 C_2 \times 0.6^2 \times 0.4^1\)
一般化しましょう。n回玉を取り出して、そのうちk回が白だった場合の確率を式にします。上記の3を\(n\)、2を\(k\)、0.6を\(p\)、0.4を\(1-p\)とします。
\( {}_n C_k p^k(1 – p)^{n-k}\)
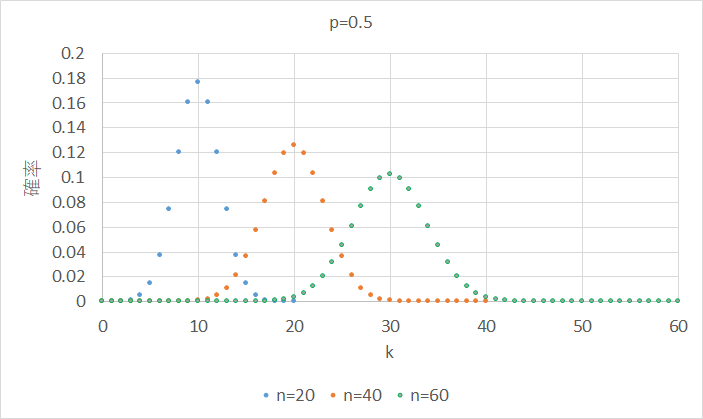
どのような分布になるかみてみましょう。下図は\(n\)の数を大きくし、\(p\)を0.5とした場合です。\(n\)を固定の値とし、横軸を\(k\)、縦軸を確率としています。二項分布は離散分布であり連続した分布ではないため、ここでは点で示しています。\(n\)の半分のところが最も高い確率となっています。
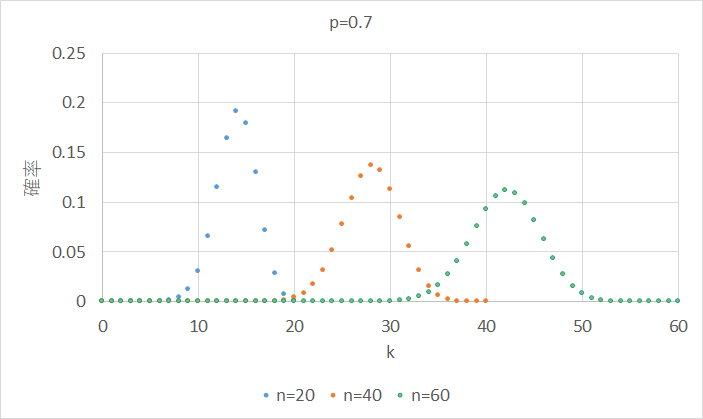
下の図は\(p\)を0.7とした場合です。山の形は\(p\)が0.5のときと大きく変わりませんが、最頻値(モード)は右に寄っています。
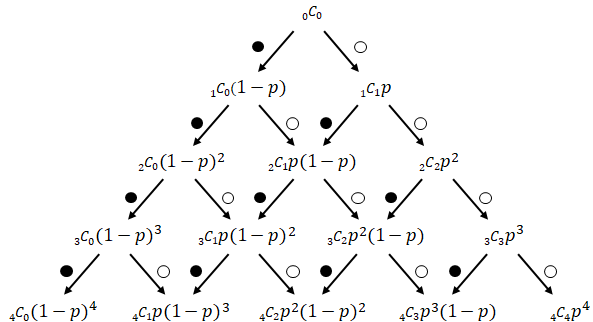
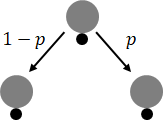
(2)ベルヌーイ試行を図で表すと
図のように一度試行し白だった場合は右下、黒だった場合は左下に矢印が引かれるとします。
さらにもう一度試行すると次のようになります。真ん中は右からと左からの流れが重なり、係数が2となります。
4段目まで展開すると次のようになります。
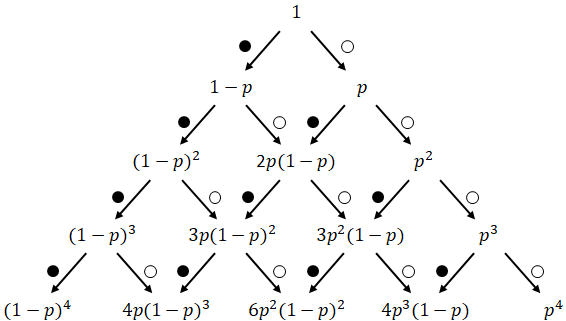
\(n\)回試行し、\(k\)回白が出た場合は図の\(n\)段目(一番上が0)、左から\(k\)番目(一番左が0)になるはずです。1回試行するごとに下の段へ移動し、1回白が出るごとに右へ移動するからです。
係数が一致するか確認してみましょう。冒頭の例の、3回試行し白が2回だった場合、0段目からの経路は3通りあります。
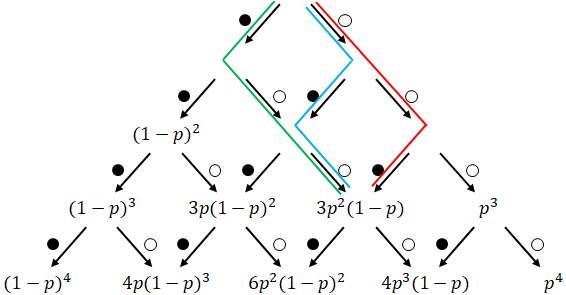
各経路の、試行の結果を1回目から並べると必ず白と黒の並びは異なります。
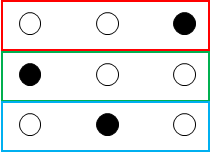
つまり、\(n\)個の中から\(k\)個の組み合わせの数と同じです。上の図の係数を組み合わせの数に置き換えると次のようになります。
(3)二項分布の例1
動画をご覧ください。
積みあがっている球の高さと横の位置の関係をグラフに見立てると何になるでしょう。
球が釘に当たる様子をみてみます。各段で必ず釘に当たり、当たった球は\(p\)の確率で右、\(1-p\)の確率で左へ移動するとします。図はその様子を示しています。小さい丸が釘、大きい丸が球です。
下段を追加していくとどうなるでしょう。前項の三角形と同じですね。つまり、二項分布になるのです。
(4)二項分布の例2
量子力学や株式投資などで使われるランダムウォークという運動も、二項分布として考えることができます。
下の図は一次元のランダムウォークです。この場合は一定時間ごとに物体の位置が同じ確率・距離で左右に移動する様子を示しています。n回移動したときにkの位置にいる確率は二項分布になります。
ちなみに、次の図は二次元にした場合です。移動単位と時間を小さくしていけばブラウン運動に近似することができます。
一次元の場合に戻りましょう。横軸が変位、縦軸が時間とするとどうでしょう。やはり(2)の三角形のようになるはずです。つまり、移動距離は二項分布になります。
(4)シミュレーション
\(n\)を10とした場合のシミュレーションです。前述(3)のような釘に当たって球が流れる様子をイメージしています。左右に移動する確率は初期値で0.5です。変更する場合はテキストボックスに0.1-0.9の値を入力し「p」を押してください。値が大きいほど右へ移動する確率が高くなります。終了後、二項分布の理論値を赤丸で表示します。
