微分を理解したいが難しそうだから避けている、という人は多いのではないでしょうか。本ページではなるべくわかりやすくするために、図を中心にその概念を説明してみました。
1 位置・時間と速度の関係
物体が一定の速度で動き続けているとします。時間を\(x\)、位置を\(y\)、速度を\(v\)で表します。物理学では時間は\(t\)で表すことが多いのですが、ここでは数学でよく使われる\(x\)にします。\(x=0\)の時に\(y=0\)であったとすると、
$$v=\frac{y}{x}$$
の関係にあります。
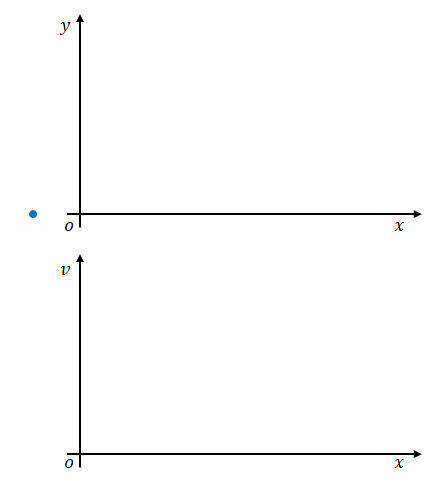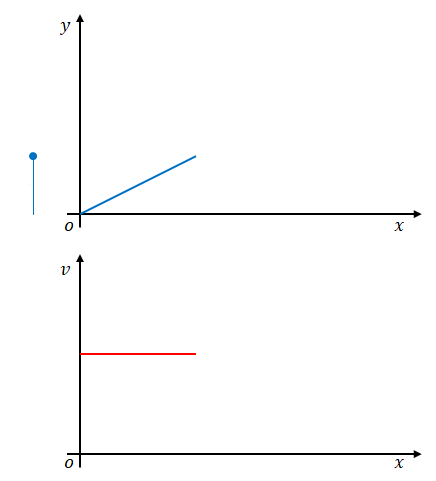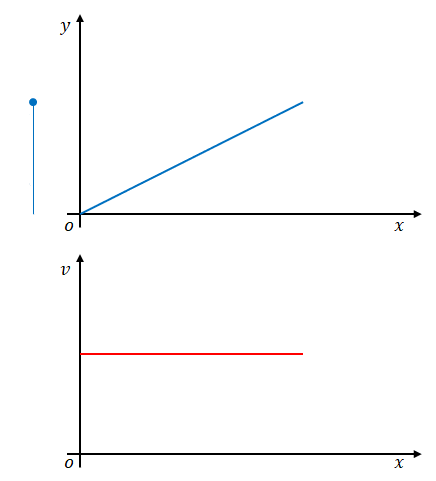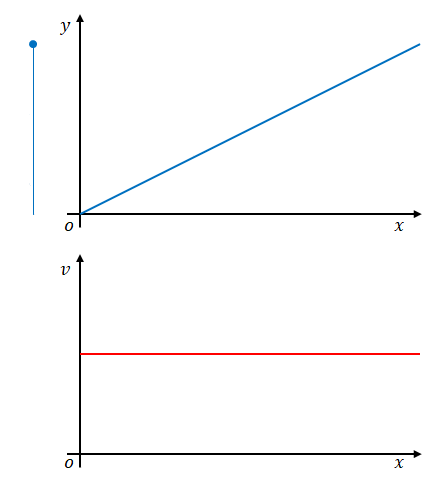
では、下の図のように速度が変化する場合、時間と位置より求めるにはどうしたらよいでしょうか。
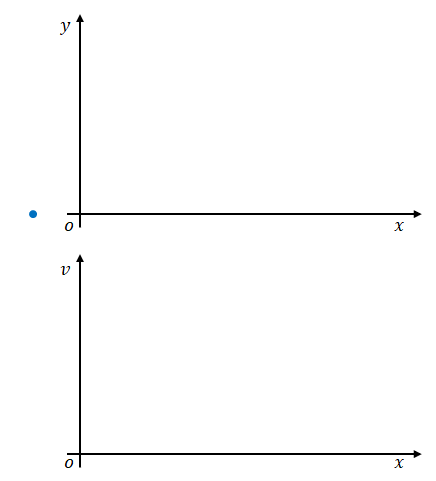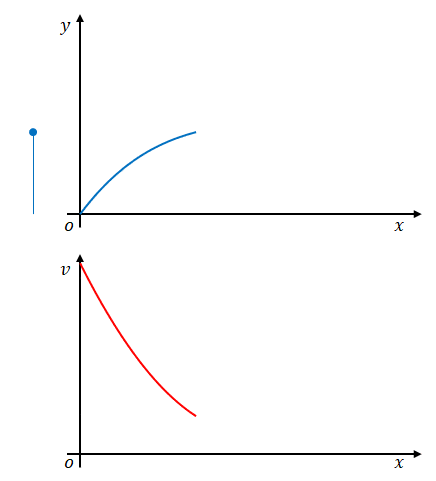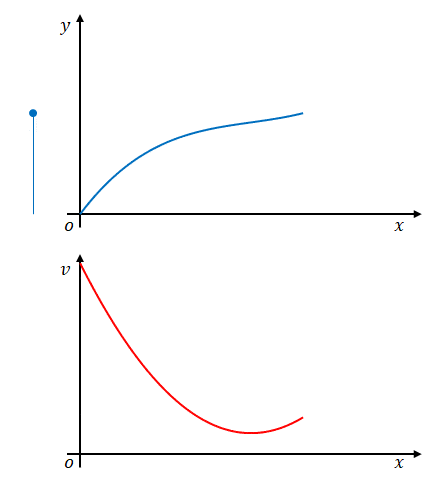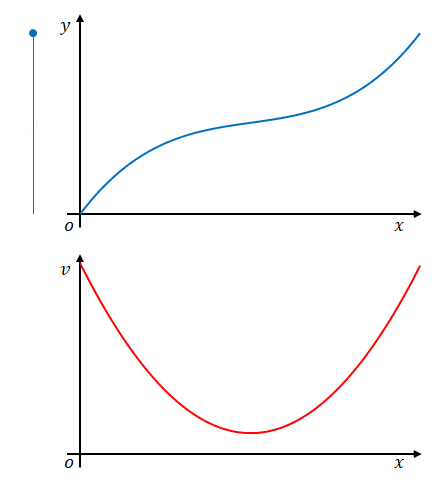
この場合、単純な割り算で求めることはできません。
そこで下の図のように\(x\)を複数の区間に分け、それぞれの区間では一定の速度で動いていたとみなせばどうでしょう。
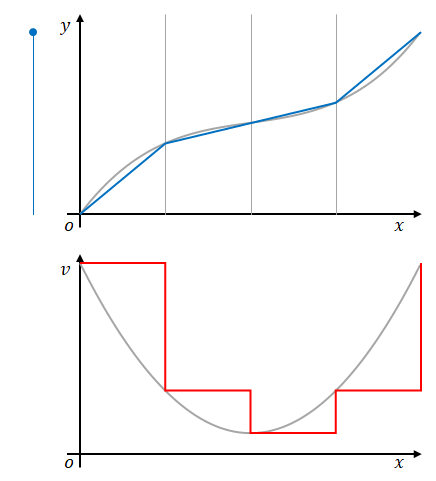
これであればそれぞれの区間で割り算を使うことにより求めることができます。
もちろんこれでは誤差があります。
では、この区間を小さくしたらどうでしょう。
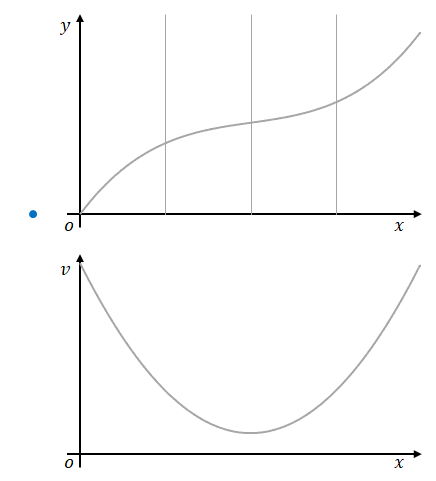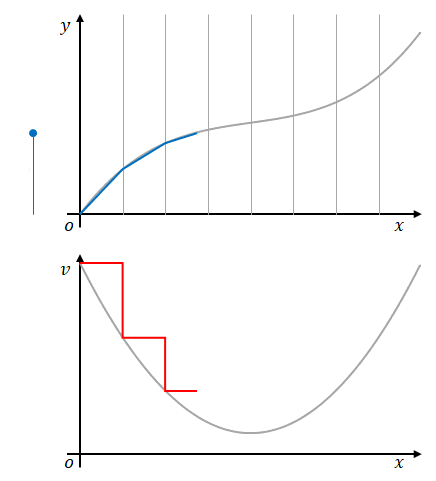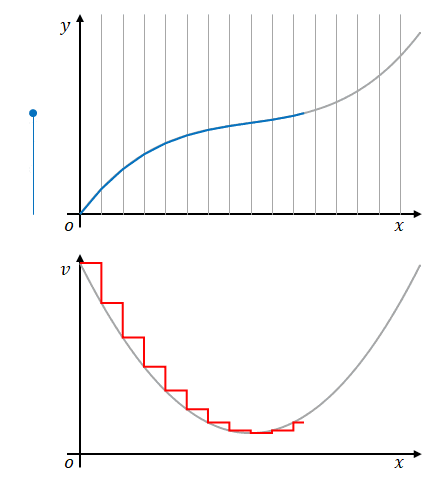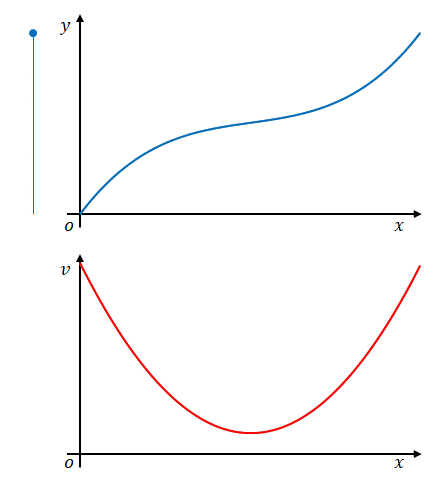
誤差は小さくなるはずです。
しかし近似であることには変わりありません。これで速度は求められるといえるのでしょうか。
区間を小さくしていくにつれ、誤差はどうなるでしょう。小さくなりますね。区間を無限に小さくすると誤差も無限に小さくなります。したがって、この方法で速度は求められるはずです。

2 微分の定義
前章では一定ではない速度を位置と時間から求める方法を考えました。本章ではこれを数式で表すことを考えましょう。
まず、\(y\)と\(v\)を以下のように関数で表すことにします。どの時間における位置や速度であるかをわかるようにするためです。
$$f(x)=y$$
$$f'(x)=v$$
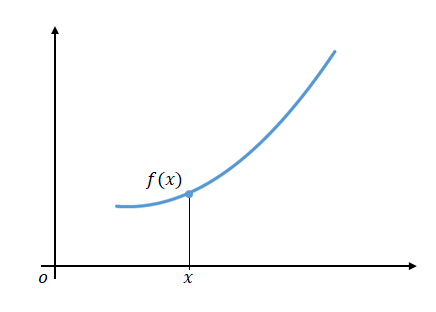
さて、速度を求めるためには、それぞれの区間で一定の速度で移動しているものとするのでした。そこで一つの区間についてその速度を関数と\(x\)で表します。
区間の開始時刻を\(x\)、その時の位置を\(f(x)\)とします。
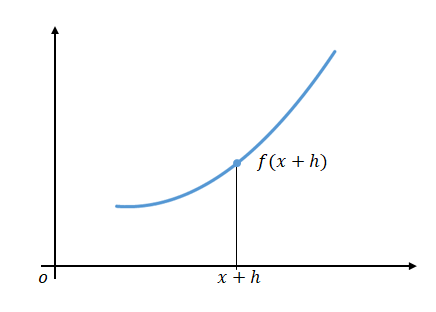
その区間での経過時間を\(h\)とすると、区間の終了時刻は\(x+h\)、その時の位置は\(f(x+h)\)です。
グラフ上、この\(2\)点を結ぶ直線が一定の速度で移動していることを表します。
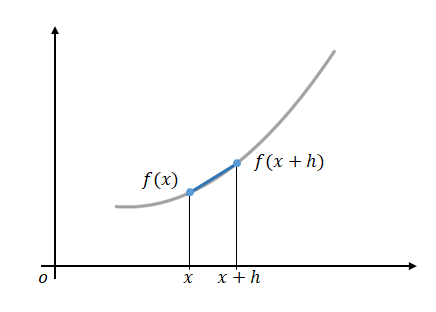
したがって、この傾きが速度です。傾きは2点の座標から、
$$\frac{f(x+h)-f(x)}{(x+h)-h}=\frac{f(x+h)-f(x)}{x}$$
と表されます。
区間の間隔が有限であれば誤差を含むので、\(h\)を無限に小さくするため、極限の
$$\lim_{h\rightarrow 0}$$
を用い
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$
と表します。これが誤差のない速度、つまり微分を表しています。
3 まとめと補足
・微分とは、変数の変化に対する関数の変化の割合を表すことです。
・例えば、その関数が\(f(x)\)と表される場合、「\(x\)で微分する」あるいは「\(x\)について微分する」といいます。
・微分した関数のことを導関数とよびます。
・微分の記法には複数の発案者がいますが、代表的なものは以下です。
ライプニッツ:
\begin{array}{ccc}
\displaystyle \frac{d y} {dx} & \displaystyle \frac{d \left(f(x)\right)}{dx} & \displaystyle \frac{d}{dx}f(x)
\end{array}
ラグランジュ:
\begin{array}{ccc}
y’ & f'(x)
\end{array}
・ある関数を\(1\)度微分した導関数を、回数を明示してよぶ場合は\(1\)階導関数と、「階」で表します。\(1\)階導関数を微分した関数は\(2\)階導関数とよびます。
・\(2\)階導関数は以下のように表します。
\begin{array}{ccc}
\displaystyle \frac{d^2 y} {dx^2} & f^{\prime\prime}(x)
\end{array}
・前述のように、微分とは、\(x\)の変化(増分)に対する\(f(x)\)の変化(増分)の割合なので、これを数式で表すと、
$$\frac{f(x)の増分}{xの増分}$$
ただし、\(x\)の増分は無限小でなければなりません。
したがって、\(x\)の増分を\(h\)とすると、微分は
$$f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$
と表すことができます。
