積分は「微分とは逆の概念」といえます。ただし、微分とは完全に逆というわけではありません。この「微分とは逆」という概念から出発し、その違いを踏まえながら積分とは何かを考えてみましょう。
0 概要
関数\(F(x)\)を\(x\)で微分した関数を\(f(x)\)とします。
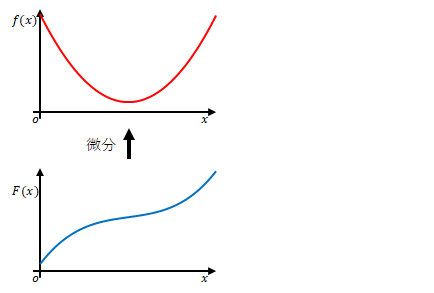
このページでは\(f(x)\)を積分すると何が得られるかを考えます。ただし、積分には大きく分けて\(2\)種類あります。1章と3章では不定積分、2章では定積分について述べます。
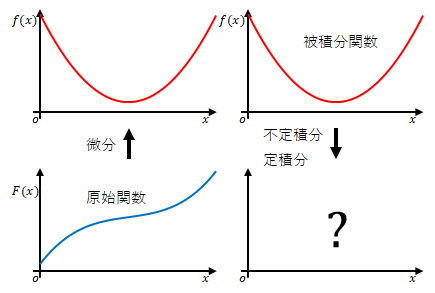
なお、微分をする際の元の関数(\(F(x)\))を原始関数、積分をする際の元の関数(\(f(x)\))を被積分関数とよびます。
1 不定積分(1)
微分をすると\(f(x)\)になる関数とはどのような関数でしょう。
当然\(F(x)\)を微分すると\(f(x)\)になりますね。
それだけでしょうか。
例えば、
$$F(x)+1$$
はどうでしょう。
やはり微分すると\(f(x)\)になりますね。\(1\)に限らず、あらゆる値の定数項があっても微分すると\(f(x)\)になります。
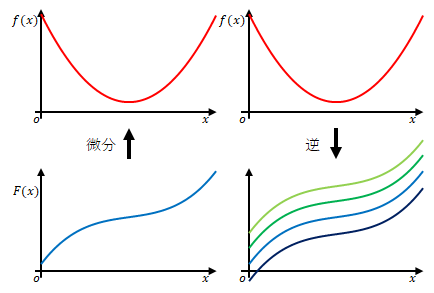
したがって定数項を\(C\)とし、微分をして\(f(x)\)になる式を
$$F(x)+C$$
と表すことができます。
この、微分すると被積分関数となる関数を求める演算が不定積分です。積分記号\(\displaystyle \int\)を用い、
$$\int f(x) dx$$
と表します。
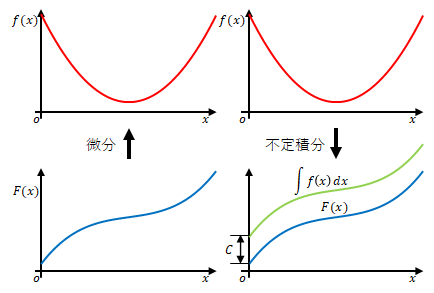
原始関数との関係は
$$\int f(x) dx=F(x)+C$$
となります。この\(C\)を積分定数とよびます。
2 定積分
1.1 原始関数の増分の累積
微分とは、関数の増分を微小な変数の増分で割ることにより、変化の割合を求めることでした。ここでは逆に変化の割合と変数の増分より関数の増分を求めることを考えます。
関数の増分を\(F(x+h)-F(x)\)、変数\(x\)の増分を\(h\)とすると、
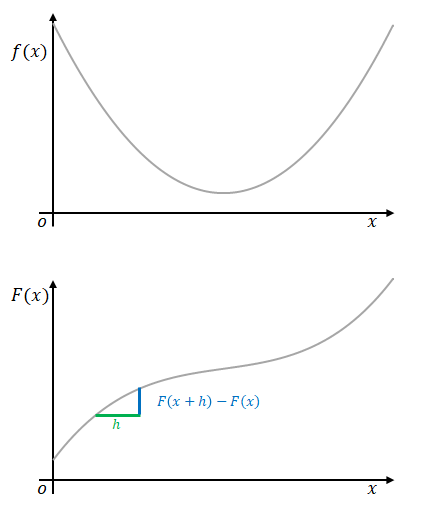
変化の割合は\(F(x+h)-F(x)\)を\(h\)で割った値であり、これが\(f(x)\)となるのでした。
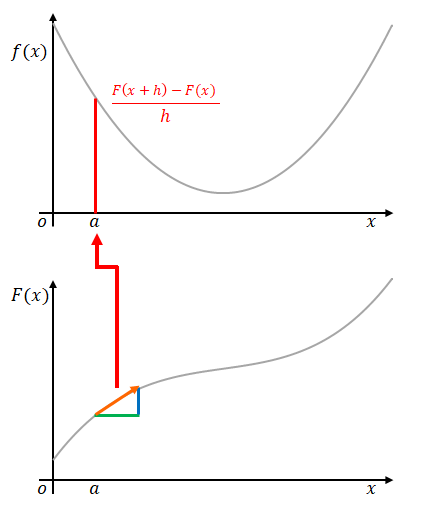
これを逆、つまり\(\displaystyle \frac{F(x+h)-F(x)}{h}\)に\(h\)を掛けることにより\(F(x+h)-F(x)\)が得られます。
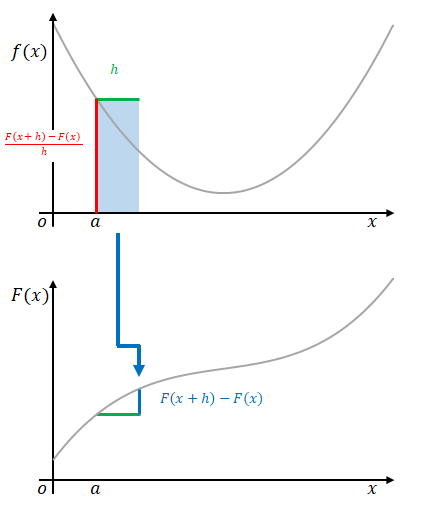
この区間を\(x=a\)から\(x=c\)までとすると、
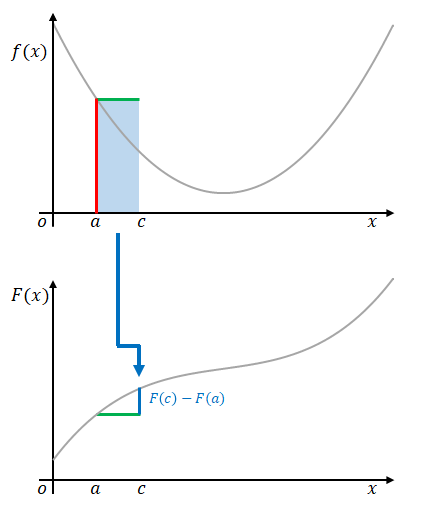
\(F(x+h)-f(x)\)は\(F(c)-F(a)\)と表すことができます。
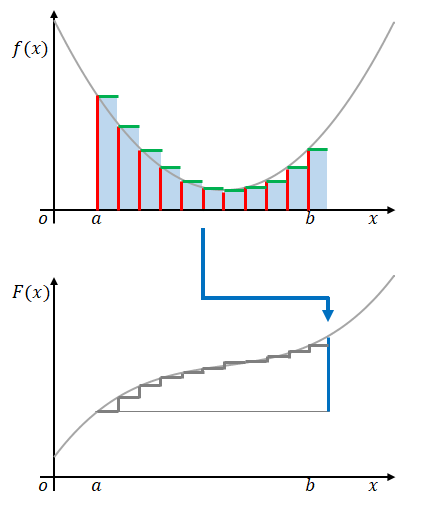
図では\(h\)を大きくしていますが、微分の定義では\(h\)は無限に小さい値でした。したがって\(F(c)-F(a)\)も無限に小さい値になり、これ単体では意味がありません。そこでこれらが複数集まるところを考えます。
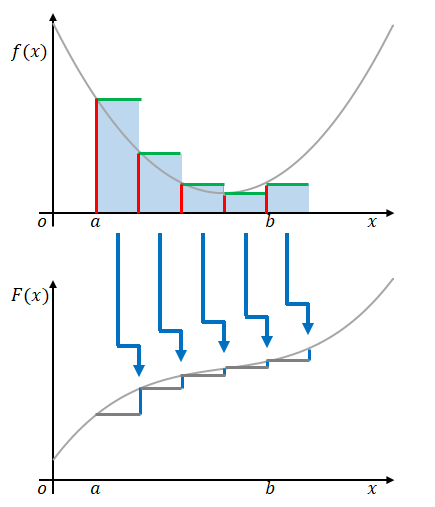
それぞれの区間の\(F(x+h)-F(x)\)の和を求めます。
この和には後述のような意味があるのですが、粗い区分では誤差を含みます。そこで微分のときと同じように、無限に小さい区間に分けます。
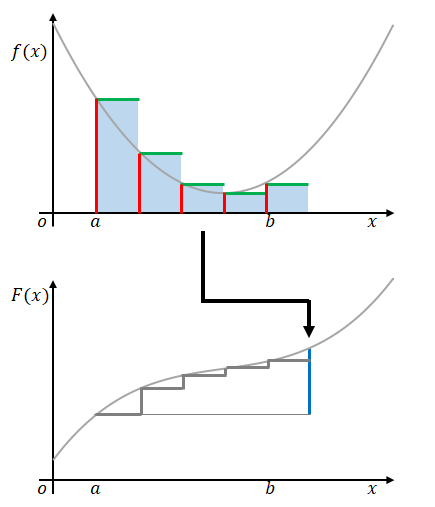
全区間の始点を\(x=a\)、終点を\(x=b\)とすると、青い線は2点間の原始関数の差\(F(b)-F(a)\)を示していることになります。
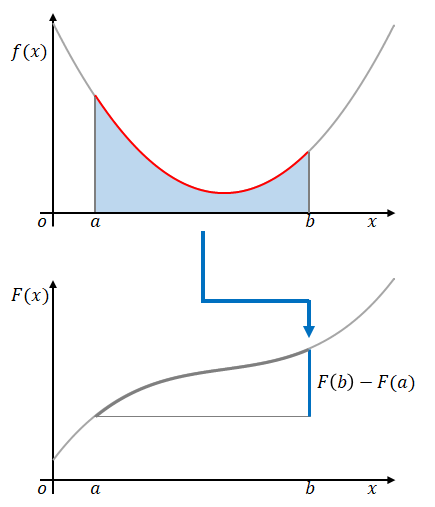
これを定積分とよびます。
式では以下のように表現します。
$$\int^{b}_{a}f(x)dx$$
1.2 計算方法
1.1節で、\(x=a\)から\(x=b\)までの定積分は\(F(b)-F(a)\)であると述べました。したがって定積分は不定積分の計算方法より求めることができます。つまり\(F(x)\)に\(x=a\)と\(x=b\)を代入したものがそれぞれの項です。
不定積分では積分定数の項がありましたが、定積分では\(2\)点間の原始関数の差なので、積分定数はありません。
確認しましょう。
$$\int f(x)dx=F(x)+C=G(x)$$
とおくと、
\begin{align}
\int^{b}_{a}f(x)dx &=G(b)-G(a) \\
&=\left(F(b)+C\right)-\left(F(a)+C\right)\\
\end{align}
\(x=a\)、\(x=b\)における\(C\)が同じ値であることから、
\begin{align}
\int^{b}_{a}f(x)dx &=F(b)-F(a)
\end{align}
となり、やはり積分定数は相殺されました。
つまり、定積分は、不定積分で得られる関数の変数に\(b\)と\(a\)を代入した値の差です。
例えば、
$$f(x)=2x$$
を\(1\)から\(2\)までの区間について積分するとします。
$$F(x)=x^2$$
なので、
$$\int^2_1 2x dx =\left[x^2\right]^2_1$$
を計算すればよいことになります。右辺は、鍵括弧内の変数に上の添え字を代入した値と下の添え字を代入した値の差を示しています。したがって、
$$\int^2_1 2x dx =\left[x^2\right]^2_1=2^2-1^2=5$$
となります。
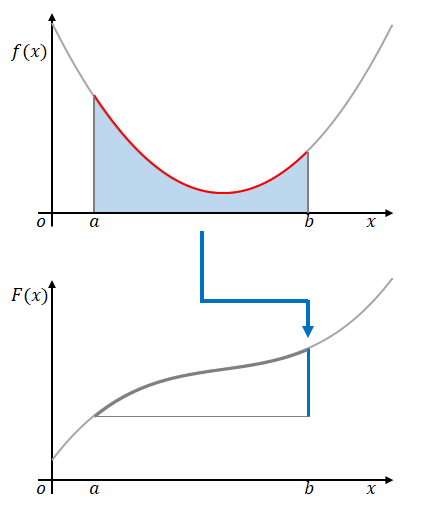
2.3 なぜグラフ上の面積が定積分になる?
改めて2.1節の図の一部を見てみましょう。
\(F(x+h)-F(x)\)は\(\displaystyle \frac{F(x+H)-F(x)}{h}\)(赤の線)と\(h\)(緑の線)の積でした。つまり、\(F(x+h)-F(x)\)はグラフでは青の線であると同時に水色の部分の面積でもあります。

したがって、これを無限に小さい複数の区間の集まりとすれば、やはり水色の部分の面積が\(F(b)-F(a)\)を示します。
つまり、グラフ上では被積分関数の線と積分区間で囲まれた部分の面積が定積分になります。

3 不定積分(2)
1章では、不定積分によって原始関数に積分定数が足された関数が得られると述べましたが、少し違った定義もできます。本章ではこの定義について述べます。
定積分は、与えられた範囲の両端における関数の値の差でした。例えばその範囲が\(a\)から\(b\)であれば定積分は\(F(b)-F(a)\)です。
では、定積分の区間を\(a\)から\(b\)までではなく、\(a\)から\(x\)までとしたらどうでしょう。\(a\)と\(b\)は定数でしたが、\(x\)は変数である点に注意してください。
定積分の結果は\(F(x)-F(a)\)ですね。したがって\(a\)が任意の定数であれば1章の不定積分の定義と同じになります。
改めて整理して考えましょう。
まず、積分区間と積分変数を区別するために積分変数を\(t\)、積分区間を\(t=a\)から\(t=x\)までとします。被積分関数は\(f(t)\)です。\(f(t)\)を\(t\)で積分するとその結果に\(t\)は残りませんが、積分区間として与えられた\(x\)と\(a\)は残ります。
下の図はそのイメージです。上側の図の横軸は\(t\)、下側の図の横軸は\(x\)です。
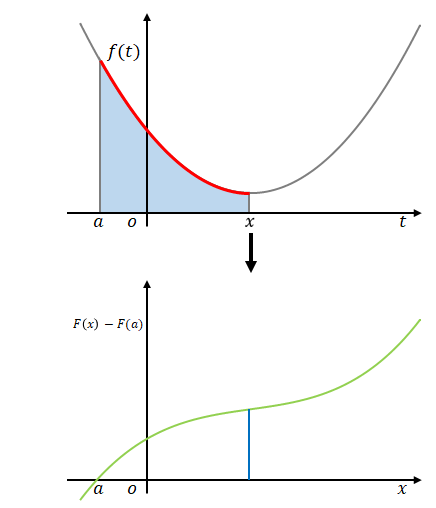
\(x\)が変わると積分区間が変わり、それによって定積分の結果も変わります。
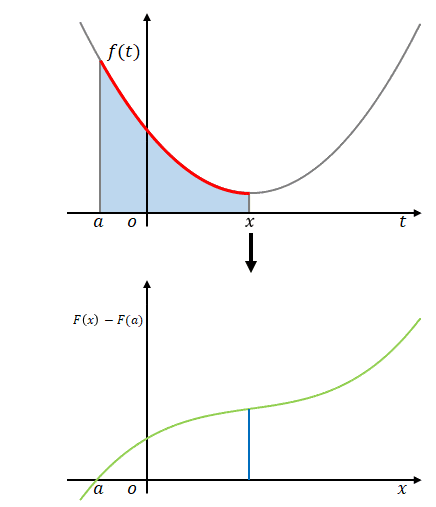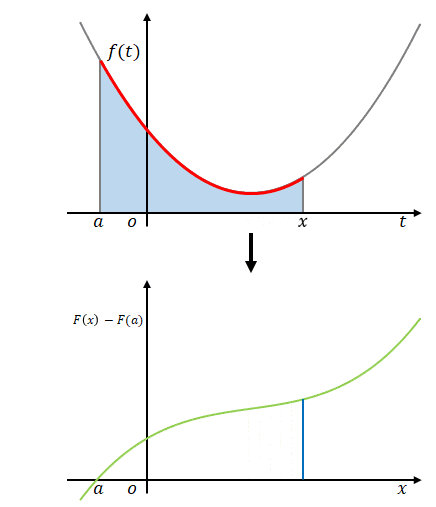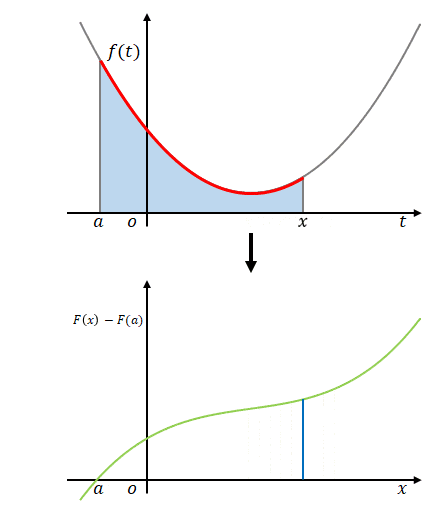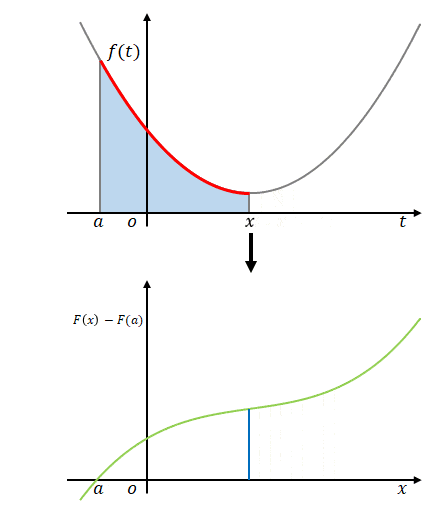
この定積分は、
$$\int^x_a f(t)dt=F(x)-F(a)$$
と表すことができます。
一方、1章では不定積分の結果を
$$\int f(x)dx=F(x)+C$$
としました。
上の2つの式を見比べてください。
\(C=-F(a)\)とすれば右辺は同じになります。
\(C\)は任意の定数でした。\(a\)も任意の定数であるということにすれば\(-F(a)\)も任意の定数なので\(C=-F(a)\)とすることができます。
したがって上の2つの式の左辺を等式で結び、以下のように不定積分を定義できます。
$$\int f(x) dx = \int^x_a f(t) dt$$

4 まとめ
\(F(x)\)を微分した関数を\(f(x)\)とし、この関数を積分することを考えます。
・\(F(x)\)を原始関数、\(f(x)\)を被積分関数とよびます。
・微分して\(f(x)\)となる関数を求めることを\(f(x)\)の不定積分とよび、
$$\int f(x)dx=F(x)+C$$
と表されます。
ただし\(C\)は任意の定数で、これを積分定数とよびます。
・ある\(2\)点について、原始関数の値の差を求めることを定積分とよびます。
これは、不定積分によって得られる\(F(x)\)を用いて\(F(b)-F(a)\)を計算することにより求められます。
・グラフ上では、\(x=a\)から\(x=b\)までの範囲について、\(f(x)\)と\(x\)軸で挟まれた図形の面積が定積分です。
・不定積分は、以下のように定積分によって定義することもできます。
$$\int f(x)dx=\int^{x}_{a} f(t) dt$$
ただし、\(a\)は任意の定数です。
