特殊相対性理論に関する、直観に反する性質の一つに「同時性の相対性」があります。ある慣性系から見ると同時に起きている事象が、別の慣性系では同時ではなくなるという現象です。なぜこのようなことが起きるのでしょう。
※本ページではミンコフスキー図と合わせてユークリッド空間(3次元の実空間)を図で表しています。現象に関係がある座標は\(x\)軸、\(x’\)軸だけですが、見やすくするために奥行方向(\(y\)、\(y’\))、高さ方向(\(z\)、\(z’\))の座標軸も表示しています。
※時間の進み方や寸法は図によって多少異なります。ご了承ください。
1 光を放った場合(ローレンツ変換)
1.1 \(S’\)から見た場合
慣性系\(S\)から見ると右に移動する電車があります。この慣性系を\(S’\)とします。電車の中央から左右の壁に向けて光を発しました。
下は\(S’\)から見たところを3次元とミンコフスキー図で表しています。
ユークリッド空間では、\(S’\)を固定して見ているので\(S\)の座標(青)は左へ移動しています。
ミンコフスキー図は\(ct’\)と\(x’\)を垂直に交わるように描いています。\(S’\)から見ると\(x\)軸は負の速度で移動しているので\(ct\)軸は左、\(x\)軸は下に傾きます。

\(S’\)から見ると、当然この光は同時に左右の壁に到達します。
1.2 \(S\)から見た場合
下は\(S\)から見た図です。
3次元空間では\(S’\)の座標(赤)は右へ移動しています。
ミンコフスキー図は\(ct\)と\(x\)を垂直に交わるように描いています。\(S\)から見ると\(S\)は正の速度で移動しているので\(ct’\)軸は右、\(x’\)軸は上に傾きます。
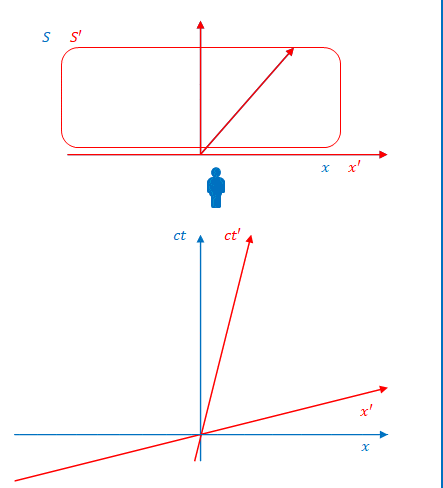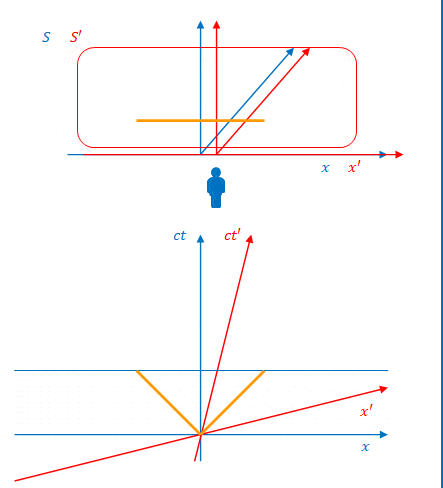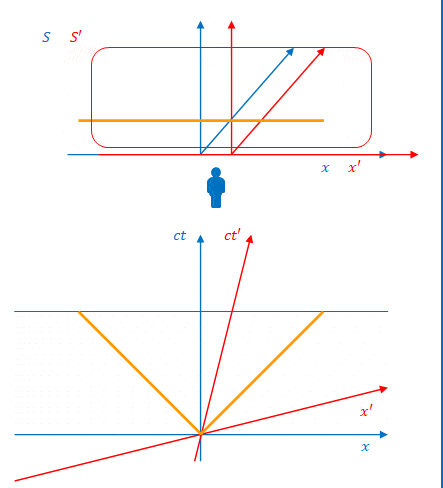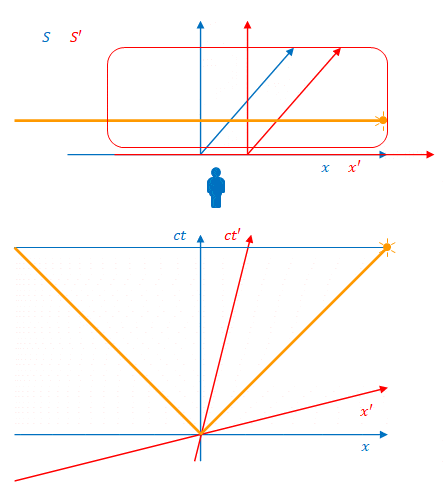
\(S\)から見ると光は先に左側の壁に到達し、その後で右側の壁に達しています。
つまり、ある慣性系から見ると複数の事象が同時に起きている(この場合は\(S’\)から見ると光が左右の壁に同時に到達する)にもかかわらず、別の慣性系から見ると同時ではない(\(S\)から見ると光が左右の壁に到達する時刻が同一でない)という現象が生じます。これを同時性の相対性(同時性の不一致)とよびます。
2 ボールを放った場合(ガリレイ変換)
前章との比較のため、光ではなく2個のボールを放った場合を、座標変換がガリレイ変換であるとして考えてみます。
2.1 \(S’\)から見た場合
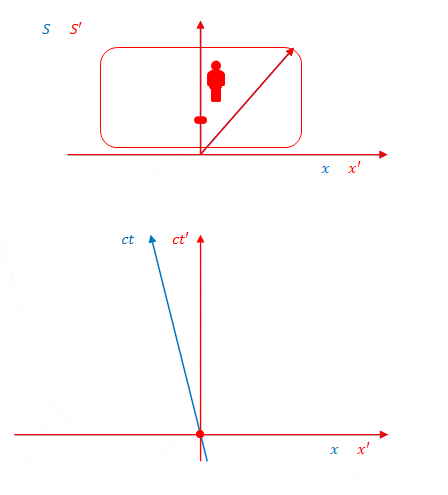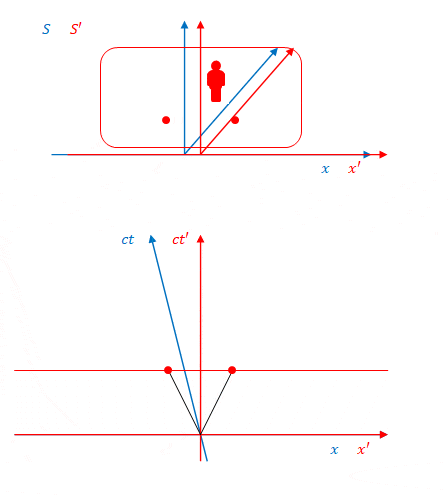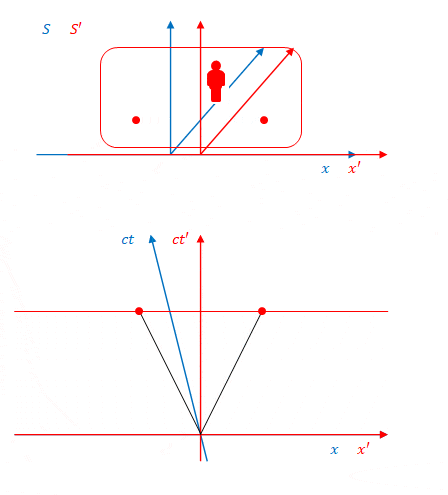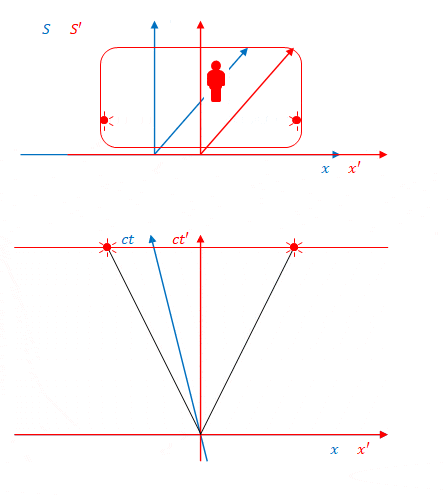
電車の中央から左右の壁に向けて同じ速度でボールを1個ずつ放ったとします。重力の影響は考えません。
下の図は\(S’\)から見た場合です。赤の丸がボールです。
ここで、ガリレイ変換の場合の時空図について補足します。
ガリレイ変換では時間の遅れとローレンツ収縮がないので時空図の\(x\)軸と\(x’\)軸は同じ方向です。
ただしローレンツ変換と同様、座標が移動するので\(ct\)軸と\(ct’\)は同一の方向にはなりません。
これも当然ではありますが、\(S’\)から見ると左右同時にボールが到達します。
2.2 \(S\)から見た場合
次に\(S\)から見た場合です。

前章では左右同時に光が到達しませんでしたが、この例では左右同時にボールが到達します。
3 なぜ光の場合は同時性が相対的になる?
3.1 光を放った場合
ではなぜ光の場合は同時性が相対的になるのでしょう。
下の図は前章の例を\(S’\)から見た場合です。
紫と緑の線は左右方向の光行距離です。両者は同じ長さです。
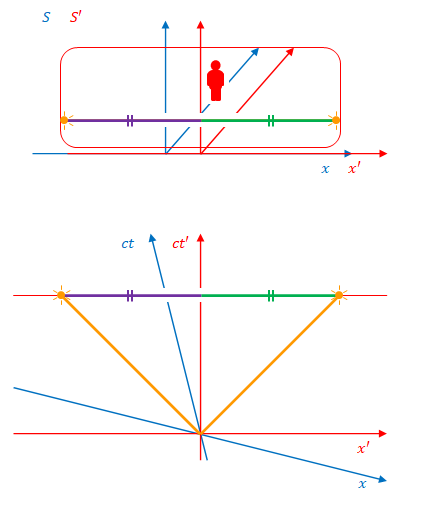
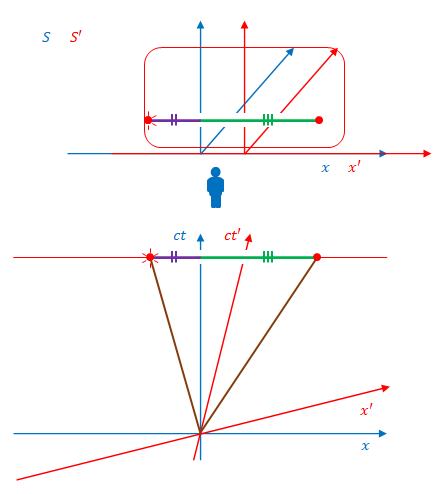
次の図は\(S\)から見た場合です。
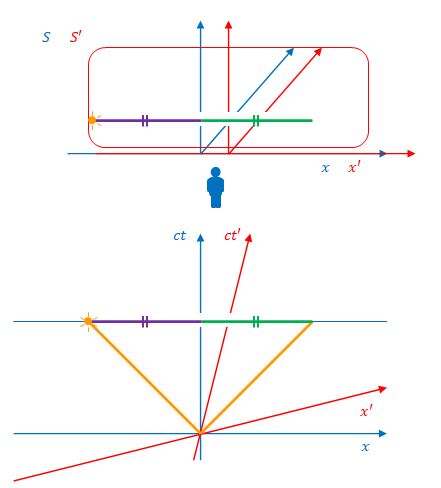
上の図は左側の壁に光が届いた瞬間ですが、右側の壁には届いていません。
さて、\(S’\)から見た場合と何が違うのでしょう。
電車の中心は移動しているのにもかかわらず、光の出発点は移動しないからですね。
比較のため、次節でボールを放った場合について考えましょう。
3.2 ボールを放った場合
下の図はボールを放ったときの様子を\(S\)から見た場合です。\(S’\)から見た場合については省略します。
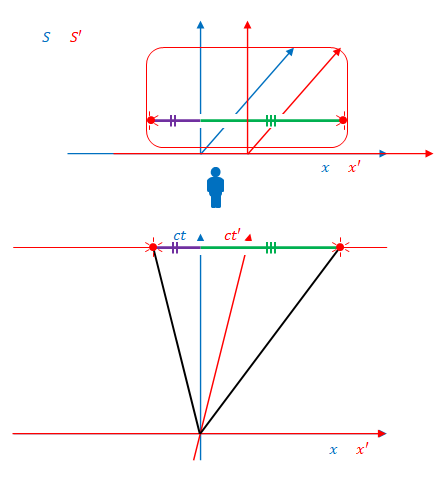
光を放った場合との違いは何でしょう。
光は\(S\)、\(S’\)どちらから見ても左右に同じ速さで進みます。
ボールも\(S’\)から見ると左右同じ速さで進みます。しかし\(S\)から見ると系間の相対速度が加算されます。右方向へ進むボールは速く、左方向へ進むボールは遅くなります。
つまり、光の場合は光速度不変の原理によって速度が決まるという違いがあるのです。
ただし、光を放った場合だけ、同時性が相対的になるというわけではありません。次節でそのことについて述べます。
4 ボールを放った場合(ローレンツ変換)
ここまで、光を放った場合とボールを放った場合を比較してきました。ただしボールを放った場合の座標変換はガリレイ変換でした。ではローレンツ変換によって座標が変換される場合、ボールを放つと同時性が一致するでしょうか。
まず速度の合成則(特殊相対性理論3(運動量))についておさらいです。
以下のように、慣性系\(T\)から見て速度\(\boldsymbol{u}\)で移動する物体があるとします。
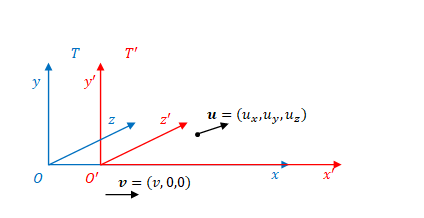
慣性系\(T’\)での速度は以下のように表されます。
$$u’_x = \frac {u_x – v } {1 – \frac {u_x v} {c^2} } $$
$$u’_y = \frac{u_y }{\gamma \left(1-\frac{u_x v}{c^2}\right)}$$
$$u’_z = \frac{u_z }{\gamma \left(1-\frac{u_x v}{c^2}\right)}$$
これが速度の合成則でした。
さて、本ページの電車の例では\(y\)、\(z\)の成分は\(0\)とします。
\(x\)に関する式の左辺を\(u_x\)にすると、
$$u_x = \frac {u’_x + v } {1 + \frac {u’_x v} {c^2} } $$
となります(過程は省略します)。
電車の例のボールの速度を以下のように定義します。
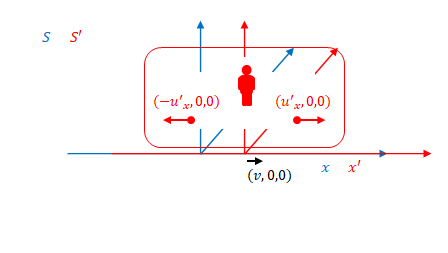
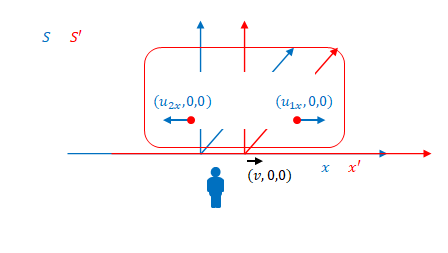
\(u_{1x}\)、\(u_{2x}\)は以下のように表されます。
$$u_{1x} = \frac {u’_x + v} {1 + \frac {u’_x v} {c^2} } $$
$$u_{2x} = \frac {-u’_x + v} {1 – \frac {u’_x v} {c^2} } $$
上の2式はローレンツ変換の場合です。
ガリレイ変換の場合は以下のように加算で表されます。
$$u_{1x} = u’_x + v $$
$$u_{2x} = -u’_x + v $$
さて、ガリレイ変換とローレンツ変換ではどちらが速いでしょう。
右方向の移動についてはガリレイ変換、左方向はローレンツ変換ですね。
したがって、ローレンツ変換では、ボールが左の壁に到達したとき、右の壁にはまだ到達していません。
下の図は光、ボール(ガリレイ変換)、ボール(ローレンツ変換)の軌跡をミンコフスキー図上で並べたものです。
傾きが小さいほど速度が大きいことを示しています。ローレンツ変換の場合、\(S\)から見た速度はガリレイ変換とは同一にはなりません。
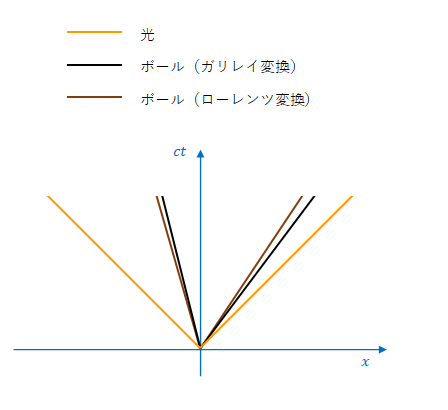
以上より、ローレンツ変換では同時性は相対的であるといえます。
5 まとめ
・ある慣性系では複数の事象が同時に起きているにもかかわらず別の慣性系では同時ではない場合があります。これを同時性の相対性(同時性の不一致)とよびます。
・電車の車両の中央から両側の壁に向かって光を放つと、電車の中の観測者は両側の壁に同時に到達したと認識しますが、外のプラットフォームにいる観測者は同時ではないと思います。これは光速度不変の原理によるものです。
・電車の中から光ではなくボールを両側に向けて放った場合、電車の中の観測者はやはり同時に両側の壁に到達すると判断します。ガリレイ変換の場合、プラットフォームにいる観測者も同時と判断しますが、ローレンツ変換の場合は同時ではないと認識します。これは座標変換の違いによるものです。
