テンソルの定義を正確に理解するのは容易ではありません。まず説明に出てくる用語を理解するところから始めなければならないかもしれません。また、分野によって定義が異なり、人によっても表現が異なるのですべてを理解するのは大変だと思います。ここではテンソルの定義は述べませんが、特殊相対性理論でよく使われるテンソルに関する事柄について簡単に話します。
1 テンソル
1.1 階数
テンソルは要素からなります。要素の数に制約はありません。
また、テンソルには階数という概念があります。要素の数が1の場合は0階(階数0)です。以下がその例です。
$$a$$
要素が複数存在する場合は並んでいると考えます。それが1行であれば1階です。
\begin{pmatrix}
a^0 & a^1 & a^2 & a^3
\end{pmatrix}
複数の行からなる場合は2階です。
\begin{pmatrix}
a^{00} & a^{01} & a^{02} & a^{03}\\
a^{10} & a^{11} & a^{12} & a^{13}\\
a^{20} & a^{21} & a^{22} & a^{23}\\
a^{30} & a^{31} & a^{32} & a^{33}
\end{pmatrix}
さらに高階のテンソルを定義することもできます。
1.2 2階テンソルの例
2階テンソルの例として、応力テンソルについて考えてみましょう。応力とは物体内部に生じる力のことです。
微小な立方体の表面に応力がはたらいているとします。
ある面に注目します。この面の応力は、面に垂直な成分(1方向)と面に接する成分(2方向)の計3種類からなると考えることができます。
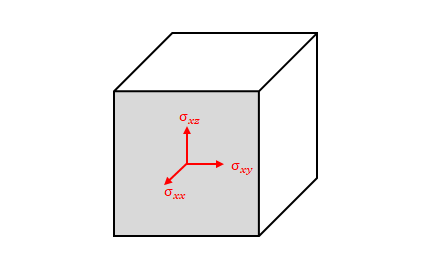
向かい合う面の垂直成分は大きさが釣り合っていると考え符号が逆になります。また、面に接する成分はせん断力という、捻じ曲げるような力なので点対称とします。つまり向かい合う面の面に接する2方向の力も符号が逆です。したがって向かい合う面の応力は省略します。
立方体の表面全体としては残りの面のうち2面について同様に定義できます。
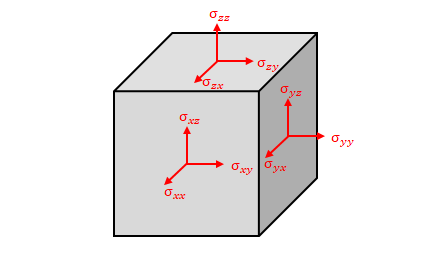
これら9種類の応力を以下のように表したものが応力テンソルです。
\begin{pmatrix}
\sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\
\sigma_{yx} & \sigma_{yy} & \sigma_{yz}\\
\sigma_{zx} & \sigma_{zy} & \sigma_{zz}
\end{pmatrix}
2 ローレンツ変換
ローレンツ変換の係数は行列で表すことができます。
以前にこのような式で表しましたが、
$$t^{\prime}=\gamma \left(t-\frac{vx}{c^2} \right)$$
$$x^{\prime}=\gamma (x-vt)$$
$$y^{\prime}=y$$
$$z^{\prime}=z$$
4元ベクトルを使うと
$$x’^0=\gamma \left(x_0-\frac{v x_1}{c} \right)$$
$$x’_1=\gamma \left (x_1- \frac {v x_0} {c} \right)$$
$$x’_2=x_2$$
$$x’_3=x_3$$
となります。\(x_0=ct\)、\(x’_0=ct’\)なので1番目の式は両辺に\(c\)を掛けています。
ここで、少し簡単にするためローレンツ因子\(\displaystyle\beta = \frac {v} {c} \)を使うと、1番目、2番目の式は
$$x’^0 = \gamma \left(x_0 – \beta x_1 \right)$$
$$x’^1 = \gamma \left(x_1 – \beta x_0 \right)$$
です。以上より、
$$
\begin{pmatrix}
x’^0 \\
x’^1 \\
x’^2 \\
x’^3
\end{pmatrix}
=\begin{pmatrix}
\gamma & -\beta \gamma & 0 & 0\\
-\beta \gamma & \gamma & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x^0 \\
x^1 \\
x^2 \\
x^3
\end{pmatrix}\\
$$
と表せます。
係数の行列を\(\Lambda\)とすると、
$$x’ ^ {\mu} = \Lambda ^{\mu} _ {\ \ \nu} x^{\nu}$$
の関係にあります。やや複雑にみえたローレンツ変換の式は4元ベクトルと\(\beta\)を使うと対称行列になることがわかりました。
逆に、\(x^{\mu}\)から\(x’^{\mu}\)への変換は
$$x ^ {\mu} = (\Lambda^{-1}) ^{\mu} _{\ \ \nu} x’^{\nu}$$
と表されます。
ただし、
$$
\Lambda^{-1}
=\begin{pmatrix}
\gamma & \beta \gamma & 0 & 0\\
\beta \gamma & \gamma & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
$$
です。導出過程は省略します。
\(\Lambda\)は座標変換をするためのものではありますが、これ自体が変換されるわけではありません。このようなものはテンソルとはよびません。したがって\(\Lambda\)はテンソルではなく行列です。
3 ミンコフスキー計量
相対性理論では反変ベクトル、共変ベクトルを互いへ変換することがあります。そのために使われるのがミンコフスキー計量です。
反変ベクトルから共変ベクトルへの変換は、
$$x’_{\mu} = \eta_{\mu \nu} x^{\nu}$$
と表されます。
ただし
$$
\eta_{\mu \nu}
=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & -1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & -1
\end{pmatrix}
$$
です。
同様に共変ベクトルから反変ベクトルへの変換は、
$$x’^{\mu} = \eta^{\mu \nu} x_{\nu}$$
ただし、
$$
\eta^{\mu \nu}
=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & -1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & -1
\end{pmatrix}
$$
です。
これら\(\eta_{\mu \nu}\)と\(\eta^{\mu \nu}\)をミンコフスキー計量とよびます。
両者の値は同じですが、上記のように意味が異なります。
式から明らかなように、ミンコフスキー計量は時間の符号は変えず、空間の符号を変えています。なぜ反変・共変への変換となるのでしょう。これについては別のページで説明する予定です。
前章の\(\Lambda\)は行列でしたが\(\eta_{\mu \nu}\)と\(\eta^{\mu \nu}\)はテンソルです。なぜこれらがテンソルなのか、については省略します。
