ここまでベクトルの要素は文字を添字として表記してきましたが、相対性理論では数字を添字とする表記が一般的です。また、それ以外にもいくつか見慣れない規則があると思います。簡潔に記述できて便利なのですが、はじめのうちは混乱するかもしれません。本ページでは添字に関する表記法について箇条書きにします。
※ここでは一般的な表し方を記載していますが、実際にはこの通りではない場合も多いので注意してください。
1.1 ベクトルの表し方
・ ベクトルを表す文字は太字にはせず小文字を用いることが多い。
特殊相対性理論6(4元ベクトル)では大文字を太字で表しましたが、相対性理論では一般的には小文字で通常の太さの字体を添字として使います。
・ベクトルには各要素を代表する意味で文字を付ける。
次の項の通り、ベクトルの各要素には整数を付けます。ベクトルにはこれらが存在することを示す意味で文字を使います。次節の例を確認ください。
・ベクトルの各要素に付ける添字は整数を用いる。
「特殊相対性理論6(4元ベクトル)」のページでは\(t\)、\(x\)、\(y\)、\(z\)を添字にしましたが、相対性理論では一般的には\(t\)→\(0\)、\(x\)→\(1\)、\(y\)→\(2\)、\(z\)→\(3\)を代わりに使います。
・各要素の添字が\(0\)から始まる場合はベクトルの添字にギリシャ文字、\(1\)から始まる場合はベクトルの添字にラテン文字(英語などのアルファベット)を使うことが多い。
例えば、要素の添字が\(\{1,2,3\}\)の場合はベクトルの添字に\(i\)、要素の添字が\(\{0,1,2,3\}\)の場合はベクトルの添字に\(\mu\)などを用います。
・反変ベクトルの場合、右上、共変ベクトルの場合右下に添字を付ける。
右上に添字が付くと、べき乗と間違えやすいので注意してください。
1.2 ベクトルの例
・3次元位置ベクトル(反変ベクトルの場合)
$$x^{i}=(x^1, x^2, x^3)$$
・4元速度(反変ベクトルの場合)
$$u^{\mu}=( u^0, u^1, u^2, u^3)$$
・4元運動量(共変ベクトルの場合)
$$p_{\nu}=(p_0, p_1, p_2, p_3)$$
1.3 2階テンソルの表し方
テンソルの概要については次のページで述べます。ここでは2階テンソルとは、行列のような2次元の配列だと考えてください。
・添字を2つ付ける。左側の添字は縦の変化、右側の添字は横の変化を表す。
次節の例を確認ください。
・2階反変テンソルは2つの添字を上、2階共変テンソルは2つの添字を下、混合テンソルは1つの添字を上、1つの添字を下につける。
ここでは名前だけ覚えてください。それぞれのテンソルの意味については省略します。
・小文字だけではなく大文字も使う。
1.4 2階テンソルの例
・2階反変テンソル
$$a^{\kappa\lambda}
=\begin{pmatrix}
a^{00} & a^{01} & a^{02} & a^{03}\\
a^{10} & a^{11} & a^{12} & a^{13}\\
a^{20} & a^{21} & a^{22} & a^{23}\\
a^{30} & a^{31} & a^{32} & a^{33}
\end{pmatrix}$$
・2階共変テンソル
$$b_{\xi\omicron}
=\begin{pmatrix}
b_{00} & b_{01} & b_{02} & b_{03}\\
b_{10} & b_{11} & b_{12} & b_{13}\\
b_{20} & b_{21} & b_{22} & b_{23}\\
b_{30} & b_{31} & b_{32} & b_{33}
\end{pmatrix}$$
・混合テンソル
$$c^{\rho}_{\ \ \sigma}
=\begin{pmatrix}
c^{0}_{\ \ 0} & c^{0}_{\ \ 1} & c^{0}_{\ \ 2} & c^{0}_{\ \ 3}\\
c^{1}_{\ \ 0} & c^{1}_{\ \ 1} & c^{1}_{\ \ 2} & c^{1}_{\ \ 3}\\
c^{2}_{\ \ 0} & c^{2}_{\ \ 1} & c^{2}_{\ \ 2} & c^{2}_{\ \ 3}\\
c^{3}_{\ \ 0} & c^{3}_{\ \ 1} & c^{3}_{\ \ 2} & c^{3}_{\ \ 3}
\end{pmatrix}$$
上の添字との関係を明確にするため、下の添字を右にずらしています。
また、以下のように反変と共変が逆の場合もあります。
$$c_{\rho}^{\ \ \sigma}
=\begin{pmatrix}
c_{0}^{\ \ 0} & c_{0}^{\ \ 1} & c_{0}^{\ \ 2} & c_{0}^{\ \ 3}\\
c_{1}^{\ \ 0} & c_{1}^{\ \ 1} & c_{1}^{\ \ 2} & c_{1}^{\ \ 3}\\
c_{2}^{\ \ 0} & c_{2}^{\ \ 1} & c_{2}^{\ \ 2} & c_{2}^{\ \ 3}\\
c_{3}^{\ \ 0} & c_{3}^{\ \ 1} & c_{3}^{\ \ 2} & c_{3}^{\ \ 3}
\end{pmatrix}$$
1.5 アインシュタインの縮約記法
相対性理論では各要素の和を求めることが多いため、サメーション(\(\sum\))を省略します。これをアインシュタインの縮約記法などとよびます。便利な表し方ですが、慣れるまでは和であることに気づかないことがありますので注意してください。
・1つの項に同じ文字の添字が上下各1回(計2回)現れたときはそれらの和をとる。
和をとった部分はスカラーになります。
この添字を擬標(ダミー・インデックス)とよびます。和をとると、指標としての意味がなくなるからこうよぶのでしょう。
1つの項に上2回または下2回の同じ文字が現れた場合は次項で述べる自由標になると思いますが、この通りではない場合もあるので文脈から判断するべきでしょう。
・1つの項に同じ文字の添字が1回しか現れないときはそれらの和をとらない。
つまり、前節までの説明の通り、その文字は各要素を代表する意味になります。この添字を自由標(フリー・インデックス)とよびます。
・1つの項に3回以上同じ文字を使うことはできない。
1.6 アインシュタインの縮約記法の例
・自由標が2つある場合
$$a^\mu b^\nu = (a^0 b^0, a^1 b^1, a^2 b^2, a^3 b^3)$$
結果はベクトルになります。
・擬標が1組ある場合
$$a^\mu b_\mu = \sum_{\mu=0}^3 a^\mu b_\mu = a^0 b_0 + a^1 b_1 + a^2 b_2 + a^3 b_3 $$
和をとるので結果はスカラーになります。
・擬標が1組、自由標が1つある場合
\begin{align*}
a_\mu b^\mu c^\nu &= \sum_{\mu=0}^3 a_\mu b^\mu c^\nu \\
&= (a_0 b^0 + a_1 b^1 + a_2 b^2 + a_3 b^3)
\begin{pmatrix}
c^{0} \\
c^{1} \\
c^{2} \\
c^{3}
\end{pmatrix}\\ \\
\end{align*}
和をとった部分はベクトルの係数になります。
・擬標が2組ある場合
\begin{align*}
a^\mu b_\mu c^\nu d_\nu &=\sum_{\mu=0}^3 \sum_{\nu=0}^3 a^\mu b_\mu c^\nu d_\nu\\
&= (a^0 b_0 + a^1 b_1 + a^2 b_2 + a^3 b_3) (c^0 d_0 + c^1 d_1 + c^2 d_2 + c^3 d_3)
\end{align*}
\(\mu\)と\(\nu\)それぞれの\(0\)から\(3\)までの和の積となる点に注意してください。以下のような、\(\mu\)と\(\nu\)が同じ値の項だけの積和ではありません。
\begin{align*}
a^\mu b_\mu c^\nu d_\nu & \neq \sum_{\mu= \nu=0}^3 a^\mu b_\mu c^\nu d_\nu\\
&= (a^0 b_0 c^0 d_0 + a^1 b_1 c^1 d_1 + a^2 b_2 c^2 d_2 + a^3 b_3 c^3 d_3)
\end{align*}
・2階テンソルとベクトルの積
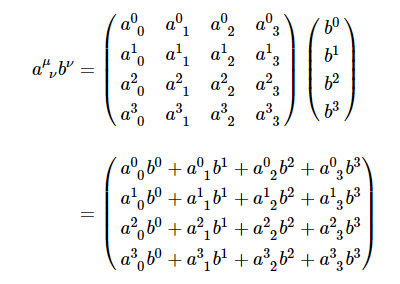
2階テンソルとベクトルの積を表す場合は、このように、テンソルの右側の添字とベクトルの添字を擬標とすることによってテンソルの積の演算規則と一致します。
また、演算をする前のベクトルが反変であれば演算後のベクトルも反変です。したがってこれを\(b’\)とすると、
$$b’^{\mu}=a^{\mu}_{\ \ \nu} b^{\nu} $$
と表されます。ベクトルが共変の場合は、
$$b’_{\mu}=a_{\mu}^{\ \ \nu} b_{\nu} $$
となります。
