前ページでは別の慣性系の時間の進み方と長さが変化することについて述べました。これらが変化するということはニュートン力学と整合していた座標変換を修正する必要があります。その一つが「ガリレイ変換」です。これに対し、特殊相対性理論においても物理法則を不変にするよう対応している座標変換が「ローレンツ変換」です。
本ページの目的はローレンツ変換の説明ですが、比較のためガリレイ変換についても述べます。
1 ガリレイ変換
下図のような3次元の直交座標系\(S\)を考えます。\(S\)は慣性系です。座標\(x_1, y_1, z_1\)に粒子があります。
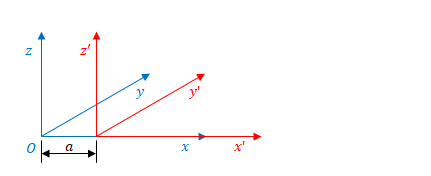
慣性系の座標系\(S^{\prime}\)を追加します。\(S\)との違いは原点が\(x\)方向に\(a\)だけ移動している点だけです。\(y\)方向、\(z\)方向の位置は同じです。全方向の縮尺も同じです。ここでは\(S^{\prime}\)は\(S\)から見て静止しています。
上記の粒子の座標は\(S^{\prime}\)ではどのように表されるでしょう。
\(x_1^{\prime}\)は\(x_1\)に比べて\(a\)だけ短くなっています。また、定義より\(y^{\prime}\)、\(z^{\prime}\)軸方向の縮尺と位置は\(y\)、\(z\)軸方向と常に同じです。したがって、
$$x_1^{\prime} = x_1 – a$$
$$y_1^{\prime}=y_1$$
$$z_1^{\prime}=z_1$$
です。
次に、\(S\)から見て\(S^{\prime}\)が速度\(v\)にて\(x\)の正の方向に移動している場合を考えます。
ある時刻を\(t_1\)とすると、この瞬間、粒子の座標はどのように表されるでしょう。
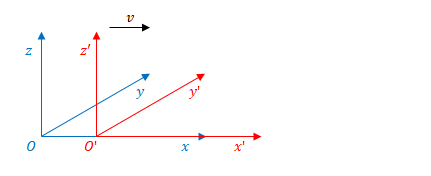
前述の\(a\)を\(vt_1\)に変更すればよいので、
$$x_1^{\prime} = x_1 – vt_1$$
$$y_1^{\prime}=y_1$$
$$z_1^{\prime}=z_1$$
となります。
一般化のため、以下のように\(x_1\)などの定数を\(x\)などの変数に置き換えます。また、慣性系によって時間の進み方は変わらないことを示す式を追加し、
$$t’ = t$$
$$x^{\prime} = x – vt$$
$$y^{\prime}=y$$
$$z^{\prime}=z$$
これが\(x\)方向に速さ\(v\)で\(S^{\prime}\)が移動する場合のガリレイ変換です。
ガリレイ変換は特殊相対性理論とは一致しない点に注意ください。
2 ローレンツ変換
ガリレイ変換では時間の遅れやローレンツ収縮は考慮されていません。つまり変換前後で時間と空間のスケールが変わりません。
これに対しローレンツ変換は特殊相対性理論が示す時間・空間の変化と一致します。
以下、2.1節、2.2節の2通りで光速度不変の原理からローレンツ変換を導きます。
両者とも以下を前提条件とします。
・慣性系\(S\)(下図青)の時間を\(t\)、慣性系\(S^{\prime}\)(下図赤)の座標を\(t^{\prime}\)とする。
・\(x, y, z\)と\(x^{\prime}, y^{\prime}, z^{\prime}\)の方向は一致している。
・\(S^{\prime}\)が\(x\)の正の方向へ速度\(v\)で移動している。
・\(t=0\)において\(t^{\prime}=0\)とする。
・\(t=0\)において\(S\)と\(S^{\prime}\)の原点は一致している。
ガリレイ変換では両慣性系の時間は共通でしたが、ローレンツ変換では別に定義している点に注意してください。

以下、全て観測者は慣性系\(S\)において静止しているものとします。\(S^{\prime}\)の時間や位置も\(S\)から観測した値です。
2.1 連立方程式を使った導出
\(t=0\)に、原点よりある方向へ光が照射されたとします。
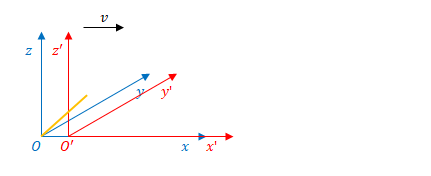
下の図は座標系\(S\)から見た光です。光の先端の座標を\( (x,y,z) \)とします。原点から光の先端までの距離は\(ct\)です。
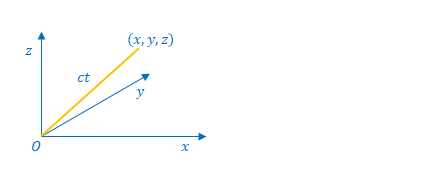
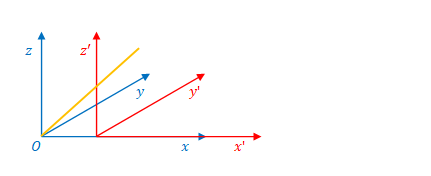
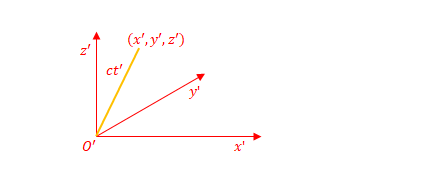
同じ光を座標系\(S^{\prime}\)から見ると下の図のようになります。
前ページの時間の遅れの例と似ていますが、\(S’\)から見た光は、移動方向と垂直と限定していない点に注意ください。
原点から先端までの距離は\(ct^{\prime}\)です。\(O\)と\(O^{\prime}\)の位置が異なるので、当然両者から光の先端までの距離は異なります。
しかし、光の速度\(c\)は変わりません(光速度不変の原理)。
慣性系によって光行距離が異なるにもかかわらず、光の速度は変わらないということは、時間が変わるということです。
また、時間が変わるために慣性系の移動方向の距離も変わります。
これらによって座標変換がいかに変わるかを確認します。
\(S\)における原点からの距離は以下のように表されます。
$$(ct)^2=x^2+y^2+z^2$$
\(S^{\prime}\)でも同じように表されるので、
$$(ct)^{\prime 2}=x^{\prime 2}+y^{\prime 2}+z^{\prime 2}$$
となります。
時間\(t\)の間速度\(v\)で\(S^{\prime}\)が右に進んでいるので、この距離の比を未知数\(A\)とすれば
$$x^{\prime}=A(x-vt)$$
です。
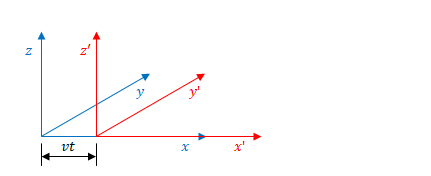
\(S^{\prime}\)の進行方向と垂直な方向はローレンツ収縮が起きないので、
$$y^{\prime}=y$$
$$z^{\prime}=z$$
です。
時間も進み方が変化するので\(x\)と\(t\)に未知の係数を追加し、
$$t^{\prime}=Bx+Dt$$
とします。
まとめると、
$$ct^2=x^2+y^2+z^2 \tag{1}$$
$$ct^{\prime 2}=x^{\prime 2}+y^{\prime 2}+z^{\prime 2} \tag{2}$$
$$x^{\prime}=A(x-vt) \tag{3}$$
$$y^{\prime}=y \tag{4}$$
$$z^{\prime}=z \tag{5}$$
$$t^{\prime}=Bx+Dt \tag{6}$$
ところで\((3)\)と\((6)\)は1次の項だけでよいのでしょうか。
また、\(y^{\prime}\)と\(y\)、\(z^{\prime}\)と\(z\)は等しいとしてよいのでしょうか。
これらは前ページの時間の遅れとローレンツ収縮より簡単に結論が得られますが、ここでは省略します。
この連立方程式を解くと、
$$A=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$
$$B=-\frac{\frac{v^2}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$$
$$D=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$
となります。
過程を確認する場合は「+」を押して展開してください。
したがって、
$$x^{\prime}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}(x-vt)$$
$$t^{\prime}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \left(t-\frac{vx}{c^2} \right)$$
両式の右辺の係数は頻繁に使われるので、
$$\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$
と置き、ローレンツ変換が得られます。\(y\)と\(z\)の関係式を追加し、
$$t^{\prime}=\gamma \left(t-\frac{vx}{c^2} \right)$$
$$x^{\prime}=\gamma (x-vt)$$
$$y^{\prime}=y$$
$$z^{\prime}=z$$
と表されます。
これがローレンツ変換です。
また、\(\gamma\)と同様に
$$\beta = \frac{v}{c}$$
もよく使われます。
\(\gamma\)や\(\beta\)をローレンツ因子とよびます。
2.2 時間の遅れとローレンツ収縮からの導出
前節では2つの慣性系における光行距離が等しいことからローレンツ変換を導きました。手順はわかりやすいのですが連立方程式を直観的に理解できる人はほとんどいないと思います。
本節では時間の遅れとローレンツ収縮が既知であるとしてこれらを座標に適用する方法を述べます。手順は多少ややこしくなりますが、連立方程式は不要なのでイメージはしやすいかと思います。
下の図のように、ある粒子の\(x\)座標の変換を考えます。
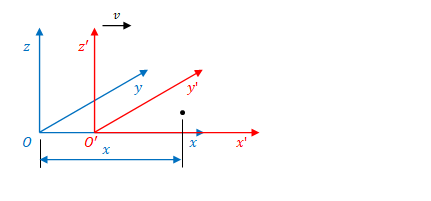
\(S\)の縮尺による\(S^{\prime}\)の移動距離は\(vt\)なので、\(O\)から\(O^{\prime}\)までの\(x\)方向の距離は\(vt\)、\(O^{\prime}\)から粒子までの距離は\(x-vt\)です。

この\(x-vt\)を\(S^{\prime}\)の縮尺で測った場合はローレンツ収縮により\(\gamma(x-vt)\)となります。\(\gamma\)はローレンツ因子(前節参照)です。
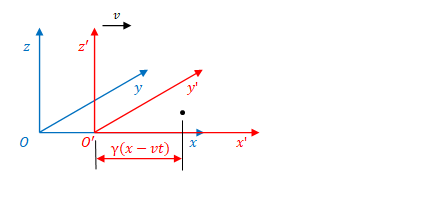
したがって以下の関係が得られます。
$$x^{\prime}=\gamma (x-vt)$$
次に、図のオレンジ色の線のように\(t=0\)において\(O\)、\(O^{\prime}\)から\(x\)方向へ光が放たれているところを考えます。

\(O\)から光の先端までの距離は\(x\)、\(O\)から\(O^{\prime}\)までの距離は\(vt\)です。

\(x\)を\(S\)における光行距離\(ct\)に置き換えることができます。また、\(t=\displaystyle \frac{x}{c}\)なので\(vt\)は\(\displaystyle \frac{vx}{c}\)に置き換えることができます。
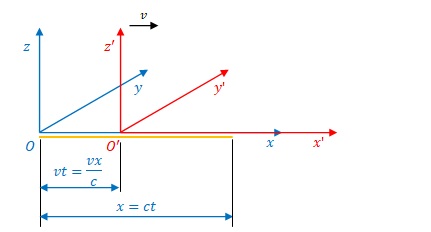
両者の差分にローレンツ収縮の\(\gamma\)を掛けて\(S^{\prime}\)における\(\displaystyle \gamma \left(ct-\frac{vx}{c} \right)\)が得られます。
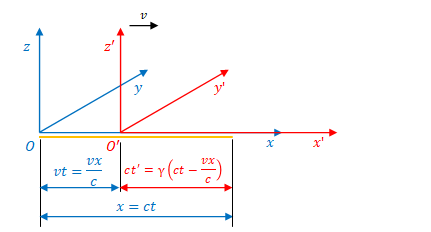
この値は\(S^{\prime}\)において光が進んだ距離\(ct^{\prime}\)と同じなので、
$$ct^{\prime}=\gamma \left(ct-\frac{vx}{c} \right)$$
したがって、
$$t^{\prime}=\gamma \left(t-\frac{vx}{c^2} \right)$$
となります。
2.3 ローレンツ収縮とローレンツ変換における係数の違い
ローレンツ収縮とローレンツ変換はどちらも空間の変化を表したものですが、記述の違いについて気になるところはないでしょうか。
ローレンツ収縮は
$$l=\frac {1} {\gamma} l_0$$
ですが、ローレンツ変換において\(t=0\)とすると、
$$x’=\gamma x$$
です。
\(l\)と\(x’\)、\(l_0\)と\(x\)が対応するはずです。しかし係数が逆数になっています。
なぜでしょう。
ローレンツ収縮は何らかの物体の長さが別の慣性系では収縮することを示しています。\(l_0\)と\(l\)はどちらも\(S\)から見て静止しているものさし(以下「\(S\)のものさし」)で測った値と考えればよいと思います。\(l\)は縮むので\(l_0\)より小さい値になります。
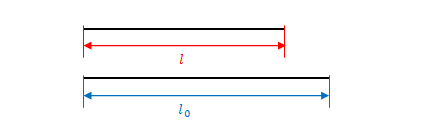
一方、ローレンツ変換は空間座標の変換です。\(x\)は\(S\)のものさし、\(x’\)は\(S’\)のものさしで測った値です。\(S’\)はものさしが縮むので\(x’\)は\(x\)より大きい値になります。

したがって、両者に矛盾があるわけではありません。
2.4 ローレンツ変換と時間の遅れにおける係数の意味の違い
同じように、時間の遅れとローレンツ変換についても確認してみましょう。
時間の遅れは下の式でした。
$$\Delta t’=\gamma \Delta t$$
ローレンツ変換の\(t’\)を求める式においても\(x=0\)とすれば同じ式になります。
$$t’=\gamma t$$
\(\Delta\)の有無の違いはありますが前節のような疑問はないように思えます。しかし、前節と同じように考えていくと両者の解釈は違うと考えられます。
時間の遅れはある事象から別の事象までの時間が慣性系によってどれだけ違うかを表したものです。この場合、\(\Delta t\)と\(\Delta t’\)はどちらも\(S\)の時計で測った値です。\(S’\)の時計のほうが進み方が遅いので\(\Delta t’\)のほうが長くなります。
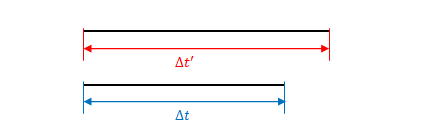
一方、ローレンツ変換は時間座標の変換です。\(t\)は\(S\)の時計、\(t’\)は\(S’\)の時計で測った値です。\(t’\)の時計のほうが進み方が遅いので、同じ座標に達するのにより時間がかかります(この後で補足します)。
これでそれぞれについて違いがあることがわかったように思えます。しかし、新たな疑問が生じます。前節と本節は同じような図であるのに両者の式における係数が異なっています。つまり前節では\(\gamma\)が逆数になっていましたが本節では逆数になっていません。
なぜ両者で式の関係が異なるのでしょう。
本節の説明で使った図について捕捉します。
ローレンツ収縮の説明に使った図の横方向は\(S\)の時計の進行速度に合わせて描いています。事象1と事象2の間の時間を比較すると、\(S’\)の時計は遅いので\(S’\)での事象2は右にずれています。
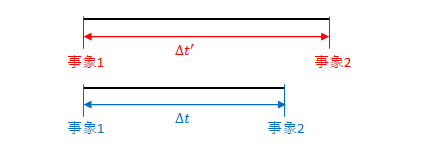
一方、ローレンツ変換の説明に使った図は2点間を移動する光の速度から求めた時間を示しています。2.2節のローレンツ変換での\(t’\)を求める手順を思い出してください。\(S\)上の2点間の距離を光速で割って時間を求めました。2点は固定です。速度も固定です。したがって、時計の進み方が遅いほど測った値は大きくなります。

3 まとめ
以下を前提条件とします。
・慣性系\(S\)の座標を\(x, y, z\)、慣性系\(S^{\prime}\)の座標を\(x^{\prime}, y^{\prime}, z^{\prime}\)とす・慣性系\(S\)の時間を\(t\)、慣性系\(S^{\prime}\)の座標を\(t^{\prime}\)とする。
・\(x, y, z\)と\(x^{\prime}, y^{\prime}, z^{\prime}\)の方向は一致している。
・\(S^{\prime}\)が\(x\)の方向へ速度\(v\)で移動している。
・\(t=0\)において\(t^{\prime}=0\)とする。
・\(t=0\)において\(S\)と\(S^{\prime}\)の原点は一致している。
この条件でローレンツ変換は以下のように定義されます。
$$t^{\prime}=\gamma \left(t-\frac{vx}{c^2} \right)$$
$$x^{\prime}=\gamma (x-vt)$$
$$y^{\prime}=y$$
$$z^{\prime}=z$$
ただし、
$$\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$
です。
