行列によって複数の数を\(1\)つの数(以後スカラー)のように扱うことができますが、スカラーでは成立する法則が行列でも同じように成立するとは限りません。このページではその中で交換法則と結合法則について確認します。
1 交換法則
\(a\)、\(b\)がスカラーであるとすると常に
$$ab=ba$$
が成立します。これが交換法則です。
しかし行列の場合、
$$AB=BA$$
は一般的には成立しません。
これを確認してみましょう。
下の図のように、\(A\)の\(1\)行目と\(B\)の\(1\)列目の積は\(1\)行目\(1\)列目の成分になります。
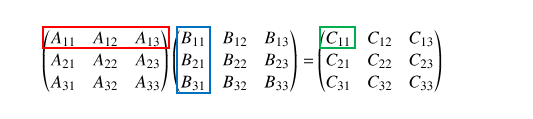
左と右を入れ替えてみます。
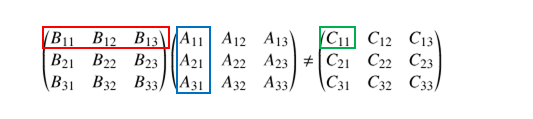
明らかに積の対象となる成分が異なるので一般的には積は同じにはなりません。
2 結合法則
\(a\)、\(b\)、\(c\)がスカラーの場合、
$$\left(ab\right)c=a\left(bc\right)$$
が成立します。
同様に、以下のように行列でも成立します。
$$\left(AB\right)C=A\left(BC\right)$$
確認するため、以下のような\(5 \times 5\)の行列\(3\)の積を考えましょう。
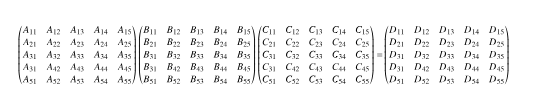
積の結果の中の\(1\)つの成分について考えます。ここでは\(2\)行目\(3\)列目とします。
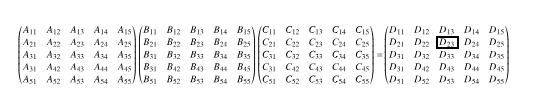
詳細は省略しますが、\(\left(AB\right)C\)の演算に関わる\(A\)、\(B\)、\(C\)の成分は以下です。

\(A\left(BC\right)\)の場合は以下です。

ここからは、左辺の各成分を点で表現し、
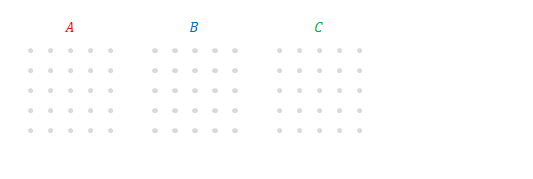
例えば\(A_{21}B_{13}C_{13}\)は下の図のように線で結ぶことにます。
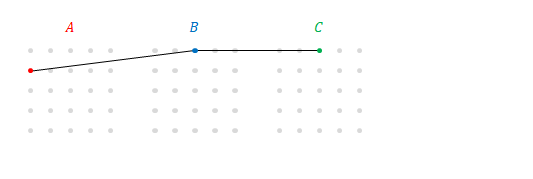
各行列の括弧は省略します。
では\(\left(AB\right)C\)について考えてみましょう。
その前に、\(AB\)はどう表されるでしょう。
\(A\)(の\(2\)行目)と\(B\)(の各列)の積は、以下の\(5\times5\)通りの積の和です。

次の図は下の段に\(AB\)と\(C\)(の\(3\)列目)との積を追加したところです。下段の\(5\)通りの積の和が\(\left(AB\right)C\)です。
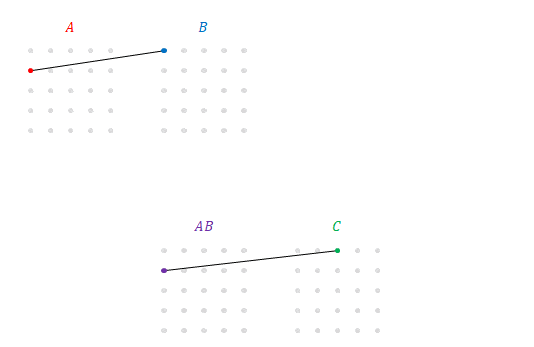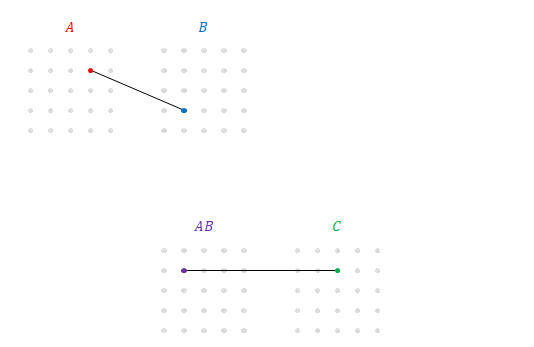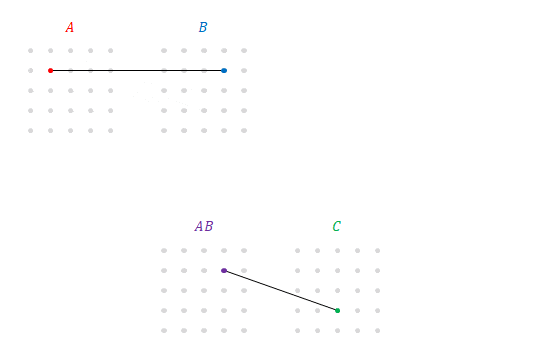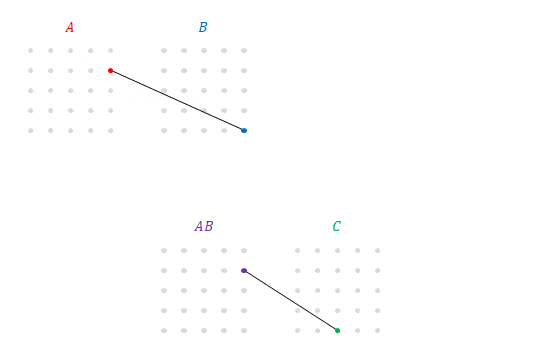
次の図は前の図の上段に線に、下段と同じ線を追加したところです。
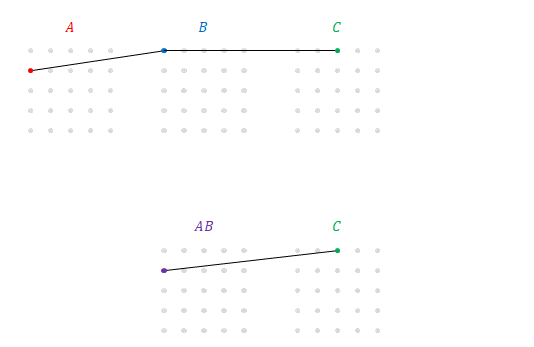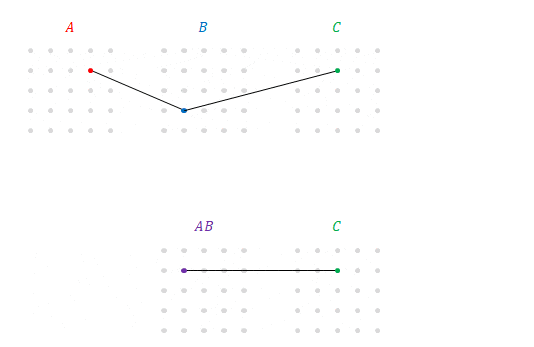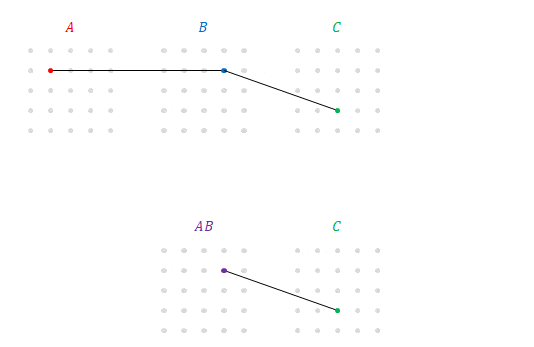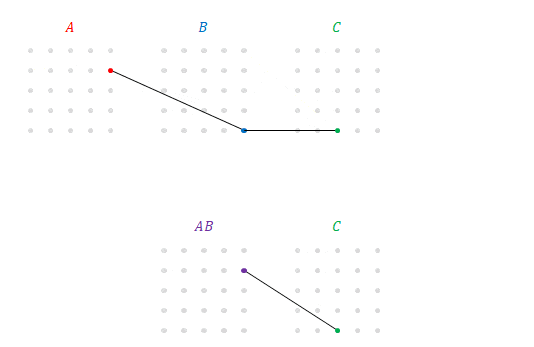
この上段の\(5\times5\)通りの積の和も下段と同じものを示しているので\(\left(AB\right)C\)です。
さて、上の図では\(B\)の積の対象が行方向優先で動いていました。
これを列方向優先に変えてみます。今比較したいのは各成分の積の和なので、表示を入れ替えても乗算の結果は変わりません。
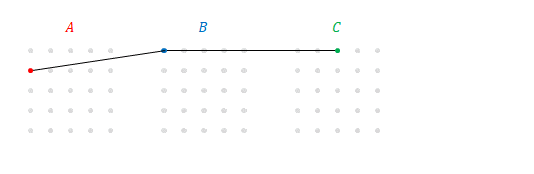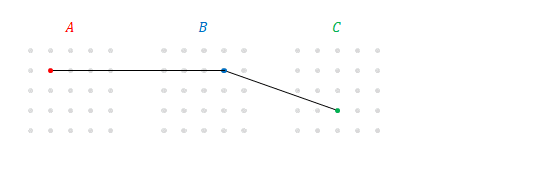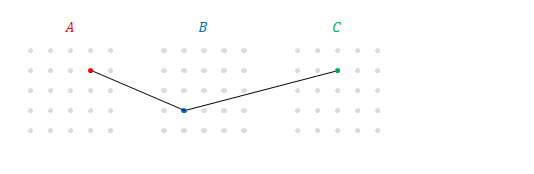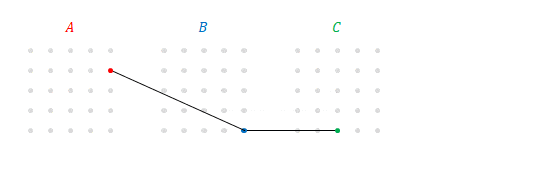
上の図の\(B\)と\(C\)に注目してください。これは\(B\)(の各行)と\(C\)(の\(3\)列目)の積ですね。
そこで次の図の下の段のように\(BC\)を表すことができます。これを\(A\)の各成分と結ぶと、\(A\)(の\(2\)行目)と\(BC\)(の\(3\)列目)の積であることがわかります。これはまさに\(A\left(BC\right)\)です。
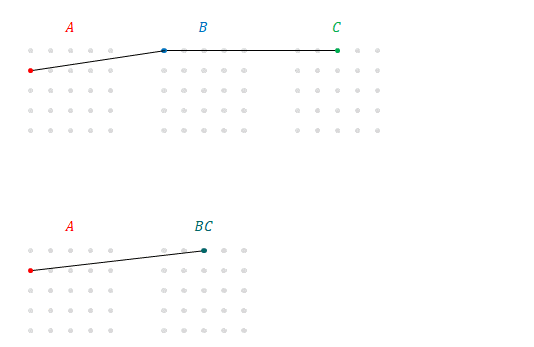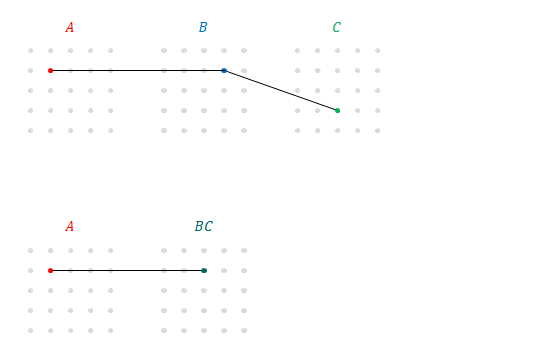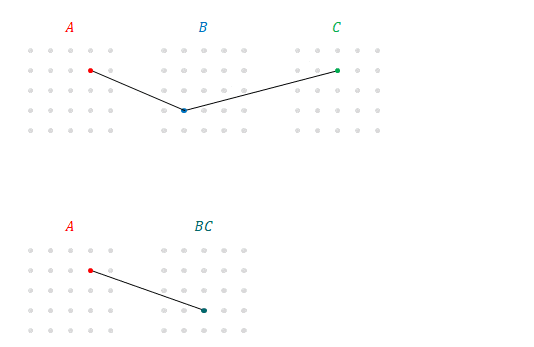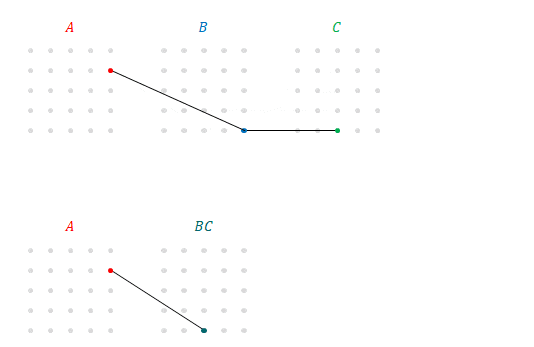
以上、\(\left(AB\right)C\)の成分ごとの積を順に表示してみたところ、その順序を入れ替えるだけで\(A\left(BC\right)\)の演算となりました。順序を入れ替えたところで行列の積としては変わりません。
以上は\(2\)行目\(3\)列目についての確認でしたが、明らかにどの行・列についても同様です。また、行と列の数を変えても同様です。
したがって行列でも結合法則が成立するといえます。
