行列とは？

投稿者: | 2023年7月15日
0件のコメント

高校の数学で扱う単元の中で行列が苦手だったという人は多いのではないでしょうか。その理由は、行列が何に使われるのか、どのような利点があるのかがわからないまま教わったからではないでしょうか。

例を見ながら、行列とは何か、行列を使う場合と使わない場合でどのような違いがあるか、を考えましょう。

1 生産数の例

問1.1

工場D、E、Fがある。ある日の、それぞれの\(1\)時間あたりの生産量とある日の稼働時間は下の表の通りである。その日の全体の生産量\(b_1\)はどれだけか。

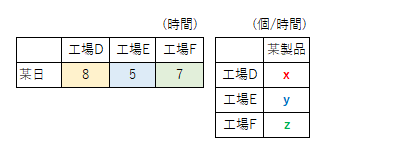
下の図は上記問題のイメージです。灰色の丸は製品を示しています。

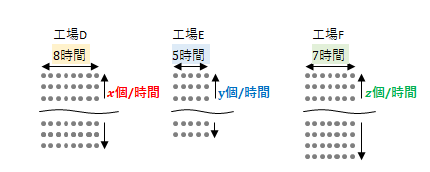
(a)行列を使わない場合

各工場の時間当たりの生産量と稼働時間を掛けて足し合わせます。

\begin{align}
b_1=8x+5y+7z
\end{align}

(b)行列を使う場合

以下のように、各工場の単位時間当たりの生産量と稼働時間をそれぞれ行列にして、その積として表します。

    \[ \begin{pmatrix} b_1 \\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7 \vspace{3pt} \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \\ \]

問1.2

工場D、E、Fがある。それぞれの\(1\)時間あたりの生産量と1日目から3日目までの稼働時間は下の表の通りである。1日目から3日目までのそれぞれの全体の生産量\(b_1-b_3\)はどれだけか。

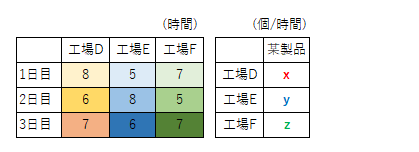
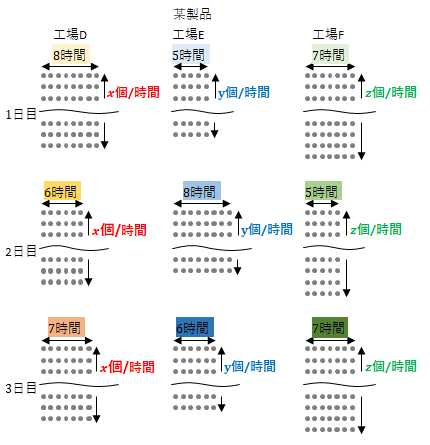
(a)行列を使わない場合

\(1\)日目から順に、

\begin{align}
b_1=8x+5y+7z\\
b_2=6x+8y+5z\\
b_3=7x+6y+7z
\end{align}

となります。

(b)行列を使う場合

上記式を個別に行列にすると、

    \[ \begin{pmatrix} b_1 \\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7\\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \]

    \[ \begin{pmatrix} b_2 \\ \end{pmatrix} = \begin{pmatrix} 6 & 8 & 5\\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \]

    \[ \begin{pmatrix} b_3 \\ \end{pmatrix} = \begin{pmatrix} 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \]

ですが、これらをまとめて、

    \[ \begin{pmatrix} b_1 \\ b_2 \\ b_3 \\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \]

と表すことができます。

つまり、積の右側の行列が共通であった場合、それらの左側の行をまとめることができます。

問1.3

工場D、E、Fがそれぞれ製品G、H、Iを生産する。それぞれの\(1\)時間あたりの生産量と1日目から3日目までの稼働時間は下の表の通りである。1日目から3日目までの製品G、H、Iそれぞれの全体の生産量\(b_{11}-b_{33}\)はどれだけか。

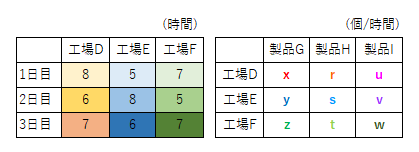
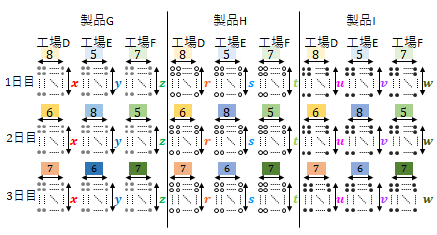
(a)行列を使わない場合

上から\(1-3\)日目、左から製品G-Hの順で表すと、

\begin{align}
b_{11}=8x+5y+7z\ \ \ \ \ \ \ \ b_{12}=8r+5s+7t\ \ \ \ \ \ \ \ b_{13}=8u+5v+7w\\
b_{21}=6x+8y+5z\ \ \ \ \ \ \ \ b_{22}=6r+8s+5t\ \ \ \ \ \ \ \ b_{23}=6u+8v+5w\\
b_{31}=7x+6y+7z\ \ \ \ \ \ \ \ b_{32}=7r+6s+7t\ \ \ \ \ \ \ \ b_{33}=7u+6v+7w
\end{align}

となります。

(b)行列を使う場合

各製品の\(1-3\)日分をそれぞれ行列で表すと、

    \[ \begin{pmatrix} b_{11}\\ b_{21}\\ b_{31}\\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix}\ \ \ \ \ \begin{pmatrix} b_{12}\\ b_{22}\\ b_{32}\\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} r \\ s \\ t \\ \end{pmatrix}\ \ \ \ \ \begin{pmatrix} b_{13}\\ b_{23}\\ b_{33}\\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} u \\ v \\ w \\ \end{pmatrix} \]

となりますが、各式の定数の行列（左側）が共通なので、これらをまとめて、

    \[ \begin{pmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33}\\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} x & r & u\\ y & s & v\\ z & t & w\\ \end{pmatrix} \]

と表すことができます。

つまり、積の左側の行列が共通であった場合、それらの右側の列をまとめることができます。

問1.4

工場D、E、Fがあり製品Eを生産している。それぞれの\(1\)時間あたりの生産量、\(1\)日目から\(3\)日目までの稼働時間、\(1\)日目から\(3\)日目までの生産量は下の表の通りである。\(x\)、\(y\)、\(z\)はどれだけか。

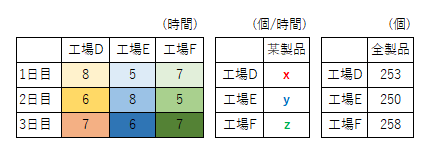
(a)行列を使わない場合

以下の連立方程式になるので、

\begin{align}
8x+5y+7z=253\\
6x+8y+5z=250\\
7x+6y+7z=258
\end{align}

これを解き、

\begin{align}
x=10\\
y=15\\
z=14
\end{align}

が得られます。

(b)行列を使う場合

行列を使うと以下のように表されます。

    \[ \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} = \begin{pmatrix} 253\\ 250\\ 258 \end{pmatrix} \]

スカラーであれば両辺を係数で割ることにより係数を移動させることができますが、行列には割り算と同等の概念はありません。しかし逆行列により割り算と似た演算ができます。

逆行列は以下のように定義されます。

    \[ \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix}^{-1} \end{pmatrix} \]

逆行列と自分自身の積は単位行列になります。

    \[ \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix}^{-1} \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix} \]

上の式の右辺が単位行列です。単位行列とはスカラーでいうところの\(1\)のようなもので、単位行列と任意の行列の積はその行列と同じです。

したがって、方程式の両辺に逆行列を掛けると、左辺は変数のみの行列となります。

    \[ \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix}^{-1} \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix} = \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix}^{-1} \begin{pmatrix} 253\\ 250\\ 258 \end{pmatrix} \]

    \[ \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix} = \frac{1}{3} \begin{pmatrix} 26 & 7 & -31\\ -7 & 7 & 2\\ -20 & -13 & -34\\ \end{pmatrix} \begin{pmatrix} 253\\ 250\\ 258 \end{pmatrix} \]

    \[ \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix} = \begin{pmatrix} 10\\ 15\\ 14 \end{pmatrix} \]

このように、連立\(1\)次方程式は行列を使って解くことができます。

※逆行列については別のページで説明する予定です。

また、

    \[ X= \begin{pmatrix} x\\ y\\ z \end{pmatrix} 、\ \ \ A= \begin{pmatrix} 8 & 5 & 7\\ 6 & 8 & 5\\ 7 & 6 & 7\\ \end{pmatrix} 、\ \ \ B=\begin{pmatrix} 253\\ 250\\ 258 \end{pmatrix} \]

とすると、

$$AX=B$$

の関係にあるので解は

$$X=A^{-1}B$$

と表されます。

このように、複数の数を文字で置き換えることにより簡潔に関係を表すことができる場合があります。

2 製品のシェアの例

問2.1

ある製品の\(0\)年度におけるシェアはX社が\(x_0\)、Y社が\(y_0\)であった。\(0\)年度から\(1\)年度にかけて、X社はY社の顧客を\(10\%\)を獲得しつつ、自社の顧客の\(80\%\)を維持した。Y社はX社の顧客を\(20\%\)得る一方、自社の顧客は\(90\%\)を維持した。\(1\)年度の両社のシェア\(x_1\)、\(y_1\)はどれだけか。

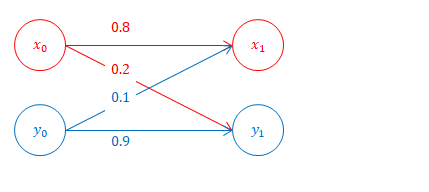
(a)行列を使わない場合

\(1\)年度のシェアは、

$$x_1=0.8x_0 + 0.1y_0$$

$$y_1=0.2x_0 + 0.9y_0$$

と表されます。

(b)行列を使う場合

上記を行列で表すと、

    \[ \begin{pmatrix} x_1\\ y_1\\ \end{pmatrix} \begin{pmatrix} 0.8 & 0.1\\ 0.2 & 0.9\\ \end{pmatrix} \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix} \]

となります。

問2.2

ある製品の\(n\)年度におけるX社のシェアが\(x_n\)、Y社のシェアが\(y_n\)であった。また、\(n-1\)年度から\(n\)年度にかけて、X社が自社の顧客を維持した割合は\(r_{xxn}\)、X社がY社から顧客を獲得した割合は\(r_{yxn}\)であった。Y社が自社の顧客を維持した割合は\(r_{yyn}\)、Y社がX社から顧客を獲得した割合は\(r_{xyn}\)であった。\(3\)年度の両社のシェア\(x_3\)、\(y_3\)を\(x_0\)、\(y_0\)の式で表せ。

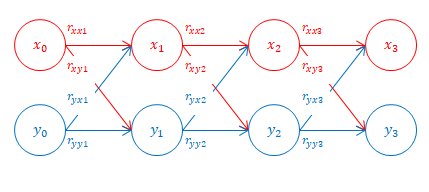
(a)行列を使わない場合

\(1-3\)年度のシェアは、前年度のシェアを用いて

\begin{align}
x_1&=a_{xx1} x_{0} + a_{yx1} y_{0}\\
y_1&=a_{xy1} x_{0} + a_{yy1} y_{0}\\
x_2&=a_{xx2} x_{1} + a_{yx2} y_{1}\\
y_2&=a_{xy2} x_{1} + a_{yy2} y_{1}\\
x_3&=a_{xx3} x_{2} + a_{yx3} y_{2}\\
y_3&=a_{xy3} x_{2} + a_{yy3} y_{2}\\
\end{align}

と表されます。

これらの式の\(x_1\)、\(y_1\)、\(x_2\)、\(y_2\)を消去すると、

\begin{align}
x_3&=a_{xx2} \left\{
a_{xx1} \left(a_{xx0} x_{0} + a_{yx0} y_{0}\right)
+ a_{yx1} \left(a_{xy0} x_{0} + a_{yy0}\right)\right\}\\
&+ a_{yx2} \left\{
a_{xy1}\left(a_{xx0} x_{0} + a_{yx0} y_{0}\right)
+ a_{yy1}\left(a_{xy0} x_{0} + a_{yy0}\right)
\right\}\\
y_3&=a_{xy2} \left\{
a_{xx1}\left(a_{xx0} x_{0} + a_{yx0} y_{0}\right)
+ a_{yx1} \left(a_{xy0} x_{0} + a_{yy0}\right)\right\}\\
&+ a_{yy2} \left\{
a_{xy1}\left(a_{xx0} x_{0} + a_{yx0} y_{0}\right)
+ a_{yy1}\left(a_{xy0} x_{0} + a_{yy0}\right)
\right\}\\
\end{align}

となります。\(x_0\)、\(y_0\)で分けて整理しても、

\begin{align}
x_3&=\left(a_{xx3} a_{xx2} a_{xx1} + a_{yx3} a_{xy2} a_{xx1} + a_{xx3} a_{yx2} a_{xy1} + a_{yx3} a_{yy2} a_{xy1} \right)x_0\\
&+\left(a_{yx3} a_{yy2} a_{yy1} + a_{xx3} a_{yx2} a_{yy1} + a_{xx3} a_{xx2} a_{yx1} + a_{yx3} a_{xy2} a_{yx1} \right)y_0\\
y_3&=\left(a_{xy3} a_{xx2} a_{xx1} + a_{yy3} a_{xy2} a_{xx1} + a_{yy3} a_{yy2} a_{xy1} + a_{xy3} a_{yx2} a_{xy1} \right)x_0\\
&+\left(a_{yy3} a_{yy2} a_{yy1} + a_{xy3} a_{yx2} a_{yy1} + a_{yy3} a_{xy2} a_{yx1} + a_{xy3} a_{xx2} a_{yx1} \right)y_0
\end{align}

と、あまりすっきりとした形にはなりません。

(b)行列を使う場合

行列を使う場合は、各年度のシェアは以下のように表すことができます。

    \[ $$ \begin{pmatrix} x_1\\ y_1\\ \end{pmatrix} = \begin{pmatrix} a_{xx1} & a_{yx1}\\ a_{xy1} & a_{yy1}\\ \end{pmatrix} \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix}\vspace{3pt}\\ \begin{pmatrix} x_2\\ y_2\\ \end{pmatrix} = \begin{pmatrix} a_{xx2} & a_{yx2}\\ a_{xy2} & a_{yy2}\\ \end{pmatrix} \begin{pmatrix} x_1\\ y_1\\ \end{pmatrix}\vspace{3pt}\\ \begin{pmatrix}x_3\\ y_3\\ \end{pmatrix} = \begin{pmatrix} a_{xx3} & a_{yx3}\\ a_{xy3} & a_{yy3}\\ \end{pmatrix} \begin{pmatrix} x_2\\ y_2\\ \end{pmatrix} $$ \]

これらをまとめると、

    \[ \begin{pmatrix} x_3\\ y_3\\ \end{pmatrix} = \begin{pmatrix} a_{xx3} & a_{yx3}\\ a_{xy3} & a_{yy3}\\ \end{pmatrix} \begin{pmatrix} a_{xx2} & a_{yx2}\\ a_{xy2} & a_{yy2}\\ \end{pmatrix} \begin{pmatrix} a_{xx1} & a_{yx1}\\ a_{xy1} & a_{yy1}\\ \end{pmatrix} \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix} \]

と、簡潔に表すことができます。

また、以下のようにおくと、

    \[ X_n= \begin{pmatrix} x_n\\ y_n\\ \end{pmatrix} 、\ \ \ A_n= \begin{pmatrix} a_{xxn} & a_{yxn}\\ a_{xyn} & a_{yyn}\\ \end{pmatrix} \]

上記式は、

$$X_3=A_3 A_2 A_1 X_0$$

と表すことができます。

3 回転による座標変換の例

問3.1

xy平面において座標\(\left(x,y\right)\)にある点を、原点を中心として角度\(\theta\)だけ回転移動させると、移動先の座標\(\left(x’,y’\right)\)はどう表されるか。

(a)行列を使わない場合

詳細は省略しますが、以下の関係になります。

\begin{align}
x’&=\cos \theta x – \sin \theta y\\
y’&=\sin \theta x + \cos \theta y
\end{align}

(b)行列を使う場合

行列を使う場合は、

    \[ \begin{pmatrix} x'\\ y'\\ \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta\\ \sin \theta & \cos \theta\\ \end{pmatrix} \begin{pmatrix} x\\ y\\ \end{pmatrix} \]

となります。

この右辺の左側の行列を回転行列とよびます。

問3.2

\(xyz\)空間において座標\(\left(x,y,z\right)\)にある点を、\(x\)軸を中心として角度\(\alpha\)、\(y\)軸を中心として角度\(\beta\)、\(z\)軸を中心として角度\(\gamma\)、だけ回転移動させると、移動先の座標\(\left(x^{\prime\prime\prime},y^{\prime\prime\prime},z^{\prime\prime\prime}\right)\)はどう表されるか。

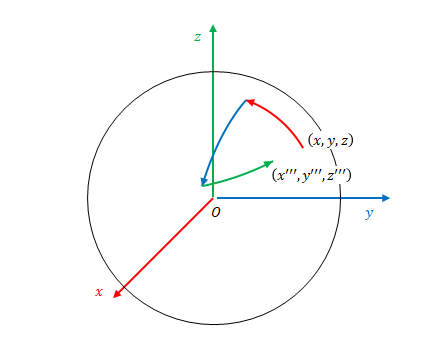
設問に「\(x\)軸を中心として\(\alpha\)だけ回転移動」とありますが、これは\(x\)軸を正から負の方向に見ると、反時計回りに\(\alpha\)だけ移動したという意味です。

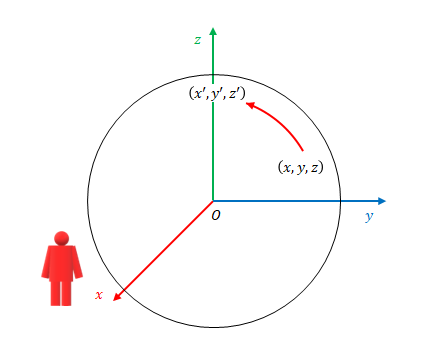
※図では移動後の座標値を\(\left(x’,y’,z’\right)\)としています。

(a)行列を使わない場合

\(x\)軸方向を向く観測者からは、\(yz\)平面で点が原点を中心として角度\(\alpha\)だけ回転しているように見えます。

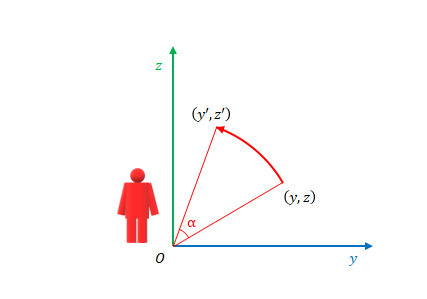
そこで、\(y’\)、\(z’\)と\(y\)、\(z\)の関係は、前問と同様に表されます。また、\(x\)は値を変えずに\(x’\)となり、\(y’\)、\(z’\)に影響を与えません。以上より、

\begin{align}
x^{\prime}&=x\\
y^{\prime}&=\cos \alpha y – \sin \alpha z\\
z^{\prime}&=\sin \alpha y + \cos \alpha z
\end{align}

と表されます。

\(y\)軸の周り、\(z\)軸の周りでの回転についても同様の式が得られます。過程は省略しますが、これらをまとめると、

\begin{align}
x^{\prime\prime\prime}&=\cos \beta \cos \gamma x + \left( \sin \alpha \sin \beta \cos \gamma -\cos \alpha \sin \gamma \right) y + \left(\cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma \right)z\\
y^{\prime\prime\prime}&=\cos \beta \sin \gamma x + \left(\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma\right) y + \left(\cos\alpha \sin \beta \sin \gamma-\sin \alpha \sin \gamma \right)z\\
z^{\prime\prime\prime}&=-\sin \beta x + \sin \alpha \cos \beta y +\cos \alpha \cos \beta z
\end{align}

と、2章同様やや複雑な式になります。

(b)行列を使う場合

\(x\)軸の周りに回転する場合の座標の変換は、前述の式を行列にして、

    \[ \begin{pmatrix} x'\\ y'\\ z'\\ \end{pmatrix} = \begin{pmatrix} 1&0&0\\ 0&\cos \alpha & -\sin \alpha\\ 0&\sin \alpha & \cos \alpha\\ \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix} \]

同様に\(y\)軸の周りに回転する場合は、

    \[ \begin{pmatrix} x^{\prime\prime}\\ y^{\prime\prime}\\ z^{\prime\prime}\\ \end{pmatrix} = \begin{pmatrix} \cos \beta &0 & \sin \beta\\ 0&1&0\\ -\sin \beta &0& \cos \beta\\ \end{pmatrix} \begin{pmatrix} x'\\ y'\\ z'\\ \end{pmatrix} \]

\(z\)軸の周りに回転する場合は、

    \[ \begin{pmatrix} x^{\prime\prime\prime}\\ y^{\prime\prime\prime}\\ z^{\prime\prime\prime}\\ \end{pmatrix} = \begin{pmatrix} \cos \gamma &-\sin \gamma &0\\ \sin \gamma & \cos \gamma & 0\\ 0 & 0 & 1\\ \end{pmatrix} \begin{pmatrix} x^{\prime\prime}\\ y^{\prime\prime}\\ z^{\prime\prime}\\ \end{pmatrix} \]

となります。

以上より設問の答えは、

    \[ \begin{pmatrix} x^{\prime\prime\prime}\\ y^{\prime\prime\prime}\\ z^{\prime\prime\prime}\\ \end{pmatrix} = \begin{pmatrix} \cos \gamma &-\sin \gamma &0\\ \sin \gamma & \cos \gamma & 0\\ 0 & 0 & 1\\ \end{pmatrix} \begin{pmatrix} \cos \beta &0 & \sin \beta\\ 0&1&0\\ -\sin \beta &0& \cos \beta\\ \end{pmatrix} \begin{pmatrix} 1&0&0\\ 0&\cos \alpha & -\sin \alpha\\ 0&\sin \alpha & \cos \alpha\\ \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ \end{pmatrix} \]

です。

回転行列により、より直観的に回転が表されると思います。

ここでは述べませんが、平行移動や拡大などを組み合わせることも容易にできます。

また、回転前の座標値を\(X\)、回転後の座標値を\(X^{\prime\prime\prime}\)、回転行列をそれぞれ\(R_x\left(\alpha\right)\)、\(R_y\left(\beta\right)\)、\(R_z\left(\gamma\right)\)とすると、

$$X^{\prime\prime\prime}=R_z\left(\gamma\right)R_y\left(\beta\right)R_x\left(\alpha\right)X$$

と、文字で表すことができます。

※回転行列の詳細は別のページで説明する予定です。

4 まとめ

最も大きな利点は、複数の数をまとめて表すことにより表現が簡潔になるということだと思います。

また、行列に共通する有用な性質があり、それらを利用することにより演算の量が減ったり問題の見通しが良くなる場合があります。本ページではあまりそのような例を示すことができませんでしたが、例えば問1.4のように、行列を使って連立\(1\)次方程式を解くことができます。