「マクスウェルの方程式1-4」で\(\boldsymbol{E}\)や\(\boldsymbol{B}\)などを使った式について述べてきましたが、電磁ポテンシャルを使うことにより計算が簡単になる場合があります。本ページではこの導出について簡単に述べます。
1 電磁ポテンシャルによる置き換え
1.1 \(\boldsymbol{E}\)、\(\boldsymbol{B}\)によるマクスウェルの方程式
以下は\(\boldsymbol{E}\)、\(\boldsymbol{B}\)によるマクスウェル方程式(微分形式)です。この後で参照します。
ガウスの法則
$$\nabla \cdot \boldsymbol{E} = \frac {\rho} {\epsilon_0} \tag{1}$$
磁場に関するガウスの法則
$$ \nabla \cdot \boldsymbol{B} = 0 \tag{2}$$
マクスウェル – ファラデーの式
$$ \nabla \times \boldsymbol{E} = – \frac {\partial \boldsymbol {B}} {\partial t} \tag{3}$$
アンペール – マクスウェルの式
$$ \nabla \times \boldsymbol{B} = \mu_0 \left( \boldsymbol {J} + \epsilon_0 \frac {\partial \boldsymbol {E} } { \partial t} \right) \tag{4}$$
1.2 ベクトル解析に関する公式
任意のベクトル\(\boldsymbol{F}\)、スカラー\(g\)に対し以下の関係が成り立ちます。これらも後で使用します。
$$\nabla \cdot \left(\nabla \times \boldsymbol {F}\right)=0 \tag{5}$$
$$\nabla \times \left(\nabla {g}\right) = \boldsymbol{0} \tag{6}$$
$$\nabla \times \left(\nabla \times \boldsymbol{F}\right)=\nabla\left(\nabla \cdot \boldsymbol{F}\right) – \nabla^2 \boldsymbol{F} \tag{7}$$
\( \nabla^2\)は以下の意味です。
$$\frac {\partial ^2}{\partial x^2} + \frac {\partial ^2}{\partial y^2} + \frac {\partial ^2}{\partial z^2}$$
これをラプラス演算子(ラプラシアン)とよびます。\(\Delta\)で表すこともあります。
1.3 磁場に関するガウスの法則\( (2) \)の置き換え
\( (5) \)と\( (2) \)を比べてください。
$$ \nabla \cdot \boldsymbol{B} = 0 \tag{2}$$
$$\nabla \cdot \left( \nabla \times \boldsymbol {F} \right) = 0 \tag{5}$$
右辺は同じであり、左辺はどちらも発散\(\nabla \cdot\)を求めています。
したがって以下のようなベクトルを定義することが可能です。
$$\boldsymbol {B}=\nabla \times \boldsymbol{A} \tag{8}$$
この\(\boldsymbol{A}\)をベクトルポテンシャルとよびます。
しかし、このように定義することに疑問を感じなかったでしょうか。
実は\( (8) \)は必ず\( (2) \)の関係を満たしますが、\( (2) \)を満たすのは\( (8) \)だけではありません。このことについては後述します。
1.4 マクスウェル – ファラデーの式\( (3) \)の置き換え
前節で定義した
$$\boldsymbol {B}=\nabla \times \boldsymbol{A} \tag{8}$$
を、マクスウェル – ファラデーの式
$$ \nabla \times \boldsymbol{E} = – \frac {\partial \boldsymbol {B}} {\partial t} \tag{3}$$
に代入すると、
$$ \nabla \times \boldsymbol{E} = – \frac {\partial} {\partial t} \left(\nabla \times \boldsymbol{A} \right)$$
右辺の空間微分\(\nabla \times \)と時間微分\( \displaystyle \frac {\partial } {\partial t}\)を入れ替えて、
$$ \nabla \times \boldsymbol{E} = – \nabla \times \frac {\partial \boldsymbol{A}} {\partial t}$$
$$ \nabla \times \left( \boldsymbol{E} + \frac {\partial \boldsymbol{A}} {\partial t} \right) =\boldsymbol{0}$$
これをベクトル解析の公式
$$\nabla \times \nabla {g} = \boldsymbol{0} \tag{6}$$
と比較すると、右辺の括弧の中はスカラーの勾配で表されることがわかります。
そこでスカラーを\(-\Phi\)とし、
$$\boldsymbol{E} + \frac {\partial \boldsymbol{A}} {\partial t}=-\nabla \Phi$$
移項して
$$\boldsymbol{E} = -\frac {\partial \boldsymbol{A}} {\partial t} -\nabla \Phi\tag{9}$$
と定義します。
スカラーに負号をつけた理由については3.1節で述べます。
この\(\Phi\)を静電ポテンシャルとよびます。また、ベクトルポテンシャルと静電ポテンシャルを合わせて電磁ポテンシャルとよびます。
1.5 ガウスの法則\( (1) \)の置き換え
前節で定義した\( (9) \)をガウスの法則
$$\nabla \cdot \boldsymbol{E} = \frac {\rho} {\epsilon_0} \tag{1}$$
に代入します。
$$- \nabla \cdot \left( \nabla \Phi + \nabla \cdot \frac {\partial \boldsymbol{A}} {\partial t} \right) = \frac {\rho} {\epsilon_0} $$
さらに上の式の2項目は空間微分と時間微分を入れ替えて、
$$- \nabla^2 \Phi – \frac {\partial} {\partial t}\nabla \cdot \boldsymbol{A} = \frac {\rho} {\epsilon_0} \tag{10}$$
となります。
1.6 アンペール – マクスウェルの式\( (4) \)の置き換え
同様に\( (5) \)と\( (9) \)をアンペール – マクスウェルの式
$$ \nabla \times \boldsymbol{B} = \mu_0 \left( \boldsymbol {J} + \epsilon_0 \frac {\partial \boldsymbol {E} } { \partial t} \right) \tag{4}$$
に代入します。
$$ \nabla \times \nabla \times \boldsymbol{A} = \mu_0 \left\{ \boldsymbol {J} – \epsilon_0 \frac {\partial } { \partial t} \left( \frac {\partial \boldsymbol{A}} {\partial t} + \nabla \Phi \right) \right\}$$
左辺にベクトル解析の公式
$$\nabla \times \left(\nabla \times \boldsymbol{F}\right)=\nabla\left(\nabla \cdot \boldsymbol{F}\right) – \nabla^2 \boldsymbol{F} \tag{7}$$
を適用し、
$$ \nabla\left(\nabla \cdot \boldsymbol{A}\right) – \nabla^2 \boldsymbol{A} = \mu_0 \boldsymbol {J} – \epsilon_0 \mu_0 \frac {\partial^2 \boldsymbol{A}} {\partial t^2} + \epsilon_0 \mu_0 \nabla \frac {\partial \Phi}{\partial t} $$
さらに
$$\epsilon_0 \mu_0 = \frac {1} {c^2}$$
を代入し整理すると
$$\nabla \left( \nabla \cdot \boldsymbol{A} + \frac {1}{c^2} \frac{\partial \Phi} {\partial t} \right) – \left( \nabla^2 – \frac{1}{c^2}\frac{\partial^2}{\partial t^2} \right) \boldsymbol{A} = \mu_0 \boldsymbol{J} \tag{11}$$
となります。
マクスウェルの方程式を電磁ポテンシャルで表すと\( (10) \)と\( (11) \)のようになります。
やや複雑な形ですが、次章のゲージ変換によりさらに式を変形することができます。
2 ゲージ変換
2.1 ベクトルポテンシャルの自由度
前章では磁場に関するガウスの法則\( (2) \)とマクスウェル – ファラデーの式\( (3) \)よりベクトルポテンシャルと静電ポテンシャルを定義しました。
しかしこれらの条件からは電磁ポテンシャルは一意に決まるわけではありません。
つまり前章の定義は間違いではありませんが他にも条件を満たす電磁ポテンシャルがあります。これらについて考えましょう。
磁場に関するガウスの法則は以下でした。
$$ \nabla \cdot \boldsymbol{B} = 0 \tag{2}$$
ベクトルポテンシャルに添え字をつけます。
$$\boldsymbol {B}=\nabla \times \boldsymbol{A}_0 \tag{8-2}$$
ここで、ベクトル解析の公式
$$\nabla \times \nabla {g} = \boldsymbol{0} \tag{6}$$
を使います。右辺は\(\boldsymbol{0}\)なので式\( (8-2) \)の両辺に\( (6) \)の左辺を追加しても等号は成立することがわかります。\(g\)を\(\chi\)に変え、
$$\boldsymbol {B}=\nabla \times \boldsymbol{A}_0 + \nabla \times \left( \nabla \chi \right) $$
右辺をまとめ
$$\boldsymbol {B}=\nabla \times \left( \boldsymbol{A}_0 + \nabla \chi \right) $$
したがって
$$\boldsymbol{A} = \boldsymbol{A}_0 + \nabla \chi \tag{12}$$
としても
$$\boldsymbol{B}= \nabla \times \boldsymbol{A} $$
の定義を変える必要はありません。つまり\(\nabla \chi\)だけの自由度があります。
2.2 静電ポテンシャルの自由度
前節の\(\chi\)によって静電ポテンシャルがどのように表されるかを考えます。
以下の定義(\(\Phi\)は添え字を追加しています)に
$$\boldsymbol{E} = -\frac {\partial \boldsymbol{A}} {\partial t} -\nabla \Phi_0\tag{9-2}$$
\( (12) \)を代入します。
$$\boldsymbol{E} = -\frac {\partial } {\partial t}\left(\boldsymbol{A}_0 + \nabla \chi\right) -\nabla \Phi_0$$
入れ替えて、
$$\boldsymbol{E} = -\nabla \left( \Phi_0 + \frac{\partial \chi} {\partial t} \right) -\frac {\partial \boldsymbol{A}_0} {\partial t} $$
したがって、
$$\Phi=\Phi_0+\frac{\partial \chi} {\partial t} \tag{13}$$
としても電磁ポテンシャルの定義を変える必要はありません。つまり\(\displaystyle \frac{\partial \chi} {\partial t} \)だけの自由度があります。
2.3 ゲージ変換
2.1節、2.2節で導いたように、前章で定義した電磁ポテンシャルには自由度があります。したがって、ある決められた電磁ポテンシャルより、別の電磁ポテンシャルに変換することができます(変換しても前章のマクスウェルの方程式\( (10) \)、\( (11) \)が成立します)。
この変換をゲージ変換とよびます。ゲージ変換は以下の式です。ややこしい書き方ですが、2.1節、2.2節で求めた式を変換として表しただけです。
$$\boldsymbol{A} \mapsto \boldsymbol{A}’ = \boldsymbol{A} + \nabla \chi \tag{14}$$
$$\Phi \mapsto \Phi ^{\prime} =\Phi+\frac{\partial \chi} {\partial t} \tag{15}$$
2.4 ローレンツゲージ
ここまで述べてきたように\( (8) \)と\( (9) \)の定義だけでは電磁ポテンシャルは一意に決まりません。しかし、計算しやすいよう条件を追加することもできます。その条件も一種類ではありませんが、よく使われるものに下記のローレンツゲージがあります。
$$\nabla \cdot \boldsymbol{A}+\frac{1}{c^2} \frac{\partial \Phi}{\partial t}=0\tag{16}$$
ローレンツゲージをマクスウェルの方程式に適用してみましょう。
改めて、マクスウェルの方程式です。
$$- \nabla^2 \Phi – \frac {\partial} {\partial t}\nabla \cdot \boldsymbol{A} = \frac {\rho} {\epsilon_0} \tag{10}$$
$$\nabla \left( \nabla \cdot \boldsymbol{A} + \frac {1}{c^2} \frac{\partial \Phi} {\partial t} \right) – \left( \nabla^2 – \frac{1}{c^2}\frac{\partial^2}{\partial t^2} \right) \boldsymbol{A} = \mu_0 \boldsymbol{J} \tag{11}$$
\( (16) \)より\( (10) \)の\(\nabla \cdot \boldsymbol{A}\)を消去し符号を反転すると、
$$ \left( \nabla^2 – \frac{1}{c^2} \frac {\partial^2} {\partial t^2} \right) \Phi = -\frac {\rho} {\epsilon_0} \tag{17}$$
\( (16) \)より\( (11) \)左辺の前半を消去し符号を反転すると、
$$ \left( \nabla^2 – \frac{1}{c^2} \frac {\partial^2} {\partial t^2} \right) \boldsymbol{A} = -\mu_0 \boldsymbol{J} \tag{18}$$
と、対称的で簡潔な形になりました。
式の中の
$$ \nabla^2 – \frac{1}{c^2} \frac {\partial^2} {\partial t^2}$$
はダランベール演算子(ダランベルシアン)とよばれ\( □\)で表されます。これを用いると、
$$ □ \Phi = -\frac {\rho} {\epsilon_0} \tag{19}$$
$$ □ \boldsymbol{A} = -\mu_0 \boldsymbol{J} \tag{20}$$
と、さらに簡潔になります。
2.5 4元ベクトル
\( (19) \)の両辺はスカラー、\( (20) \)の両辺は3次元のベクトルです。これらを一つにまとめた4次元の電磁ポテンシャルと電流密度ベクトルを定義します。
電磁ポテンシャルは、
$$A^{\nu}=\left(\frac{\Phi}{c} ,\boldsymbol{A}\right)$$
電流密度は、
$$J^{\nu}=\left(c \rho, \boldsymbol{J} \right)$$
とします。
\(\nu\)は\(0\)から\(3\)の整数で、\(A^0 \cdots A^3\)はそれぞれの成分を示します。\(J^0 \cdots J^3\)も同様です。
\( (19) \)の両辺を\(c\)で割ると
$$ □ \frac{\Phi}{c} = -\frac {\rho} {c\epsilon_0}$$
右辺の分母と分子に\(c\mu_0\)を掛けると、
$$ □ \frac{\Phi}{c} = -\frac {c \mu_0\rho} {c^2 \epsilon_0 \mu_0}$$
\(c\)と\(\epsilon_0\)、\(\mu_0\)は、
$$c^2=\frac{1}{\epsilon_0\mu_0}$$
の関係にあるので、
$$ □ \frac{\Phi}{c} = -c \mu_0\rho$$
したがって\( (19) \)と\( (20) \)は、
$$ □ A^{\nu} = -\mu_0 J^{\nu} \tag{21}$$
と表すことができます。
4つの式で構成されたマクスウェルの方程式は1つにまとめることができました。
このようにベクトルを定義するのは単に式をまとめるためというわけではなく、相対性理論で用いられる4元ベクトルと同じ考え方であるからだと思います。
\( (21) \)が相対性理論における4元ベクトルと関連してどのような意味をもつかについてはいずれ相対性理論のページで述べたいと思います。
3 その他
3.1 静電ポテンシャルの定義に負号がつく理由
電場、ベクトルポテンシャル、静電ポテンシャルの関係は以下でしたが、
$$\boldsymbol{E} = -\frac {\partial \boldsymbol{A}} {\partial t} -\nabla \Phi\tag{9}$$
以下のようにすることもできたはずです。
$$\boldsymbol{E} = -\frac {\partial \boldsymbol{A}} {\partial t} +\nabla \Phi$$
しかし、このように符合を決めたのは電位を静電ポテンシャルとみなすためでしょう。静電磁場であるとすれば\( (9) \)における電場と静電ポテンシャルは以下の関係になります。
$$\boldsymbol{E} = -\nabla \Phi$$
これは電場と電位の関係そのものです(「マクスウェルの方程式3」3.2節)。
つまり\( (9) \)のように定義することにより、\( \Phi\)は電位と考えることができます。
なお、電場と電位の符号について補足します。
次の図のように電極が2枚あり片側は正の電荷、もう片側は負の電荷が帯電しているとします。
両者の間には電場が生じますが、その向きは正から負です。

電場が生じることにより電位差も生じますが、その電位は負側が低く、正側が高くなります。
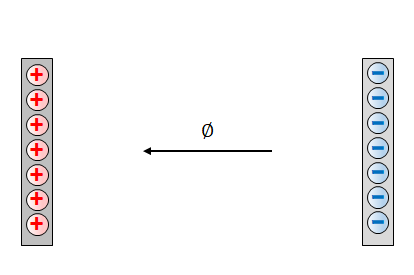
負号がつくのはこの定義の違いによるものです。
4 まとめ
・以下を電磁ポテンシャルとよびます。
$$\boldsymbol {B}=\nabla \times \boldsymbol{A}$$
$$\boldsymbol{E} = -\frac {\partial \boldsymbol{A}} {\partial t} -\nabla \Phi$$
・電磁ポテンシャルによりマクスウェルの方程式は以下のように表されます。
$$- \nabla^2 \Phi – \frac {\partial} {\partial t}\nabla \cdot \boldsymbol{A} = \frac {\rho} {\epsilon_0} $$
$$\nabla \left( \nabla \cdot \boldsymbol{A} + \frac {1}{c^2} \frac{\partial \Phi} {\partial t} \right) – \left( \nabla^2 – \frac{1}{c^2}\frac{\partial^2}{\partial t^2} \right) \boldsymbol{A} = \mu_0 \boldsymbol{J} $$
・条件を追加することにより電磁ポテンシャルを一意に決めることができます。その一つであるローレンツゲージは以下で表されます。
$$\nabla \cdot \boldsymbol{A}+\frac{1}{c^2} \frac{\partial \Phi}{\partial t}=0$$
ローレンツゲージによりマスクスウェルの方程式は以下に変わります。
$$ □ \Phi = -\frac {\rho} {\epsilon_0}$$
$$ □ \boldsymbol{A} = -\mu_0 \boldsymbol{J}$$
・さらに4元ベクトルにより
$$ □ A^{\nu} = -\mu_0 J^{\nu} $$
と表されます。
