特殊相対性理論ではミンコフスキー図がよく使われます。これは時間と空間を同一平面で表したものです。一般的には時空図といいますが、特殊相対性理論に対応した図を特にミンコフスキー図とよびます。本ページではこの図について説明します。
1.1 ミンコフスキー図とは
ミンコフスキー図では1つの座標軸を時間にします。ただし\(t\)ではなく\(c\)をかけて\(ct\)として表します\(ct\)は距離を表すので空間と同じ次元です。
我々がイメージできるのは3次元までなので、空間は2次元または1次元しか表すことができません。ここでは\(x\)のみを表すことにします。
縦軸は\(ct\)、横軸は\(x\)です。見慣れない図ですが、高校の物理で、縦軸を距離、横軸を時間としたグラフを目にしたことと思います。このグラフの縦と横を入れ替えた図です。

上の図は\(S\)の座標軸のみですが、これに\(S’\)の座標軸を追加します。
軸を決めるために、次節でローレンツ変換について補足します。
1.2 ローレンツ変換
ローレンツ変換は以下でした。
$$t’=\gamma \left(t-\frac{vx}{c^2} \right) \tag{1}$$
$$x’=\gamma (x-vt)\tag{2}$$
$$y’=y\tag{3}$$
$$z’=z\tag{4}$$
これを少し変形します。
\( (3) \)と\( (4) \)は使いません。
\( (1) \)の両辺に\(c\)を掛けると
$$ct’=\gamma \left(ct-\frac{vx}{c} \right) \tag{5}$$
ローレンツ因子\(\displaystyle \beta=\frac {v} {c} \)を代入すると\( (5) \)、\( (2) \)は
$$ct’=\gamma ct- \beta \gamma x \tag{6}$$
$$x’=\gamma x – \beta \gamma ct\tag{7}$$
となります。本ページでは\( (6) \)、\( (7) \)をローレンツ変換として使います。
次に逆変換を求めます。過程は省略しますが左辺に\(ct\)と\(x\)を移動させると、
$$ct=\gamma ct’ + \beta x’ \tag{8}$$
$$x=\gamma x’ + \beta \gamma ct’\tag{9}$$
という、それぞれ2項目の符号が反転するだけで係数が同じ式になります。
1.3 \(ct’\)軸
ミンコフスキー図上で\(ct’\)の軸をどう描くかを考えます。
\(ct’\)軸上では\(x’\)は\(0\)、\(ct’\)は任意の値です。したがって、このときの\(ct\)、\(x\)を求め、図にプロットすれば\(ct’\)軸になります。
\(ct\)と\(x\)は\( (8) \)と\( (9) \)から求めれるのでこれらに\(x’=0\)を代入すると、
$$ct=\gamma ct’$$
$$x=\beta \gamma ct’$$
2番目の式の\(\beta\)を移動し、
$$\frac{x}{\beta}=\gamma ct’$$
\(\gamma ct’\)を消去し、
$$ct=\frac{1}{\beta}x \tag{10}$$
したがって\(ct’\)軸は図のように傾き\(\displaystyle \frac {1}{\beta}\)の線になります 。
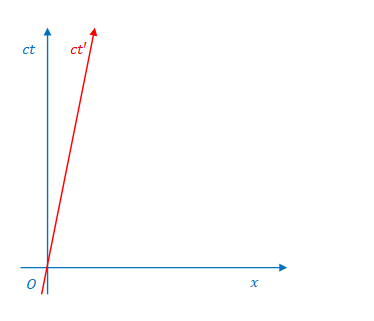
\(ct\)軸と\(ct’\)軸は一致しません。\(S\)から見ると\(S’\)は移動しているからです。
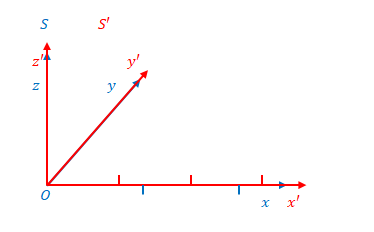
次に示す2つの図の上のほうは、\(x\)、\(y\)、\(z\)の直交座標系(ここでは3次元空間とよぶことにします)です。\(y\)と\(z\)はミンコフスキー図に関係ありませんが見やすくするよう3次元で描いています。下のほうがミンコフスキー図です。
ミンコフスキー図における\(ct\)軸と\(ct’\)軸の\(x\)方向の距離は3次元空間における\(S\)と\(S’\)の原点の距離と考えることができます。
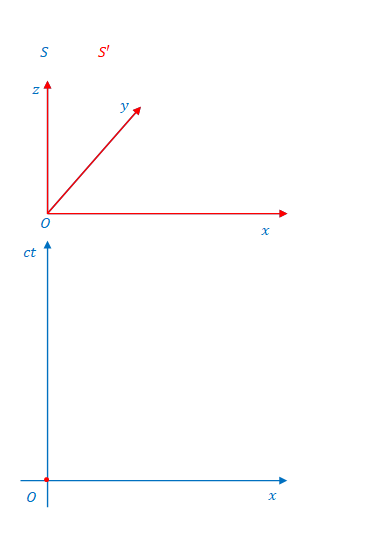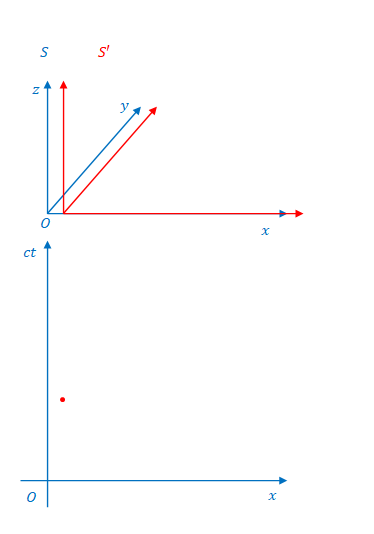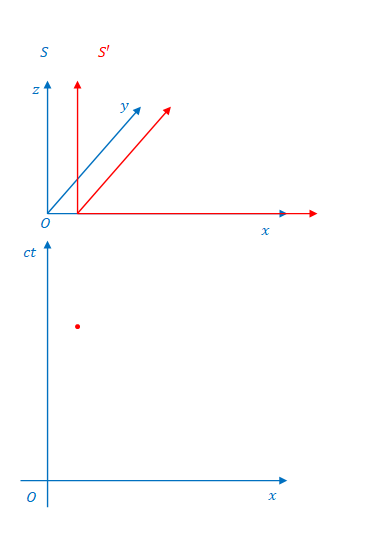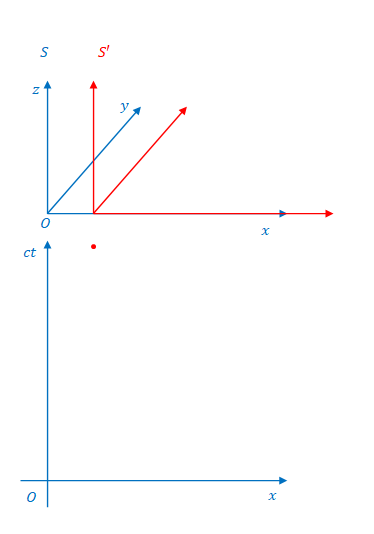
1.4 \(x’\)軸
同様に\( x’\)を変数、\( ct’\)を\(0\)の定数としたときの\(ct\)、\(x\)を図にプロットすれば\(x’\)軸になります。
\( (8) \)、\( (9) \)に\(ct’=0\)を代入し、
$$ct=\beta \gamma x’ $$
$$x=\gamma x’$$
\(\gamma x’\)を消去し、
$$ct = \beta x\tag{11}$$
したがって\(x’\)軸は傾き\(\beta\)の線になります。
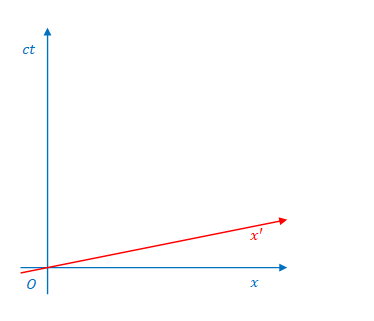
なぜ\(x’\)軸は\(x\)軸と同じ方向にならないのでしょう。\(ct’\)軸の場合と同様、ローレンツ逆変換から導くことは簡単です(上述の通りです)。具体的に思い描くのは簡単ではないのですが、ミンコフスキー図の性質を知るために考えてみましょう。
\(ct=0\)の瞬間のみ、原点(\(A\)とします)と、\(x’>0\)のある点(\(B\)とします)でライトが点灯したとします。
この瞬間、\(ct’\)はどれだけになるでしょう。
2通りに分けて考えます。
(a)\(S’\)の座標を\(S’\)で静止している観測者が見た場合
まず、\(S’\)の座標を、\(S’\)で静止している観測者から見た場合について考えてみましょう、\(S’\)の座標を観測しているのが\(S’\)で静止している観測者ではない点に注意してください。
\(S\)の座標は\(S\)で静止している観測者から観測することにします。
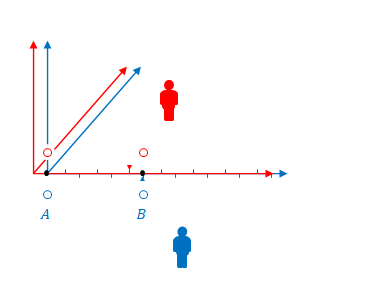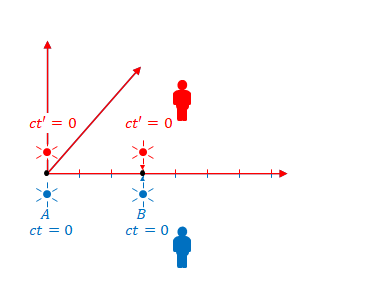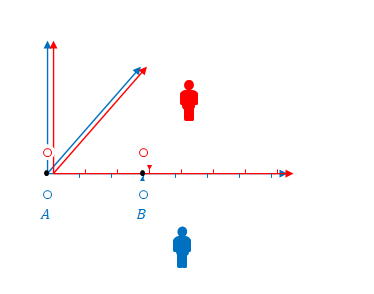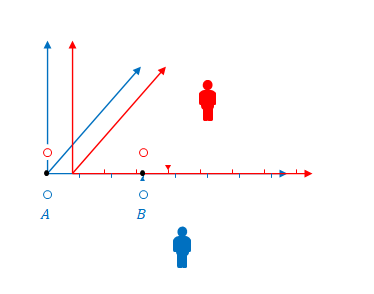
下の図で、\(S\)と\(S’\)の原点が重なる瞬間に注目してください。
この時、\(S\)から見ると、\(A\)は\((ct,x)=(0,0)\)、\(B\)は\((ct,x)=(0,3)\)(\(x\)座標の\(1\)目盛を\(1\)とします)です。
\(S’\)の座標系ではどうでしょう。この場合\(S\)ではなく\(S’\)が観測しているので、目盛の広さは\(S\)と同じです。時間の遅れもローレンツ収縮もありません。
\(S\)から見て\(A\)が\((ct,x)=(0,0)\)、\(B\)が\((ct,x)=(0,3)\)で点灯するのであれば\(S’\)から見ても\(A\)が\((ct’,x’)=(0,0)\)、\(B\)が\((ct’,x’)=(0,3)\)で点灯するはずです。
(b)\(S’\)の座標を\(S\)で静止している観測者が見た場合
今求めたいのは、\(S’\)の座標を\(S’\)で静止している観測者から見た場合ではなく、\(S\)で静止している観測者から見た場合です。 観測者を変えて考えましょう。
\(S\)から見ても\(A\)が\((ct’,x’)=(0,0)\)、\(B\)が\((ct’,x’)=(0,3)\)で点灯することに変わりはありません。しかし\(S\)から\(S’\)を見ると時間は遅れるし空間は収縮します。
では(a)の場合と何が異なるのでしょう。
下の図の原点(\(A\)の位置)が一致した瞬間を確認してください。原点なのでこの時\(ct’=0\)です。したがって点灯します。
しかし、この瞬間、\(B\)の\(x’\)座標と\(x\)座標は一致しません。図の三角の目印に注目してください。それぞれの座標における\(3\)の位置です。\(B\)では\(x=3\)に対し\(x’>3\)です。
\(S\)から見て\(S’\)は右に移動しているので、いずれ\(B\)の\(x’\)座標と\(x\)座標が一致する瞬間がきます(三角の位置が一致する時です)。その瞬間こそが\(B\)における\(ct’=0\)です。
しかし原点が一致している瞬間はそれより遡らないといけないので、その時点では\(B\)では\(ct'<0\)のはずです。
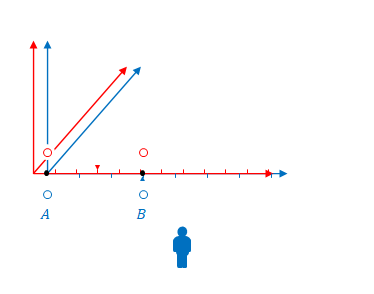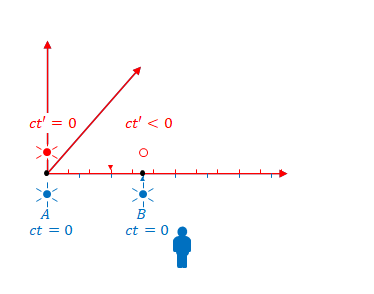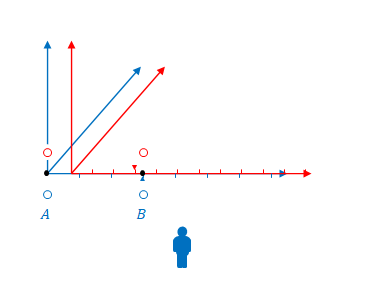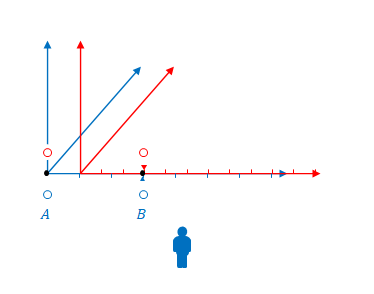
以上より、\(S\)から見ると\(S\)の時間(\(ct\))は位置によって当然変わらないのですが、\(S’\)の時間(\(ct’\))は位置によって変わることがわかります。
逆の見方をすれば、\(ct’\)がある値となる\(ct\)は位置によって異なるともいえます。そして\(ct’=0\)となるのは\(x\)と\(x’\)が一致した位置、時刻(\(ct\))です。
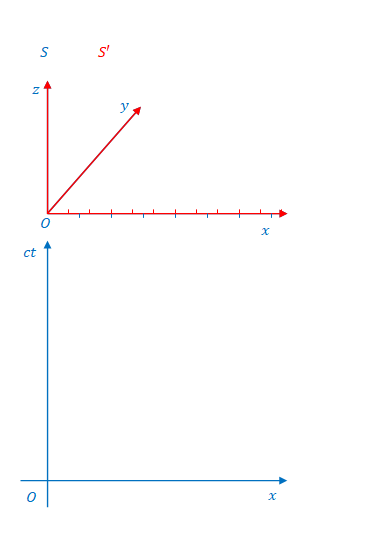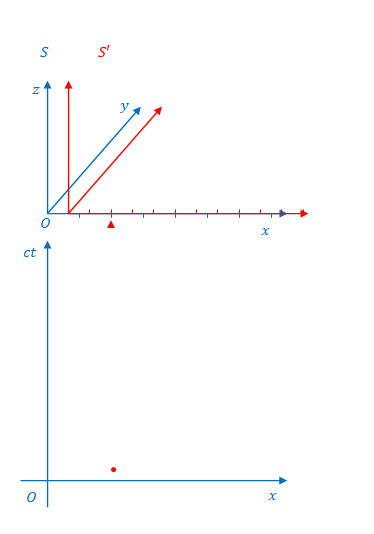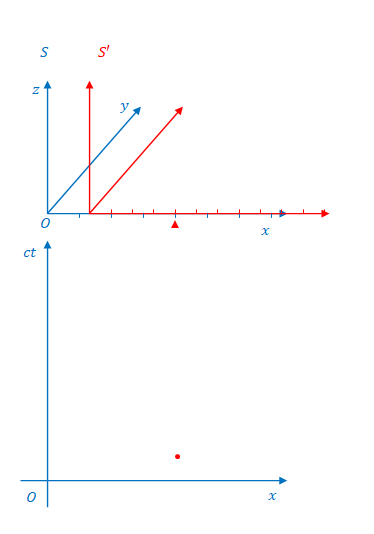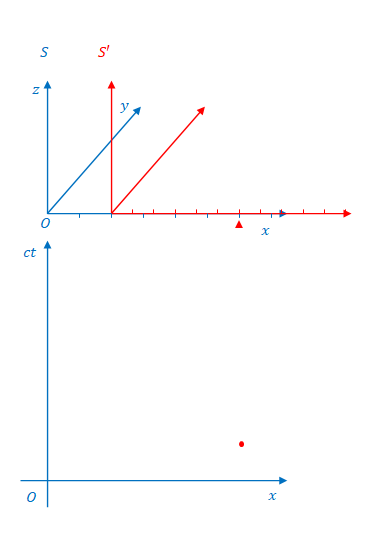
下の図はミンコフスキー図の点と3次元空間の図の三角は\(x=x’\)となったところを描画しています。図では離散的ですが、実際にはこれが連続して発生しています。その点を結んだものが\(x’\)軸です。
1.5 ミンコフスキー図の見方
ミンコフスキー図上の点と座標の値との関係を確認しましょう。
ここまでの図の通り、通常、\(S\)座標の軸は垂直に交わるようにします。\(S’\)座標の軸は\(S\)座標とは向きが異なります。
次に\(S’\)座標についてです。\(ct’\)軸は傾きがあることがわかりました。\(x’=0\)となる点を結ぶと\(ct\)の増加につれて\(x\)が増加するからでした。同様に\(x’\)が任意の値の場合の線は\(ct’\)軸に平行になることは容易にわかります。
また、\(ct’\)が任意の場合も\(x’\)軸に平行線になります。
参考ですが、\(ct\)、\(x\)の目盛線を引くと長方形の格子に、\(ct’\)と\(x’\)の目盛線を引くと平行四辺形になります。

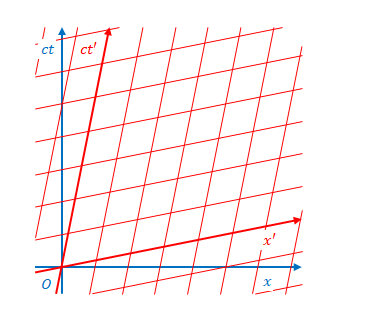
つまり、ある点の\(S\)、\(S’\)上での座標は、その点を通る、軸に平行な線を引き、もう一方の軸と交わるところを求めればよいことがわかります。
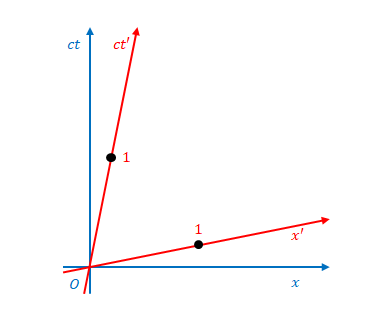
例えば図の点が\((ct,x)=(1,1)\)であったとします。

\(ct’\)軸、\(x’\)軸と平行な線を引くと\((ct’,x’)\)を読み取ることができます。

これらの値は、\( (6) \)、\( (7) \)に\(ct=1\)、\(x=1\)を代入することにより\((ct’,x’)=(\gamma-\beta\gamma, \gamma-\beta\gamma)\)であるとわかります。
逆に、\((ct’,x’)=(1,1)\)の点から
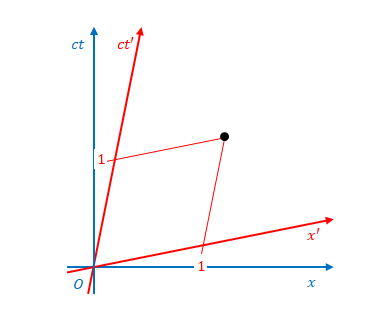
\(ct\)軸、\(x\)軸に平行な線を引くと\((ct,x)\)が求められます。
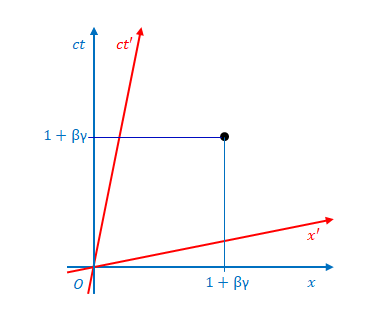
これらの値は、\( (8) \)、\( (9) \)に\(ct’=1\)、\(x’=1\)を代入することにより\((ct,x)=(\gamma+\beta\gamma, \gamma+\beta\gamma)\)であることがわかります。
1.6 目盛の広さの違い
\(S\)と\(S’\)では目盛りの広さ(間隔)はどれだけ変わるでしょう。
\((ct,x)=(1,0)\)、\((ct,x)=(0,1)\)をローレンツ変換すると、
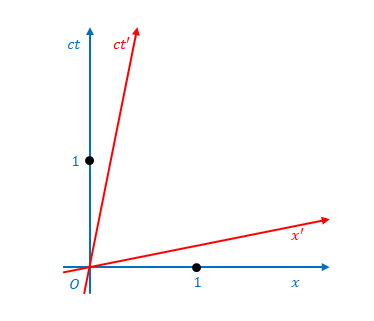
それぞれ\((ct’,x’)=(\gamma,-\beta \gamma)\)、\((ct’,x’)=(-\beta \gamma,\gamma)\)になります。
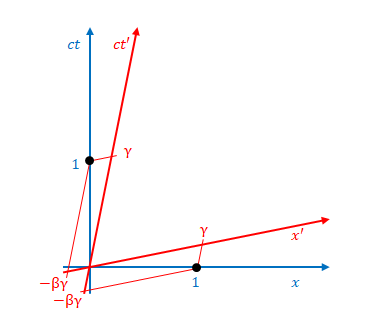
\((ct’,x’)=(1,0)\)、\((ct’,x’)=(0,1)\)をローレンツ逆変換すると、
\((ct,x)=(\gamma,\beta \gamma)\)、\((ct,x)=(\beta \gamma,\gamma)\)になります。

結局どちらの目盛が広いのでしょうか。
最後の図の\((ct,x)=(\beta \gamma,\gamma)\)の原点からの長さは、
$$\sqrt {\gamma^2+\beta^2 \gamma^2} =\sqrt {(1+\beta^2)\gamma^2} = \sqrt {\frac{1+\beta^2}{1-\beta^2} } $$
です。
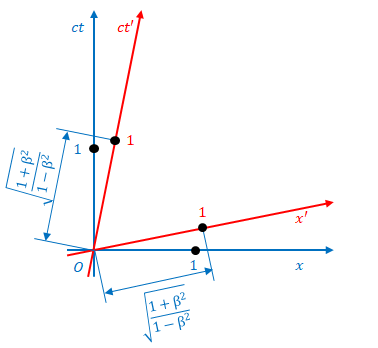
この点が\(S’\)では\((ct’,x’)=(0,1)\)なので原点からの長さは\(1\)です。
つまり、ミンコフスキー図上では\(x’\)の目盛の広さは\(x\)の目盛の広さの\(\displaystyle \sqrt {\frac{1+\beta^2}{1-\beta^2} } \)倍です。
\(ct’\)と\(ct\)の目盛の広さの関係も同じです。
\(\displaystyle \sqrt {\frac{1+\beta^2}{1-\beta^2} } \)は明らかに\(1\)より大きいので目盛も\(S\)より\(S’\)のほうが広いということになります。
3次元空間では\(x’\)軸の目盛の広さは\(x\)軸の\(\displaystyle\frac{1}{\gamma}\)倍になります。ミンコフスキー図とは広さの関係が異なる点に注意してください。
違いを理解するのは難しいのですが、3次元空間において観測される目盛の広さ、つまり長さとは\(ct\)が固定の状態で決まるものであるのに対し、ミンコフスキー図における\(x’\)軸の目盛の広さとは\(ct’\)が固定の状態で決まるもの、と考えてください。
1.7 \(v\)による\(ct’\)、\(x’\)の変化
\(ct’\)軸と\(x’\)軸の傾きはそれぞれ\(\displaystyle \frac{1}{\beta}\)、\(\beta\)でした。\(\displaystyle \beta=\frac{v}{c}\)なので、下の図のように傾きは\(v\)によって変化します。
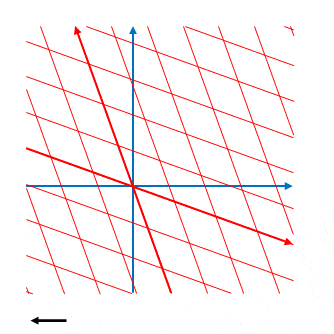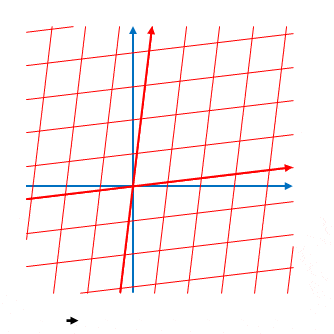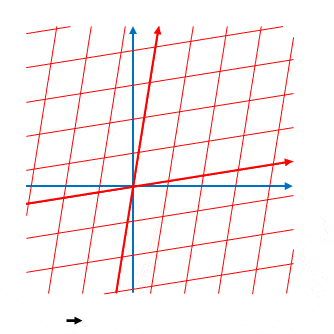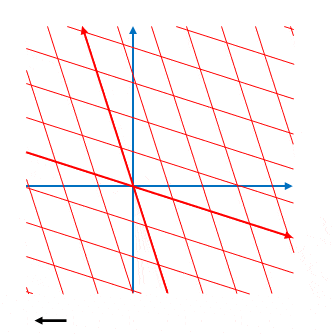
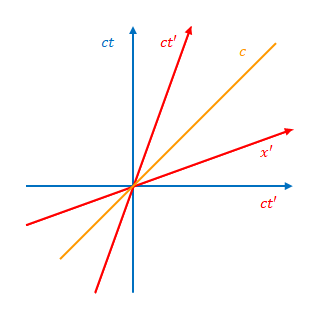
\(v\)が(正の場合)大きくなるほど\(ct’\)の軸の傾きが小さく、\(x’\)の軸の傾きは大きくなります。しかし必ず\(v \lt c\)つまり\(\beta \lt 1\)なので \(ct’\)の傾きが\(1\)以下、\(x’\)の傾きが\(1\)以上になることはありません。
この傾き\(1\)の線は光の軌跡(光の世界線)です。
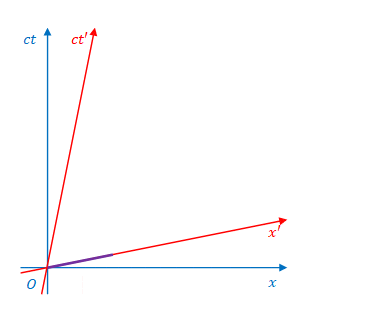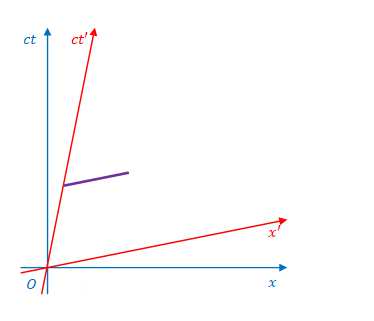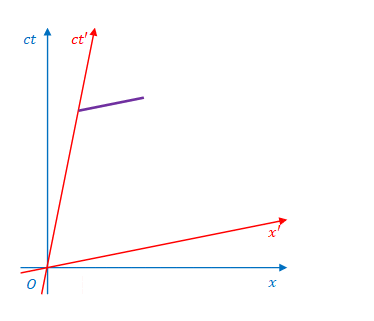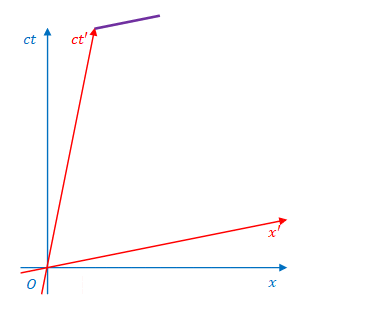
1.8 \(x\)軸または\(x’\)軸に固定された棒の時間経過
3次元座標で見た場合に\(x’\)軸上で静止している棒がミンコフスキー図上でどのように表されるかを考えてみましょう。
棒の左端が\(S’\)座標の原点にあるとすれば、ミンコフスキー図では、左端は\(ct’\)軸に沿って動きます。
棒の向きはどの時間座標に合わせて見るかにより異なります。
下の図は\(ct\)に合わせて見た場合です。それぞれの瞬間は、どの位置でも同じ\(ct\)です。したがって、ミンコフスキー図上では\(x\)軸に平行になります。

\(ct’\)に合わせて見た場合は棒は\(x’\)に平行になります。
2 まとめ
・特殊相対性理論に対応した時空図をミンコフスキー図とよびます。
・ミンコフスキー図では通常、時間(に光速を掛けた値)を縦の軸、空間(1次元または2次元)を横の軸として表します。
・\(S’\)の座標軸は\(S\)の座標軸とは一致しません。その角度は\(v\)(慣性系の相対速度)によって変わります。
・光の軌跡は傾き\(1\)の直線になります。\(ct’\)軸はこれより下向き、\(x’\)軸はこれより上向きになることはありません。
