相対性理論の教科書を見ると、「反変」(はんぺん)「共変」(きょうへん)という言葉が頻繁に出てきます。特殊相対性理論だけを理解するのであればこれらを詳しく知る必要はないと思うのですが、そうはいっても気になる言葉ではあります。そこで、ここでは概要を説明します。
※本ページではベクトルなどの添え字が上に付いたり下に付いたりします。相対性理論における一般的な記法では添え字の上下を使い分けるため、それに合わせています。とりあえずは気にしないで読み進めてください。
1 ベクトルと座標に関する定義
1.1 ベクトル
以下のようにベクトルは、基準となるベクトルとそのベクトルのスカラー倍の和で表すことができます。
$$\boldsymbol {A} = A^x \boldsymbol {e}_x + A^y \boldsymbol {e}_y $$
図にすると以下のようになります。\(A_x\)、\(A_y\)は\( \boldsymbol {e}_x\)、\( \boldsymbol {e}_y\)の大きさを1区間とした場合の各方向成分の区間の数(整数とは限りません)と考えてください。
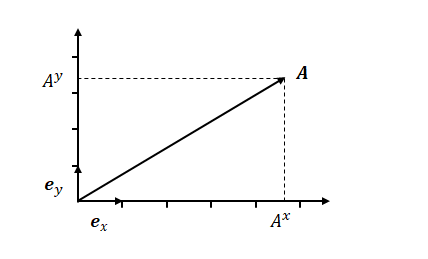
\(\boldsymbol {e}_x\)と\(\boldsymbol {e}_y\)のような、基準となるベクトルを基底ベクトル、\(A^x\)と\(A^y\)のような、倍率を表すスカラーをベクトル成分とよびます。
高校の数学で単位ベクトルという言葉を習ったかもしれません。両者は似ていますが、単位ベクトルは大きさが\(1\)、ベクトルと同じ向き、ベクトル\(1\)つにつき単位ベクトル\(1\)つであるのに対し、基底ベクトルはいずれもが必須ではありません。
例えば単位ベクトルは
$$\boldsymbol{e}=\frac{\boldsymbol{A}}{|\boldsymbol{A}|}$$
のように表されます。
基底ベクトルは以下のように定義することが可能ですが、
$$\boldsymbol {e}_x = (2,0,0) \quad \boldsymbol {e}_y = (0,2,0) \quad \boldsymbol {e}_z = (0,0,2)$$
この場合大きさは\(1\)ではなく、向きもベクトルに合わせているわけではありません。また、ベクトルと基底ベクトルの数も\(1\)対\(1\)ではありません。複数のベクトルが存在した場合でもこれらは共通の基底ベクトルとして扱うことができます。
1.2 座標に関する便宜的な定義
本ページでは座標の単位長を「座標の目盛り」とよぶことにします(一般的なよび方ではなく、ここだけの呼称です)。定規の目盛りのようなものを思い描いてください。この座標の目盛りをどうやって測るかは考えません。単にこれが広がった状態と狭まった状態を相対的に表現するためのものです。
座標の目盛りと座標の値の増減は逆になります。
以下、\(A^x\)の値に注目してください。
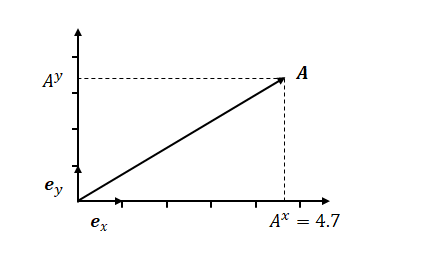
\(x\)座標の目盛りを広げたとします。
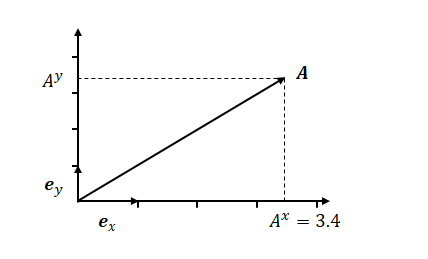
\(x\)座標の値は小さくなります。
1.3 概要
次章より共変ベクトルと反変ベクトルの定義について述べますが、その前に共変ベクトルと反変ベクトルについて以下の点、注意ください。
・以下の関係によって定義される。
-座標変換前後のベクトル成分
-座標変換前後の座標
・ただし、これらだけではイメージしづらいので本ページでは以下を合わせて考える。
-座標変換前後の基底ベクトル
-座標変換前後の座標の目盛り
・ベクトルの大きさや向きがどう変わるかで決まるものではない。
・座標変換によってどう変わるかによって決まるものであって、単一の座標上の変化だけで決まるものではない。
2 1次元の場合
2.1 反変ベクトル
下の図のように座標系\(S\)において\(x\)方向を向くベクトル\(\boldsymbol{A}\)があるとします。
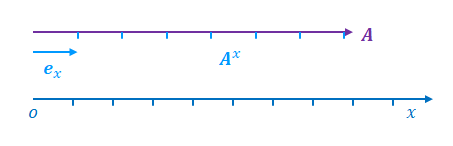
基底ベクトルを\(\boldsymbol{e}_x\)、ベクトル成分を\(A^x\)とします。図の都合上、\(\boldsymbol{e}_x\)は\(\boldsymbol{A}\)より離して描いています。
ベクトルは単位ベクトルの大きさで区切っています。ベクトル成分は区切られた区間の数(整数とは限りません)です。
\(x\)軸は座標の目盛りで区切っています。
これらが座標系\(S’\)でどう表されるかを考えます。
\(x’\)の軸と基底ベクトル\(\boldsymbol{e}’_x\)を追加します。\(x’\)は\(t=0\)の瞬間におけるローレンツ変換のようなものだと考えてください。つまり\(x’=\gamma x\)のような比例の関係にあります。
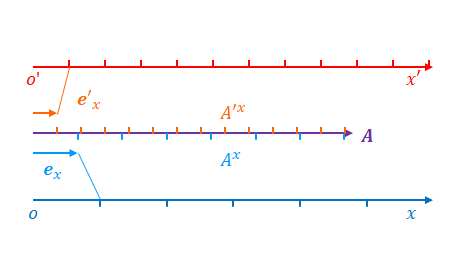
座標変換の条件が変わることにより\(x\)と\(x’\)の関係が変わったとします。ローレンツ変換の例であれば\(\gamma\)が変わる、つまり\(v\)が変わった状態です。下の図は\(x\)の目盛りを変えずに\(x’\)の目盛りが広まった状態です。
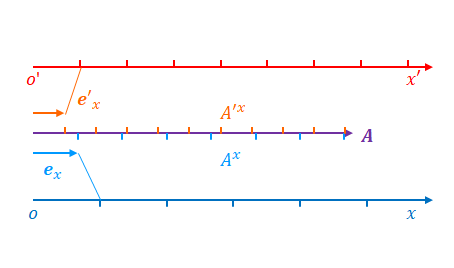
ここで基底ベクトルがどう変わるかに注目してください。反変ベクトルと共変ベクトルでは変わり方が異なります。
反変ベクトルの場合、\(x’\)の目盛りが広がると、\(\boldsymbol{e}’_x\)は大きくなります。\(\boldsymbol{e}’_x\)が大きくなると\(A’_x\)が小さくなります。
また、\(x’\)の目盛りが広がると、\(x’\)の座標の値は相対的に小さくなります。
つまり、\(x’\)が小さくなると\(A’_x\)が小さくなります。
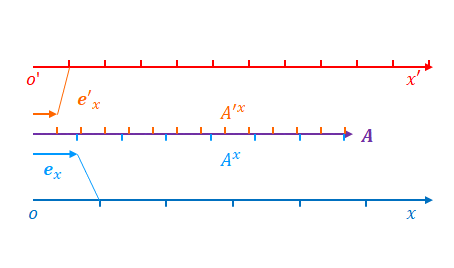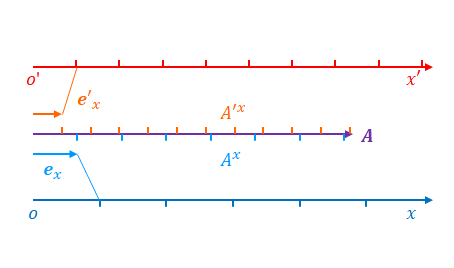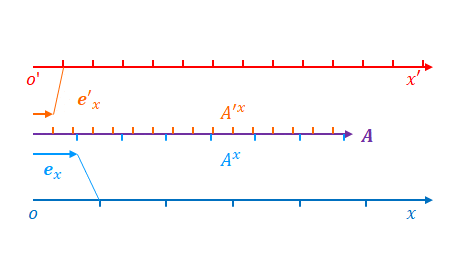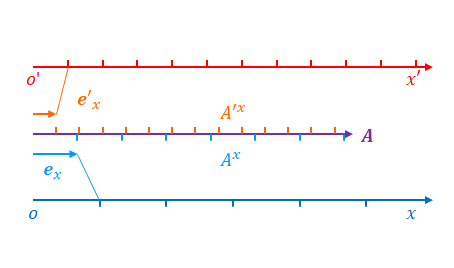
\(x’\)が小さくなるときに\(A’_x\)が小さくなれば必ず反変ベクトルというわけではありません。以下の式が成立する場合に限ります。
$$A’^x = \frac {\partial x’} {\partial x} A^x$$
このとき、\(\boldsymbol{A}\)は反変ベクトルです。
\(x\)と\(A^x\)が固定であるとして、この式をながめてください。\(x’\)の増分と\(A’^x\)が比例の関係であればこの式が成立します。
座標の目盛りが広くなるとこれに反してベクトル成分が小さくなることから反変とよばれるようです。
2.2 共変ベクトル
前節と同じように\(x\)と\(x’\)の目盛り、座標、基底ベクトル、ベクトル成分の関係を考えます。
\(x\)の目盛りは固定のまま\(x’\)の目盛りが広がったとします。
反変ベクトルの場合は\(\boldsymbol{e}’_x\)が大きくなりましたが、共変ベクトルの場合は\(\boldsymbol{e}’^{x}\)が小さくなります。
逆に\(A’_{x}\)は大きくなります。
\(x’\)の目盛りが広がれば\(x’\)は小さくなります。
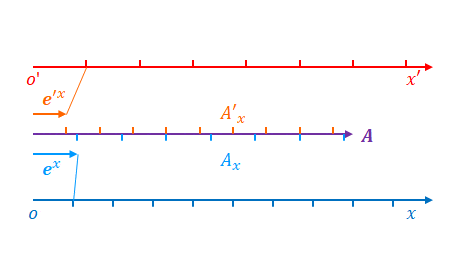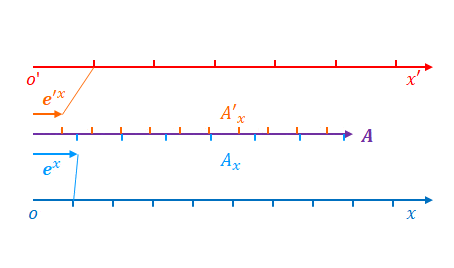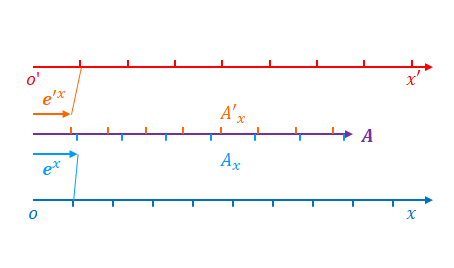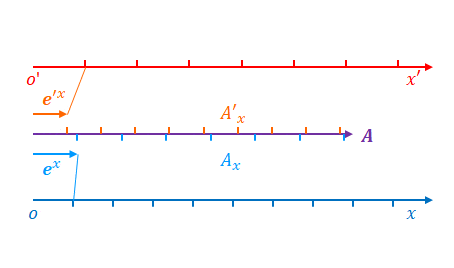
ただし、
$$A’_x = \frac {\partial x} {\partial x’} A_x$$
という式が成立するときに限り、\(\boldsymbol{A}\)は共変ベクトルです。
\(x’\)の増分と\(A’^x\)が反比例の関係であればこの式が成立します。
座標の目盛りが広くなるとこれとともにベクトル成分が大きくなることから共変とよばれるようです。
3 その他
3.1 多次元における反変ベクトル・共変ベクトル
前章では1次元の場合の定義について述べましたが、ここでは3次元に拡張してみます。
\(S\)、\(S’\)におけるベクトルを
$$\boldsymbol {A} = A^x \boldsymbol {e}_x + A^y \boldsymbol {e}_y + A^z \boldsymbol {e}_z $$
$$\boldsymbol {A’} = A’^{x} \boldsymbol {e}’_x + A’^{y} \boldsymbol {e}’_y + A’^{z} \boldsymbol {e}’_z $$
とします。
反変ベクトルが成立する条件は、
$$A’^{x} = \frac {\partial x’} {\partial x} A^x + \frac {\partial x’} {\partial y} A^y + \frac {\partial x’} {\partial z} A^z$$
$$A’^{y} = \frac {\partial y’} {\partial x} A^x + \frac {\partial y’} {\partial y} A^y + \frac {\partial y’} {\partial z} A^z$$
$$A’^{z} = \frac {\partial z’} {\partial x} A^x + \frac {\partial z’} {\partial y} A^y + \frac {\partial z’} {\partial z} A^z$$
です。それぞれの変換式について3つの項が必要である点に注意してください。
共変ベクトルが成立する条件は、
$$A’_x = \frac {\partial x} {\partial x’} A_x + \frac {\partial y} {\partial x’} A_y + \frac {\partial z} {\partial x’} A_z$$
$$A’_y = \frac {\partial x} {\partial y’} A_x + \frac {\partial y} {\partial y’} A_y + \frac {\partial z} {\partial y’} A_z$$
$$A’_z = \frac {\partial x} {\partial z’} A_x + \frac {\partial y} {\partial z’} A_y + \frac {\partial z} {\partial z’} A_z$$
です。
3.2 基底ベクトルの共変・反変
ここまで、ベクトルの共変・反変の定義について話してきましたが、同様に基底ベクトルについても共変・反変を定義できます。
再び1次元について考えてみましょう。
座標の目盛りが広がったときにベクトル成分\(A’^x\)が小さくなると反変である、と述べました。このとき、基底ベクトル\(\boldsymbol {e}’_x\)は大きくなっています。つまり、ベクトルが反変であるとき、基底ベクトルは共変です。
これを式にして確認します。
反変の定義
$$A’^x = \frac {\partial x’} {\partial x} A^x$$
ベクトル・ベクトル成分・基底ベクトルの関係
$$\boldsymbol{A}=A’^x \boldsymbol {e}’_x = A^x \boldsymbol {e}_x $$
の2式より
$$\boldsymbol {e}’_x = \frac {\partial x} {\partial x’} \boldsymbol {e}_x$$
の関係が得られます。共変ベクトルの定義と同じ形になることが確認できました。
次に\(A_x\)が共変であった場合についてです。
座標の目盛りが広がると\(A’_x\)は小さくなりますが\(\boldsymbol{e}^x\)は大きくなります。したがって\(A_x\)が共変であれば\(\boldsymbol{e}^x\)は反変です。
式で確認します。
$$A’_x = \frac {\partial x’} {\partial x} A_x$$
$$\boldsymbol{A}=A’_x \boldsymbol {e}’^x = A_x \boldsymbol {e}^x $$
より、
$$\boldsymbol {e}’^x = \frac {\partial x’} {\partial x} \boldsymbol {e}^x$$
の関係が得られます。反変ベクトルの定義と同じ形になることが確認できました。
3.3 なぜ勾配は共変ベクトル?
反変ベクトルの例を挙げることは簡単だと思います。例えば、\(t=0\)の瞬間に\(\boldsymbol{X}=(x,y,z)\)という位置ベクトルをローレンツ変換する場合、反変ベクトルの条件式に適用すれば反変ベクトルであることがわかります。
では共変ベクトルにはどのようなものがあるでしょう。
空間\(x\)のいたるところでスカラーが存在し、その値が\(x\)によって変わる場合、これをスカラー場とよびます。ここではスカラー場を\(\phi\)とします。スカラー場の勾配は以下のように\(x\)についての偏微分を使ってベクトルとして表されます。
$$\frac {\partial \phi} {\partial x}\boldsymbol {e}^x$$
ベクトル成分は以下です。
$$\frac {\partial \phi} {\partial x}$$
これを図で考えてみましょう。
下の図はグラフとして表しています。これまでの図とは見方が異なるので注意してください。
灰色はスカラー場、紫色は勾配です。勾配のベクトル成分は\(\boldsymbol{e}_x\)や\(\boldsymbol{e}_x’\)によって決まります。横軸は\(x\)、\(x’\)です。
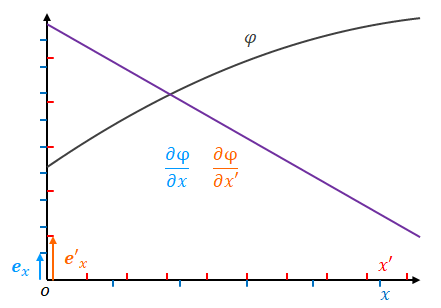
線で挟まれた区間に注目してください。\(x’\)上の距離を\(\Delta x’\)、その区間における\(\phi\)の増分を\(\Delta \phi\)とします。
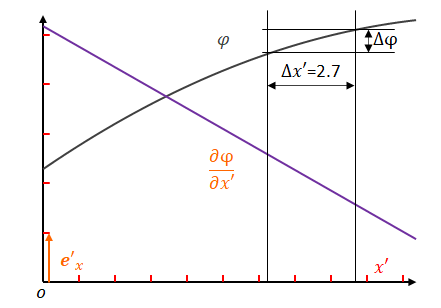
\(x\)の目盛りをグラフ上で固定したまま\(x’\)の目盛りを広げます。\(\Delta x’\)の値は小さくなります。しかし\(\Delta \phi\)は変わりません。したがって勾配は大きくなります。勾配が大きくなるというのはベクトル成分が大きくなるということです。したがって基底は小さくなります。
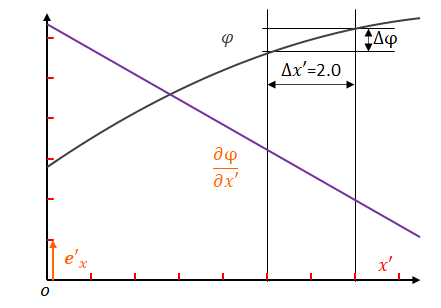
目盛りが広がると勾配が大きくなるということは、スカラー場の勾配は共変ベクトルです。
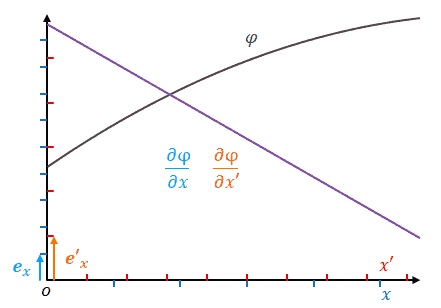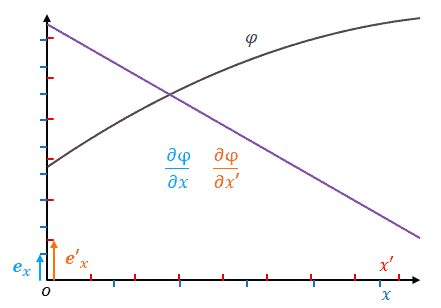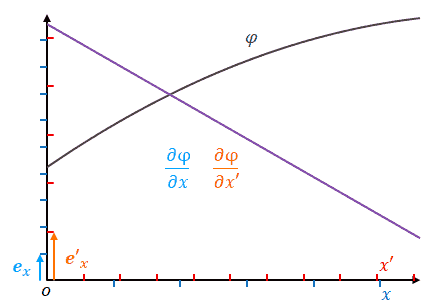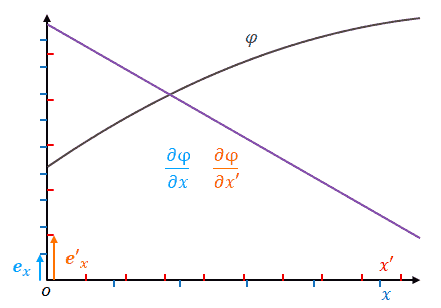
式で確認しましょう。
ベクトル成分
$$\frac {\partial \phi} {\partial x}$$
が座標変換によってどのように変化するかを考えてみます。上の式の\(x\)を\(x’\)に置き換え微分のチェーンルールを使うと、
$$\frac {\partial \phi} {\partial x’}=\frac {\partial x} {\partial x’} \frac {\partial \phi} {\partial x}$$
と表されます。
これは共変ベクトルの条件の式そのものです。スカラー場の勾配は共変ベクトルであることが確認できました。
4 まとめ
・以下が成立する場合、\(\boldsymbol{A}\)を反変ベクトルとよびます(1次元の場合です)。
$$A’^x = \frac {\partial x’} {\partial x} A^x$$
・以下が成立する場合、\(\boldsymbol{A}\)を共変ベクトルとよびます(1次元の場合です)。
$$A’_x = \frac {\partial x} {\partial x’} A_x$$
・\(\boldsymbol{A}\)が反変ベクトルの場合、\(x\)の目盛りが固定で\(x’\)の目盛りが広がるとき、\(A’_x\)が小さくなります。
・\(\boldsymbol{A}\)が共変ベクトルの場合、\(x\)の目盛りが固定で\(x’\)の目盛りが広がるとき、\(A’_x\)が大きくなります。
・反変ベクトルの基底ベクトルは共変、共変ベクトルの基底ベクトルは反変です。
