特殊相対性理論では、時間と空間を1つにまとめた4元ベクトルを使用します。また、速度などの4元ベクトルは前ページで述べた「固有時」について微分をするよう定義されています。この4元ベクトルについて説明します。
区別のため、本ページでは以下のように使い分けます。
・4元ベクトルを大文字の太字、3次元ベクトルを小文字の太字で表します。
・特殊相対性理論では一般的には整数を添え字とした表記をしますが、ここでは\(t\)、\(x\)など時間・空間を意味する文字を使って表します。
・系の相対速度により決まるローレンツ因子を\(\gamma_v\)とします。それ以外(\(\gamma\)のように添え字がないものや\(\gamma_{a1}\)のように\(v\)以外の添え字のもの)は物体の速度により決まるローレンツ因子とします。
1 4元ベクトルの定義
1.1 4元ベクトルとは
改めて、ガリレイ変換とローレンツ変換の違いを確認しましょう。
ガリレイ変換:
$$t^{\prime}=t$$
$$x^{\prime} = x – vt$$
$$y^{\prime}=y$$
$$z^{\prime}=z$$
ローレンツ変換:
$$t^{\prime}=\gamma_v \left(t-\frac{vx}{c^2} \right)$$
$$x^{\prime}=\gamma_v (x-vt)$$
$$y^{\prime}=y$$
$$z^{\prime}=z$$
両者の時間の変換の違いに注目してください。
ガリレイ変換では、空間の座標によって時間の進み方が変わることはありません。
一方、ローレンツ変換では、時間は空間に依存します。つまり、時間の進み方は位置によって異なります。空間座標に何らかの演算を行う場合、一般的には時間座標にも演算が必要になります。
そこで、相対性理論では時間と空間を1つのベクトルとしてまとめて扱います。これを4元ベクトルとよびます。
ニュートン力学同様、3次元の空間のみのベクトルも使いますが、これは3次元ベクトルとよび区別します。
本章では位置(空間)・速度・運動量・加速度・力の3次元ベクトルと4元ベクトルの定義について述べます。また、両者の関係についても少し説明します。
1.2 位置ベクトルの定義
3次元位置ベクトルは
$$\boldsymbol{x}=(x,y,z)$$
でしたが、4元位置ベクトルはこれに\(ct\)を追加し、
$$\boldsymbol{X}=(ct,x,y,z)=(ct,\boldsymbol{x}) $$
です。
\(t\)は時間ですが、\(ct\)の次元は距離(空間)なので、他の要素と次元は同じです。
ここでは、位置ベクトルとして\(\boldsymbol{x}\)、\(\boldsymbol{X}\)、を使っていますが、要素の1つである\(x\)だけを指しているわけではありません。\(y\)、\(z\)なども含むので注意してください。
1.3 速度の定義
4元ベクトルは空間の次元だけではなく、これらを時間について微分したり係数が追加された物理量についても定義されます。その1つが4元速度です。
「4元位置ベクトル」は「4元位置」と表現されることはあまりないようですが、速度などは「ベクトル」を省略することが多いようなので、ここでもそれに従います。
3次元速度は
$$\boldsymbol{u}=\frac { d \boldsymbol{r} } { dt }$$
です。
4元速度では\(dt\)ではなく\(d\tau\)を使い
$$\boldsymbol{U}=\frac { d \boldsymbol{X} } { d\tau }$$
です。
$$\frac{dt}{d\tau} =\gamma$$
なので、4元速度を3次元速度を用いて表すと、
\begin{align*}
\boldsymbol{U}&= \frac { d \boldsymbol{X} } { d\tau } = \gamma \frac { d \boldsymbol{X} } {dt} = \gamma \left(\frac{d(ct)}{dt}, \frac{d\boldsymbol{x}}{dt} \right) = \gamma \left(c, \boldsymbol{u} \right)
\end{align*}
となります。
1.4 運動量の定義
3次元運動量は、
$$\boldsymbol{p}= \gamma m\boldsymbol{u}$$
です。
「特殊相対性理論3(運動量)」で、相対性理論においては運動量の定義が変わると述べましたが、その定義がこれです。
4元運動量は、
$$\boldsymbol{P} = m \boldsymbol{U} = m \frac { d\boldsymbol{X} } {d\tau}$$
です。
$$E=\gamma m c^2$$
を変形した
$$\frac {E} {c} = \gamma m c$$
と、
$$ \gamma m \frac { d \boldsymbol{x} } { dt }= \gamma m\boldsymbol{u}= \boldsymbol{p}$$
の関係より、4元運動量を3次元運動量を用いて表すと、
$$\boldsymbol{P} = m \frac { d\boldsymbol{X} } {d\tau}=\left( m\frac { d(ct) } {d\tau} , m\frac { d\boldsymbol{x} } {d\tau} \right)
= \left(\gamma mc , \gamma m \frac { d\boldsymbol{x} } {dt} \right)
=\left( \frac {E} {c}, \boldsymbol {p} \right)
$$
となります。
1.5 加速度の定義
特殊相対性理論は慣性系間の現象に関する理論です。慣性系とは加速度がない系のことですが、特殊相対性理論では加速度を扱うことが可能であるとされています。
その場合、「微小な時間の中ではそれぞれの系は等速直線運動を行っているが、次の微小な時間ではその速度が切り替わる」と考えます。力についても同様です。
3次元加速度は、
$$\boldsymbol{a} = \frac { d \boldsymbol{u} } { dt } = \frac { d^2 \boldsymbol{x} } { dt^2 }$$
4元加速度は、
$$\boldsymbol{A} = \frac {d\boldsymbol {U}} { d\tau } = \frac { d^2 \boldsymbol{X} } { d\tau^2 }$$
です。
4元加速度を3次元加速度だけで表すことはできないと思いますが、3次元速度を含めて表すと、
$$\boldsymbol{A} = \left( \gamma^4 \frac { \boldsymbol{u} \cdot \boldsymbol{a} } { c }, \gamma^4 \frac { \left( \boldsymbol {a} \cdot \boldsymbol {u} \right) \boldsymbol {u} } {c^2} + \gamma ^2 \boldsymbol {a} \right)$$
と、かなり複雑になります。導出過程は省略します。
1.6 力の定義
3次元力は
$$\boldsymbol{f} = \frac { d \boldsymbol {p } } {dt} = \frac { d \left( \gamma m \boldsymbol{u} \right) } {dt}$$
4元力は
$$\boldsymbol{F} = \frac { d \boldsymbol {P} } {d\tau} = m \frac {d\boldsymbol {U}} { d\tau } = m \frac {d^2 \boldsymbol {X}} { d\tau^2 } $$
です。
4元力を3次元力などを用いて表すと、
\begin{align}
\boldsymbol{F} &= \frac { d \boldsymbol {P} } {d\tau}
=\frac{d}{d\tau}\left(\frac{E}{c}, \boldsymbol{p}\right)
=\gamma \left(\frac{dE}{d(ct)}, \frac {d\boldsymbol{p}} {dt} \right)
=\gamma \left(\frac{ \boldsymbol{f} \cdot \boldsymbol{u} } {c}, \boldsymbol{f} \right)
\end{align}
となります。
2 座標変換
2.1 ローレンツ変換
3次元位置ベクトルと時間の座標変換(ローレンツ変換)は以下でした。
$$t’=\gamma_v \left(t-\frac{vx}{c^2} \right)$$
$$x’=\gamma_v (x-vt)$$
$$y’=y$$
$$z’=z$$
これらを以下の式に代入すると、
$$\boldsymbol{X}=(ct,x,y,z) $$
$$\boldsymbol{X’}=(ct’,x’,y’,z’) $$
以下のように4元位置ベクトルの変換式が得られます。
$$X’_t= \gamma_v \left( X_t – \frac {X_x v} {c} \right) $$
$$X’_x = \gamma_v \left( X_x – \frac {X_t v} {c} \right) $$
$$X’_y = X_y $$
$$X’_z = X_z $$
2.2 速度の座標変換
3次元速度の座標変換(速度の合成則)は以下でした。
$$u’_x = \frac {u_x – v } {1 – \frac {u_x v} {c^2} } $$
$$u’_y = \frac{u_y }{\gamma_v \left(1-\frac{u_x v}{c^2}\right)}$$
$$u’_z = \frac{u_z }{\gamma_v \left(1-\frac{u_x v}{c^2}\right)}$$
4元速度の変換は以下のように4元位置ベクトルより導くことができます。
$$X’_t= \gamma_v \left( X_t – \frac {X_x v} {c} \right) $$
の両辺を\(d\tau\)で割ると、
$$\frac {X’_t} {d\tau} = U’_t = \gamma_v \left( \frac {X_t} {d\tau} – \frac {X_x v} {c d\tau} \right) = \gamma_v \left( U_t – \frac {U_x v} {c} \right) $$
同様に
$$\frac {X’_x} {d\tau} = U’_x = \gamma_v \left( \frac {X_x} {d\tau} – \frac {X_t v} {c d\tau} \right) = \gamma_v \left( U_x – \frac {U_t v} {c} \right) $$
\(y\)と\(z\)の要素は変わらず
$$U’_y = U_y $$
$$U’_z = U_z $$
です。
\(d\tau\)がローレンツ不変であるためにこのような簡単な関係になります。
2.3 運動量の座標変換
詳細を省略しますが、3次元運動量の座標変換は以下です。
$$p’_x = \gamma_v \left( p_x – \frac {E v } {c^2} \right) $$
$$p’_y = p_y$$
$$p’_z = p_z$$
4元運動量の座標変換は4元速度と同様に\(\boldsymbol{X}\)の微分より導出できます。あるいは単に\(\boldsymbol{U}\)
$$P’_t= \gamma_v \left( P_t – \frac {P_x v} {c} \right) $$
$$P’_x = \gamma_v \left( P_x – \frac {P_t v} {c} \right) $$
$$P’_y = P_y $$
$$P’_z = P_z $$
2.4 加速度の座標変換
3次元加速度の座標変換は以下のようにかなり複雑です。
$$a’_x = \frac {a_x} {\gamma_v^3 \left( 1 – \frac { u_x v } { c^2 } \right)^3}$$
$$a’_y = \frac {a_y} {\gamma_v^2 \left( 1 – \frac { u_x v } { c^2 } \right)^2} + \frac {a_x \frac { u_y v } { c^2 }} {\gamma_v^2 \left( 1 – \frac { u_x v } { c^2 } \right)^3}$$
$$a’_z = \frac {a_z} {\gamma_v^2 \left( 1 – \frac { u_x v } { c^2 } \right)^2} + \frac {a_x \frac { u_z v } { c^2 }} {\gamma_v^2 \left( 1 – \frac { u_x v } { c^2 } \right)^3}$$
4元加速度の座標変換は、4元位置ベクトルから4元速度を求めた手順と同じように4元速度から求めることができます。
$$A’_t= \gamma_v \left( A_t – \frac {A_x v} {c} \right) $$
$$A’_x = \gamma_v \left( A_x – \frac {A_t v} {c} \right) $$
$$A’_y = A_y $$
$$A’_z = A_z $$
2.5 力の座標変換
3次元力の座標変換も複雑です。
$$f’_x = f_x – \frac { \frac {v} {c^2} \left( f_y u_y + f_z u_z \right) } { 1 – \frac {u_x v} {c^2} }$$
$$f’_y = \frac { f_y } { \gamma_v \left( 1 – \frac {u_x v} {c^2} \right) }$$
$$f’_z = \frac { f_z } { \gamma_v \left( 1 – \frac {u_x v} {c^2} \right) }$$
4元力の座標変換も4元加速度などと同様、4元運動量を時間微分することにより求められます。また、後述しますが4元力の場合は単に4元加速度と質量の積でもあります。
$$F’_t= \gamma_v \left( F_t – \frac {F_x v} {c} \right) $$
$$F’_x = \gamma_v \left( F_x – \frac {F_t v} {c} \right) $$
$$F’_y = F_y $$
$$F’_z = F’_z $$
3 4元ベクトルによる運動法則
3.1 運動量保存則
「特殊相対性理論3(運動量)」では、粒子の弾性衝突の例について運動量保存則が慣性系によらず成立することを確認しました。そのページでは質量、速度、\(\gamma\)を使いましたが、これらを4元運動量に置き換えて表すこともできます。
まず以下のように定義します(「特殊相対性理論3(運動量)」のページでは\(z\)方向の要素はありませんでしたが、ここでは4元ベクトルになるよう追加しています)。
$$\boldsymbol{P}_{a1}=\left( \frac {E_{a1}} {c}, \gamma_{a1} m u_{a1x}, \gamma_{a1} m u_{a1y} , \gamma_{a1} m u_{a1z} \right)$$
\(b1\)、\(a2\)、\(b2\)なども同様に定義します。また、\(S’\)の物理量も同様に定義します。
そして
$$\boldsymbol {P}_{a1} + \boldsymbol {P}_{b1} = \boldsymbol {P}_{a2} + \boldsymbol {P}_{b2} $$
が成立する場合、
$$\boldsymbol {P’}_{a1} + \boldsymbol {P’}_{b1} = \boldsymbol {P’}_{a2} + \boldsymbol {P’}_{b2} $$
が成立するということがいえます。
各項の0番目の要素はエネルギー保存則(ただし各項を\(c\)で割っています)1-3番目の要素は運動量保存則を示している点に注意してください。
この関係は、4元運動量の座標変換を使うことでも確認できます。
まず、以下のようにベクトルを定義します。
\(S\)における運動量
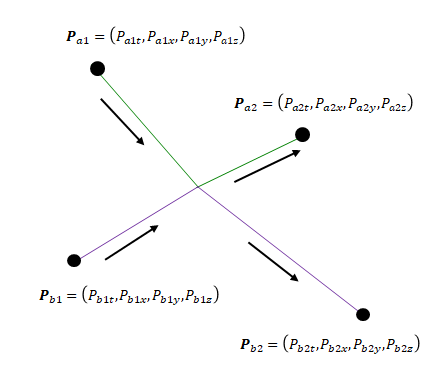
\(S’\)における運動量
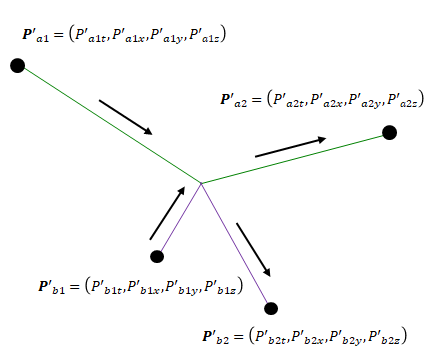
そして、
$$\boldsymbol {P}_{a1} + \boldsymbol {P}_{b1} = \boldsymbol {P}_{a2} + \boldsymbol {P}_{b2} \tag{1}$$
の関係にある場合、
$$\boldsymbol {P’}_{a1} + \boldsymbol {P’}_{b1} = \boldsymbol {P’}_{a2} + \boldsymbol {P’}_{b2} \tag{2}$$
が成立することを確認します。
4元運動量の座標変換は以下です。
$$P’_t= \gamma_v \left( P_t – \frac {P_x v} {c} \right) \tag{3}$$
$$P’_x = \gamma_v \left( P_x – \frac {P_t v} {c} \right) \tag{4}$$
$$P’_y = P_y \tag{5}$$
$$P’_z = P_z \tag{6}$$
\( (3)-(6) \)を\( (2) \)にあてはめます。
\begin{align}
& \gamma_v \left( P_{a1t} – \frac {P_{a1x} v} {c} \right) + \gamma_v \left( P_{b1t} – \frac {P_{b1x} v} {c} \right) \\
=& \gamma_v \left( P_{a2t} – \frac {P_{a2x} v} {c} \right) + \gamma_v \left( P_{b2t} – \frac {P_{b2x} v} {c} \right) \tag{7}
\end{align}
\begin{align}
&\gamma_v \left( P_{a1x} – \frac {P_{a1t} v} {c} \right) + \gamma_v \left( P_{b1x} – \frac {P_{b1t} v} {c} \right) \\
= &\gamma_v \left( P_{a2x} – \frac {P_{a2t} v} {c} \right) + \gamma_v \left( P_{b2x} – \frac {P_{b2t} v} {c} \right) \tag{8}
\end{align}
$$P_{a1y} + P_{b1y} = P_{a2y} + P_{b2y} \tag{9}$$
$$P_{a1z} + P_{b1z} = P_{a2z} + P_{b2z} \tag{10}$$
これらの等式が成立することを確認します。
\( (7) \)をとばしてまず\( (8) \)から確認します。
\( (8) \)を2つの等式が成り立つものとして分けます。
$$\gamma_v P_{a1x} + \gamma_v P_{b1x} = \gamma_v P_{a2x} + \gamma_v P_{b2x}$$
$$- \frac {\gamma_v P_{a1t} v} {c} – \frac {\gamma_v P_{b1t} v} {c} = – \frac {\gamma_v P_{a2t} v} {c} – \frac {\gamma_v P_{b2t} v} {c}$$
共通の係数を除いて
$$P_{a1x} + P_{b1x} = P_{a2x} + P_{b2x} \tag{11}$$
$$P_{a1t} + P_{b1t} = P_{a2t} + P_{b2t} \tag{12}$$
となります。\( (11) \)は\( (1) \)の各項の1番目、\( (12) \)は0番目の要素による等式なのでこれらは成立します。
次に\( (7) \)です。これは\(S’\)におけるエネルギー保存則なので当然成立すると考えてもよいのですが、\( (6) \)と同じように式を分解して確認することもできます。
\( (9) \)、\( (10) \)はそれぞれ\( (1) \)の2番目、3番目の要素による等式なのでこれらも成立します。
以上より\( (1) \)の関係にあるなら\( (2) \)が成立することが確認できました。
3.2 ニュートンの第2法則
ニュートンの第2法則
$$\boldsymbol {f} = m \boldsymbol {a} $$
は、特殊相対性理論においても、成立するのでしょうか。
3次元ベクトルの場合、以下を見比べてわかるように成立しません。
$$\boldsymbol{a} = \frac { d \boldsymbol{u} } { dt }$$
$$\boldsymbol{f} = \frac { d \boldsymbol {p } } {dt} = \frac { d \left( \gamma m \boldsymbol{u} \right) } {dt} $$
では、
$$\boldsymbol{f}=\gamma m \boldsymbol {a}$$
となるかというとそうでもありません。
\(\boldsymbol{f}\)には\(\gamma\)と\(\boldsymbol{u}\)が含まれます。これらはそれぞれ時間によって変化します。その積を微分するので、積の微分公式を適用する必要があります。つまり、項が複数に分かれます。しかも\(\gamma\)の導関数は簡単な形式ではありません。このように複雑な式になるので3次元ベクトルの場合はニュートンの第2法則は成立しません。
では、4元ベクトルではどうでしょう。
$$\boldsymbol{F}=\frac {d\boldsymbol{P}} {d\tau} = m\frac {d\boldsymbol{U}}{d\tau}=m\boldsymbol{A}$$
の関係により、\(S\)においてニュートンの第2法則は成立します。\(S’\)においても、
$$\boldsymbol{F’}=\frac {d\boldsymbol{P’}} {d\tau} = m\frac {d\boldsymbol{U’}}{d\tau}=m\boldsymbol{A’}$$
なので、慣性系によらず成立することがわかります。
4 まとめ
・ガリレイ変換では、時間の変換は空間に依存しませんでしたが、ローレンツ変換では時間の変換は空間によって変わります。そこで特殊相対性理論では時間と空間をまとめた4元ベクトルを使います。
・4元速度などの定義における時間微分は\(dt\)ではなく\(d\tau\)を使います
・\(d\tau\)を使うことにより一部の物理量の定義や物理法則は慣性系によらない形式で表すことができます。
・以下に定義などをまとめました。
