学校の音楽の時間に習った曲は、ほとんどが平均律(十二平均律)という音律に基づいて作られています。オリコンやビルボードなどのヒットチャートに登場するような曲もこれらにならっています。
(1)平均律とは
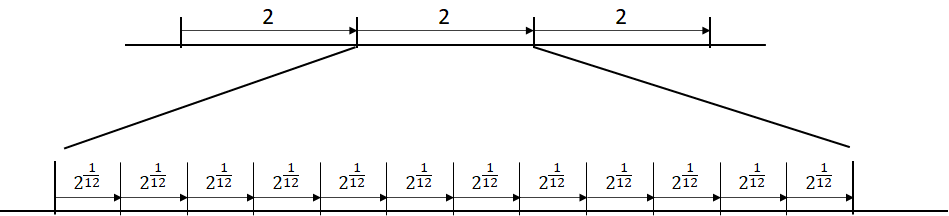
平均律とは、隣り合う音の周波数比を全て等しくした音律です。この音が十二平均律の場合、1オクターブに12あります。
1オクターブにある音は7ではないかと思われるかもしれませんが、ここでは半音の数のことです。5を足して12です。
1オクターブの周波数比は2です。つまり1オクターブ上がると周波数は2倍になります。

したがって、隣り合う音との周波数比は21/12です。
(2)音階について
平均律の長所と短所の前に音階について簡単に説明します。説明は簡単ですが、理解するには少しややこしいかもしれません。
1オクターブ内の各音階はアルファベット(または「イロハ」)で表されます。半音高い音は♯がつきます(半音下げた♭でも表すことができます)。
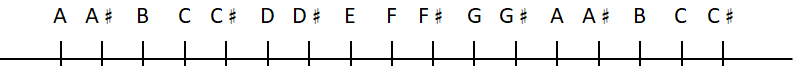
ABCではなく「ドレミ」を使わないのかと思われるかもしれませんが、日本では一般的に、絶対的な音の高さはABC、主音に対する相対的な高さはドレミを使います。
主音は長音階の場合ド、短音階の場合ラです。
ハ長調の場合は主音がCです(Aがイ、Cがハと同じです)。
ハ長調とニ長調の違いを確認ください。

(3)平均律の短所
隣り合う音の周波数比が一定というところがなんとなく合理的に思えますが、一つ短所があります。
和音です。
一般的に、人間の耳は、和音の周波数比が単純な整数であった場合、心地よく感じます。単純な整数比でない場合は違和感をもちます。
しかし十二平均律は2の12乗根を最小単位にしているので、和音の周波数比は単純ではありません。例えば、完全5度という和音(CとGなど)の比は1.5ではなく1.498と、多少ずれています。他も同様です。
| 音程 | 半音の数 | 周波数比 |
| 短三度 | 3 | 1.189 |
| 長三度 | 4 | 1.260 |
| 完全四度 | 5 | 1.335 |
| 完全五度 | 7 | 1.498 |
| 長六度 | 9 | 1.682 |
(4)純正律
和音の周波数比のずれがない音律もあります。純正律であれば和音が整数比になります。
| 音程 | 半音の数 | 平均律周波数比 | 純正律周波数比 |
| 短三度 | 3 | 1.189 | 6/5=1.200 |
| 長三度 | 4 | 1.260 | 5/4=1.250 |
| 完全四度 | 5 | 1.335 | 4/3=1.333 |
| 完全五度 | 7 | 1.498 | 3/2=1.500 |
| 長六度 | 9 | 1.682 | 5/3=1.667 |
ただし、純正律は隣り合う音の周波数比は一定ではありません。これが問題となります。
(5)純正律の短所
純正律には大きな問題点があります。転調に向いていないことです。
転調とは曲の途中で主音を変えることです。例えば、ハ長調からニ長調に変えるような場合です(上の図を参照ください)。
平均律の場合、音階が等比であるため、転調をしても和音の周波数比が一定です。しかし、純正律は隣り合う音の周波数比が一定ではありません。ある調では和音が単純な整数比になるよう楽器を調律してあったとしても、転調すると不協和音になってしまいます。
転調はよく使われます。特殊な楽器でない限り、純正律では転調に対応することが困難です。したがって平均律が使われることが多いのです。
