帰省や行楽のシーズンともなると、必ずといっていいほど渋滞の状況が報道されます。なぜ渋滞が発生するのでしょう。考えるまでもなく、道路の容量に対し車が多すぎるからですね。
ところが、道路を増やすとかえって到着までの時間が増える現象があります。これを発見した科学者の名にちなみ「ブライスのパラドックス」とよばれます。
直感に反するのですが、現実にもこのような現象が起きているとされており、このパラドックスが存在することは間違いなさそうです。なぜそうなるのか、考えてみましょう。
※ここで用いている一部の言葉については末項で補足しました。
(1)条件(道路追加前)
条件は以下の通りです。
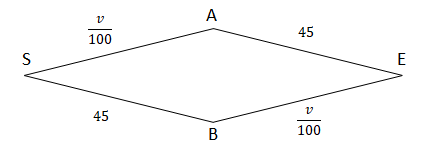
・車は全て図のSからAまたはBを経由してEに到着する。
・2通りの経路がある。
・S-BとA-E間は常にそれぞれ45分かかる。
・S-AとB-E間は交通量(1時間あたり通った台数)を100で割った値(分)だけかかる。式は以下。
$$t = \frac {v}{100 }$$
ただし、\(t\)は区間を通る時間(分)、\(v\)は交通量(1時間あたりに通過する車の台数)とする。
(2)通過にかかる時間(道路追加前)
上記条件で各区間を通過する時間を求めましょう。
Sにおける交通量(分岐前)は4000台/時とします。
S-A-EとS-B-Eを比べてみましょう。順序は逆ではありますが、どちらも固定(45分)と従量(v/100分)の区間を1回ずつ通ります。つまり両者を通るのにかかる時間は同じはずです。交通量も同じです。
もしどちらかの経路の交通量が多いとすればその従量区間の所要時間が大きくなるので交通量が少ない経路を選ぶ車が増えます。したがって両経路の所要時間と交通量が同じになるよう保たれます。
ということは、両経路の交通量は2000台/時です。このことからS-AとB-Eを通る時間が求められます。つまり、
$$\frac{2000}{100} = 20(分)$$
です。
A-EとS-Bは前提条件の通り、45分固定です。
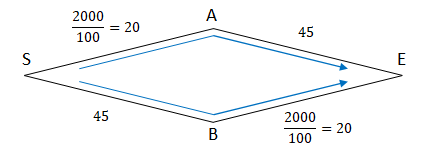
したがって、S-A-E、S-B-Eの所要時間はどちらも65分です。
(3)通過にかかる時間(道路追加後)
さて、次に道路を追加します。AとBの間です(下図参照)。このA-Bの間は双方向です。したがって通り得る経路は以下の4通りです。
・S-A-E
・S-A-B-E
・S-B-E
・S-B-A-E
Sにいる車はA/Bどちらを選ぶでしょう。前項では経路は2通りしかなくどちらを通っても同じということがわかっていました。しかし道路が追加されたことによって経路の選択肢も増えています。
SにいるドライバーはAまでの時間とBまでの時間を比較するでしょう。もし全ての車がAに向かったとしてもAまでの時間は
$$\frac{4000}{100} = 40(分)$$
です。
一方、Bまでの時間は45分です。したがって、全てのドライバーがAを選びます。S-A間の通過時間は前述の通り40分です。
次にAにいる車は直接Eへ向かう道路を選ぶでしょうか。あるいはBを通りEへ向かう経路を選ぶでしょうか。
これも先ほどの関係と同じです。A-B間の時間は0だったので無視します。A-E間は45分、B-E間は40分です。ドライバーは全てA-B-Eの経路を選びます。
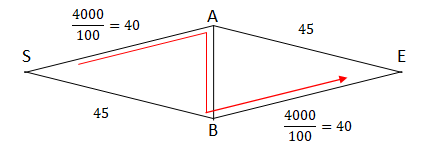
S-A間の40分とA-B-E間の40分を足して80分です。
前項では65分でした。道路が追加になっているのに遅くなっています。これがパラドックスです。
(4)パラドックスの原因1(交通量と所要時間の関係)
この現象は、理解してしまえば何ということはないのですが、意外に理解するのが簡単ではありません。じっくり考えましょう。
各経路の所要時間は交通量によって変わります。道路追加前、道路追加後について交通量を変え所要時間がどう変化するかを比較してみます。
下のグラフは横軸を交通量、縦軸を所要時間としています。
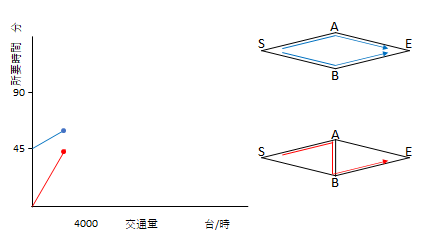
まず、交通量が0の場合を考えてみます。S-A間とB-E間の従量区間の通過時間は交通量によって決まります。交通量が0であれば通過時間は0ということになります。実際に2点間を0秒で移動することはあり得ませんが、あくまで理論上の結果として0を想定します。
道路追加前の場合はS-A-E、S-B-Eどちらも固定の区間の45分のみです。道路追加後はS-A-B-Eを通ればよいので時間は0です。
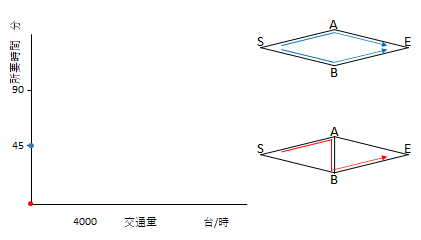
次に交通量が少し増えた場合です。従量区間の通過時間は交通量に比例します。ここで注意したいのは、道路追加前の場合、それぞれの区間の交通量はS(分岐前)の交通量の半分ということです。一方、追加後はS-A、B-Eに全ての車が通ります。
したがって、交通量の増分に対する所要時間の増え方は道路追加前後で異なります。道路追加前は道路追加後の半分です。
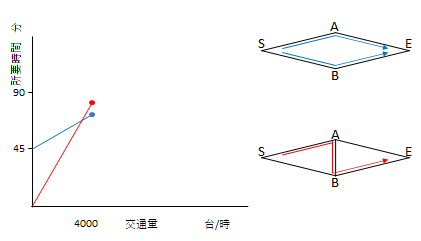
そして次がパラドックスとされる状態です。
交通量が増え続けると道路追加後の方が所要時間が長くなるという逆転現象が起きます。
さらに交通量が増えるとどうなるでしょう。
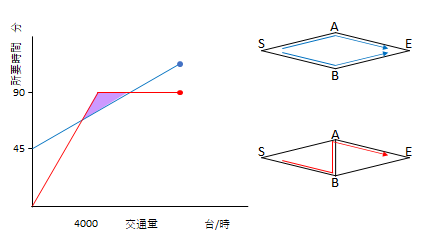
道路追加前の場合は必ず従量区間を通るので交通量の増加とともに所要時間は増えます。
道路追加後はS-B-A-Eという、固定区間のみを通ればよいので90分のまま増えることはありません。
グラフの紫で示した条件においてパラドックスが生じていることになります。
(5)パラドックスの原因2(疑問点)
・A-B間の道路が追加されても自分だけはここを通らなければよいのでは?
ページ冒頭のパラドックスを思い出してみましょう。交通量は4000台/時、道路追加前の所要時間は65分、追加後は80分です。道路追加後、自分だけは別の経路つまりS-A-B-E以外の経路を通ればよいのではないでしょうか。
しかし、以下のようにさらに遅くなります。他の車と同じようにS-A-B-Eを通るのがよいということになります。この車が固定区間を通れば、その分だけ(わずかですが)従量区間の通過時間は軽減されるでしょう。しかし自分自身には何のメリットもありません。
S-AーE:85分
S-B-E:85分
S-B-A-E:90分
・A-B間の道路が追加されても全ての車がここを通らなければよいのでは?
全てのドライバーが自発的にS-A-EまたはS-B-Eのどちらかを通ったらどうでしょう。これはA-B間の道路がないことと同じです。したがって、以下のようになります。全体としては最適の選択なのです。
S-A-E:65分
S-B-E:65分
(6)パラドックスの原因3(根本の原因)
根本の原因は何なのでしょう。
各個人にとっては合理的な行動であっても、全体としては合理的ではないということです。
Sにいるドライバーは固定の道路と従量の道路を比較します。従量の道路の通過時間が45分を超えない限り従量の道路を選びます。しかも、う回路(A-B)によって1回ではなく2回とも(S-AとB-E)従量の道路を選ぼうとします。
しかし従量の道路の交通量が大きくなると通過時間が増えます。1回は固定、もう1回は従量を通るようにした方が全体としては時間が短くなる場合があるのです。
(7)シミュレーション
さて、この現象をシミュレーションによって確かめてみましょう。
事前の説明がたくさんあります。
・デフォルト(定数)の状態で実行すると約2分かかります。設定を変えて(乱数)実行するとさらに長くなり3分近くかかります。ご了承ください。・A-B間の道路追加前(上のダイアグラム)と追加後(下のダイアグラム)があり、同時に実行します。
・環境によっては表示が遅くなる場合があります。30秒たっても散布図が更新されないようなら「軽」のボタンを押してください。散布図の横の表示が「軽20」となっていれば少し早くなるはずです。十数秒で散布図が更新される場合でも、「軽」のボタンを押せばより速く結果が表示されます。ただし若干動きは見づらくなるかもしれません。
・S-A、B-Eが従量、A-E、S-Bが固定区間です。
・ダイアグラムの丸は車です。識別しやすいよう、色をランダムに替えています。
・交通量を変えて8回実行します。
・左の棒グラフはS-E間の所要時間です。最も短い時間を示しています。青は道路追加前、赤は道路追加後です。
・右の棒グラフは各区間の通過時間です。
・散布図の縦軸は各試行の最後の瞬間のS-E間の値です。横軸は交通量です。道路追加前と追加後の差が少しでも見やすくなるよう、縦軸(所要時間)は0からではなく、ある値より開始しています。
・「定数」と「乱数」の設定があります。定数は、Sへの車の到着時間、車の速度は全て同じです。
乱数は到着時間、速度を乱数によってばらつかせています。
・道路追加後ではS・A・Bにおける各車の分岐は、先行する車の統計によって決めています。つまり基本的には通過時間の短い区間を選びます。
・ただし、無作為に長い方の区間を選ぶことがあります。定数を選んだ場合も同様です。実際、ある区間の通過時間が少しだけ他より短いからといってそちらに集中するということはないだろうという判断です。
・各試行回のはじめのうちは想定通りの値にはなりません。十分な統計が得られるまでに時間がかかるからです。しばらくすると想定通りの値を指すようになります。
・A-B間を通行する車は有限の速度にしています。可視化のためです。しかし、所要時間にはA-B間の時間は含んでいません。
・全区間、車は追い抜きを可能としています(定数の場合は関係ありませんが)。複数車線あるとお考え下さい。追い抜きを不可とすると混雑の度合いによって、想定外の遅延が発生するためです。
・「開/止」を一度押すと開始します。もう一度押すと一時停止します。初期状態「定数」の設定です。
・「乱/定」を押すと「乱数」と「定数」を切り替えます。シミュレーションは初期化し実行します。
同じ設定にて初期状態から実行する場合はこのボタンを2回押してください。
さらに注意してみていただきたいところを挙げます。実行時間が長いので、なるべく事前にお読みください。
・右棒グラフのS-AとB-Eの青と赤の関係にご注意ください。初めのうちは統計が少ないため想定の値になりませんが、しばらくすると赤の方が青より長くなるはずです。これは区間を通る交通量の違いです。理論上は2倍の関係です。
・青・赤どちらも、右棒グラフのS-AとB-E、A-EとS-Bは近い値になるはずです。赤のS-A・B-EとA-E・S-Bの関係にご注意ください。交通量とともにS-A・B-Eの時間が長くなりA-E・S-Bの時間を上回るはずです。
・道路追加後の車の流れは、交通量が少ない場合はS-A-B-Eですが、5回目あたりでS-B-A-Eに変わります。
・「乱数」の状態はばらつきが大きく傾向が把握しづらいかもしれないので、まずは「定数」をお試しください。
(8)シミュレーションの考察
2分間我慢していただけたでしょうか。以下は考察です。
・散布図が見づらいかもしれませんが、ある交通量において赤が青を逆転しているはずです。これがパラドックスの状態です。
・「定数」の場合、5回目付近以降で赤の時間が一定になっていると思います。これはS-A-B-Eではなく、S-B-A-Eの流れになっているからです。
・青は一定の傾きで増え続けています。交通量に比例して従量区間の時間が増えるからです。このシユレーションでは実施していませんが、このまま交通量を増やし続けると、再び青の所要時間が赤より長くなります。
・4回目付近で赤の時間が短くなっているかもしれません。交通量が少ない場合はほとんどの車がS-A-B-Eを選び、結果は安定しているのですが、4回目付近では他の経路の時間と拮抗しており、頻繁に経路が切り替わることがあります。過渡的な状態では従量区間の通過時間が敏感に反応しやすくこのような結果になっています。
・ここで申すまでもなく、実際には車は一定の間隔で到着しないし、速度もバラバラです。このシミュレーションの「定数」は、あくまでパラドックスを確認するためのもので、現実とは異なります。実際の状態に少しでも近づけるために「乱数」を実行できるようにしてあります。やはり「定数」に比べて結果がばらつきます。しかも実際にはもっと到着間隔も速度もばらつくはずです。ドライバーの経路の選択も曖昧でしょう。現実に車の所要時間を正確に予測することはなかなか難しそうです。しかしこのような条件下(固定の区間と従量の区間がある場合)であれば逆転現象が起こりえるだろうということは理解できるかと思います。
(9)まとめ
・ブライスのパラドックスとは、う回路を追加することによってかえって所要時間が長くなる現象です。直接の原因は、全てのドライバーがう回路を使って、交通量によって時間が変わる道路を2回通ろうとすることによってこの区間交通量が増えるところにあります。
・根本の原因は、個人にとっての合理的な行動が全体としてみた場合には最適ではない、というところにあります。似たような概念を示す言葉として、経済学では合成の誤謬(ごうせいのごびゅう)があります。ミクロの視点では正しいことがマクロの視点では正しくなくなってしまうような現象を指します。例えば、個人が消費を削減し貯蓄を増やした場合、消費が減ることによって全体としては所得が減ってしまうというような場合です。経済学以外でもいろいろありそうです。部屋に大勢人がいる状態で、突然速やかに出ないといけないような場合、出口に人が殺到すると押し合いになってかえって時間がかかるそうです。これも同様の現象といえるでしょう。
・このパラドックスの前提として、「通過時間が交通量に比例する道路」(ここでは「従量区間」)があるとしています。実際にこのような道路があるのでしょうか。ここで取り上げたような単純なトポロジーであれば通過時間が交通量に鋭敏に反応するところはイメージしにくいと思います。しかし、一般道では交差点も信号もあります。交通量が多いほど、発進してから車間距離を確保している間に次の信号待ちになる確率が高くなるかもしれません。信号待ちの時間も長くなるでしょう。このような状態を想定しているのではないでしょうか。
・では「常に通過時間が一定の道路」(ここでは「固定区間」)とはどのような道路でしょうか。交通量が増えても通過時間が変わらないということは車線の数が多い、信号待ちが少ない、ということでしょうか。それでもある程度時間がかかるのは距離が長いからでしょう。
(10)補足:ここで用いた言葉
本ページで用いた言葉について説明します。便宜的に私が使っているだけであって、一般的に通用する言葉ではないかもしれないのでご注意ください。
・区間:S・A・B・Eのうち、隣接する2点の間の道路。
・経路:SからEまでの間に通る区間の組み合わせ。
・S-A:SとAの間の区間。他も同様。
・S-A-E:SからAを通ってEに到着する経路:他も同様。
・所要時間:SからEまでにかかる時間。
・通過時間:区間の端から端までにかかる時間。
・交通量:単位時間あたりに到着・通過する車の台数。
・固定区間:交通量にかかわらず通過時間が一定の区間。
・従量区間:交通量によって通過時間が変わる区間。
・道路追加前:A-B間に道路がない状態。
・道路追加後:A-B間に道路がある状態。
