パスカルの原理を覚えているでしょうか。液体などが入った容器のある面におもりなどを載せると別の面の圧力も変わります。中学生のときに、これを求める問題などを解きましたね。
しかしこのときに触れられていない条件があります。容器の面におもりなどを載せなくても液体には重力がかかっています。重力の影響はどう考えればよいのでしょうか。
(1)パスカルの原理とは?
以下がパスカルの原理の定義です。
「密封された流体の一点に力を加えるとその圧力は流体全体に等しく伝わる。」
補足します。
・流体とは液体や気体のことです。流れていなくても流体とよびます。
・流体は静止している必要があります。流体が動いていると圧力は一様にはなりません。
・圧力とは単位面積当たりの力です。流体容器の壁面に対して垂直に圧力がかかります。
・重力の影響はないものとします。
(2)流体内で圧力はどのように伝わる?
重力について考える前に、パスカルの原理が想定する「密封された流体」とは何かを考えます。
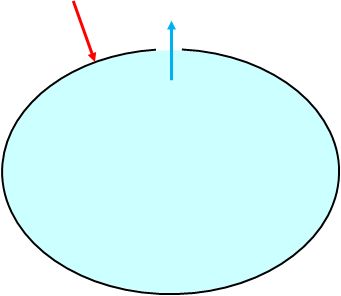
開口部のある容器に水が入っているところを想像してみましょう。
外から容器を押すと流体は外へ逃げていきます。
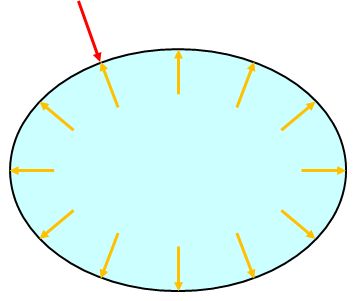
密閉されている場合はどうでしょう。流体内で力が加わると圧力が強いところから弱いところへ伝播します。容器の壁で押し返され、圧力が全体に波及するはずです。こうして容器内で圧力が均一になるのです。
(3) 流体内で重力はどう作用する?
パスカルの原理では流体内にはすべて同じ圧力が生じることを示していますが、実際には重力があれば低いところほど強い圧力になるはずです。何が違うのでしょう。
パスカルの原理では流体の1点に力が加わった場合の圧力の伝わり方を示しています。しかし重力がある場合、力はすべての場所にかかります。これをパスカルの原理に従ってどう伝播するかを考えるのは簡単ではなさそうです。
こう考えてみましょう。
容器の中に水が入っています。

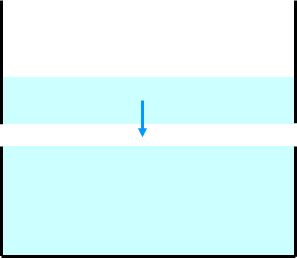
容器と水をある高さで切ります。下側の水は底面と側面を容器で支えられているので力は平衡を保ちますが、上側の水は落ちようとします。重力によるものです。
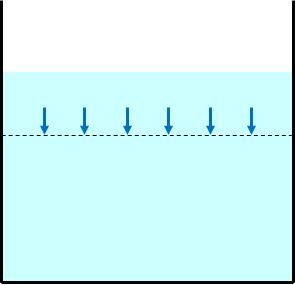
戻します。線の位置ではここより上の水の重さの分だけ圧力が生じていることになります。
圧力は容器に対して垂直にかかります。
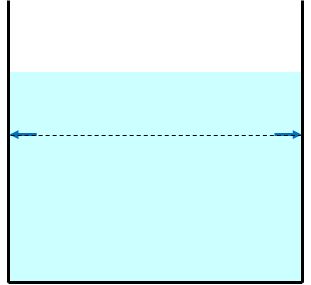
容器を切断する位置を変えても同じように容器に対して圧力がかかります。。
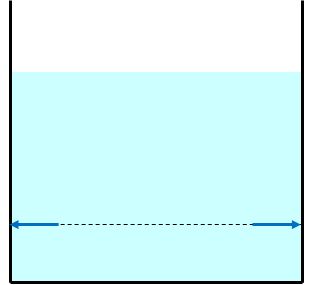
ただし、下にいくほど圧力は大きくなります。
(4)重力がある場合、パスカルの原理は成立しない?
中学校で出題された問題を思い出してみましょう。例えば「A(下図)に力を加えるとBの面に生じる力はどれだけか」というような問題があったはずです。これらの問題は重力がない場合を想定しているのでしょうか。
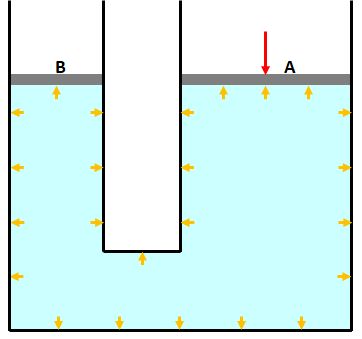
そうでもありません。重力と外部からの力を分けて考えればよいのです。
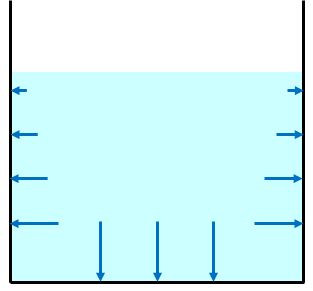
下の図は重力だけがかかっている状態です。
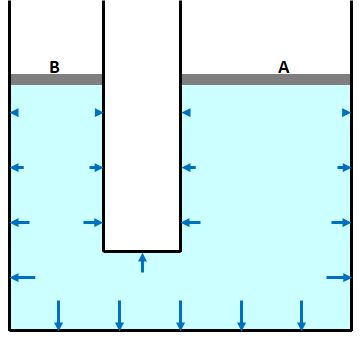
ここに外部から力が加わったとします。流体内の圧力は変化します。この変化した分がパスカルの原理通りになるのです。
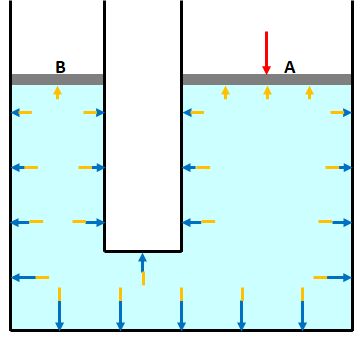
(5)シミュレーション
パスカルの原理をシミュレーションによって確かめてみましょう。
液体は圧力が生じる様子を観察するのが難しいので気体をシミュレートします。液体の場合隣接する分子が押し合うのに対し、気体の場合は分子が離れていますが、衝突によって液体と同じように力が伝わります。
容器に気体が充填されている状態では、容器の壁にかかる力は単位時間内に壁に衝突した分子の速度(の壁に垂直な成分)の和に比例します。ただし気体の分子の重さは一様とします。この力を面積で割ることによって圧力を求めています。
「重力無 上」のボタンを押してみてください。中の青い点は気体の分子です。上の面の圧力を数か所に区切って計算します。圧力は容器の上に棒グラフで表示します。各圧力はシミュレーション開始からの衝突速度の総和をシミュレーションの時間で割って求めています。
「圧力」のボタンを押すと容器の右側上面が下に移動します。これは外から力が加えられて縮んでいるところだと思ってください。
「重力無 横」のボタンを押すと側面の圧力を表示します。
同様に「重力有 上」、「重力有 横」を押すと重力がある場合をシミュレートします。
やや誤差の大きいシミュレーションですが、以下のことがわかると思います。
・重力がない場合はどの面にも同じ圧力がかかる。
・重力がある場合は高いところほど圧力が大きいが、同じ高さでは圧力も同じ。
(5)まとめ
パスカルの原理に関する問題を解く際、重力があってもなくても同じ結果が得られるはずです。ただし、それは求められている場所の高さが変わらない場合に限ります。重力があり、高さが変わる場合は、その高低差と流体の密度の積の分だけ圧力が反映されなければなりません。
