なぜ木は水に浮き、鉄は沈むのでしょう。※1 木の比重は水の比重(約1000kg/m)より小さく、鉄は大きいからですね。
ではなぜ物体の比重によって浮き沈みが決まるのでしょう。これはアルキメデスの原理によって説明できます。アルキメデスの原理が正しいことは数式を使って証明できますが、ここでは数式を使わずシミュレーションによって確認します。
(1) アルキメデスの原理とは
アルキメデスの原理を思い出しましょう。
「液体(気体)の中の物体には、その物体が押しのけている液体(気体)の重さと同じ大きさの浮力が生じる」
というものでしたね。
この浮力とは何でしょう。
水の中に物体があります。

これを水に置き換えます。

この水にかかる重力と
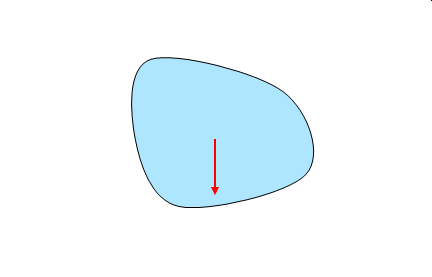
逆向きで同じ大きさの力が浮力として作用します。

物体の比重に関わらず、周囲の液体(気体)の比重によって浮力が決まります。物体にかかる重力はその比重によって決まるので、水と物体の比重を比較することによって浮くか沈むかが決まります。
(2)なぜ物体が押しのける液体(気体)の重さだけ浮力が生じる?
ではなぜこうなるのでしょう。
水の中の物体には水の圧力が加わります。水が静止している場合、この圧力は物体の面に対して垂直方向です。そして深いところほど圧力は大きく、浅いところほど小さくなります。
つまりこのように、物体の下側の面にかかる圧力は上向きで大きく、物体の上側の面にかかる圧力は下向きで小さくなります。これらを足し合わせると上向きの力、つまり浮力となるのです。
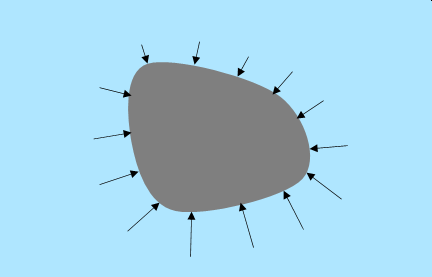
しかし、本当に物体の面にかかる圧力の和が浮力と一致するのでしょうか。また、物体の形状によって異ならないのでしょうか。
次の項でシミュレーションにて確認します。
(3)シミュレーション
水の中に多角柱の物体があるとします。底面は横を向いており、我々はこの底面を横から見ています。
「始」のボタンを押してください。ランダムに多角柱(の底面)を表示します。奥行方向に側面があると思ってください。押す度に新しい図形を表示します。
赤の矢印と数字は面にかかる圧力の和です。青の矢印と数字は物体が押しのけた水の重さです。単位はN(ニュートン)です。
(4)まとめ
多角柱だけでしたが、面にかかる圧力の総和と、領域内が水だった場合の重力が一致することが確認できました。
ここでは触れませんでしたが、この関係を解析的に検証する方法はあります。その一つはガウスの定理(発散定理)を使用する方法です。今度はなぜガウスの定理が成立するのか知りたくなるかもしれませんが、いろいろ考えてみると面白いかもしれません。
※1 ほとんどの木は細胞と細胞の間の隙間が大きいために比重が小さいのですが、細胞が密集していて比重が水より大きい木もあります。このような木は水に入れると沈みます。
