ビュフォンの針は、等間隔に直線が引かれた紙の上に針を落とすとその線が直線と交わる確率がどれだけか、という問題です。面白いのは、実際に複数の針を落として確率を求めると円周率が導かれるというところです。
針が直線と交わる確率を式で表すとその中にはπが含まれます。もし実測にて針が直線に交わる割合を求めていた場合、式にあてはめてπを数値として算出できます。モンテカルロ法に似た手順です。以下はその手順です。
(1)条件
落ちた針と直線のなす角度が小さく針がどの直線からも離れていれば交わらないことがあるし、そうでない場合は交わります。
図の青の針は直線に交わっていますが、赤は交わっていません。
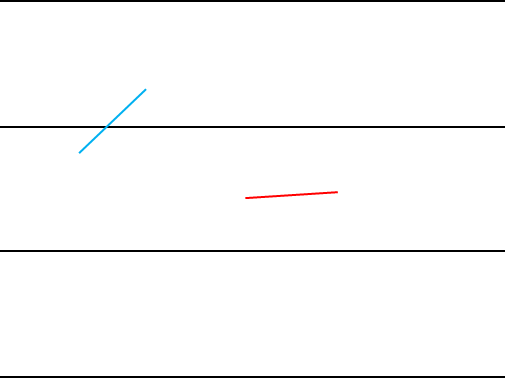
与えられている値は直線の間隔と針の長さです。針が落ちる位置と角度の確率は偏りがありません。
ここでは直線と直線の間を\(t\)、針の長さを\(l\)とします。
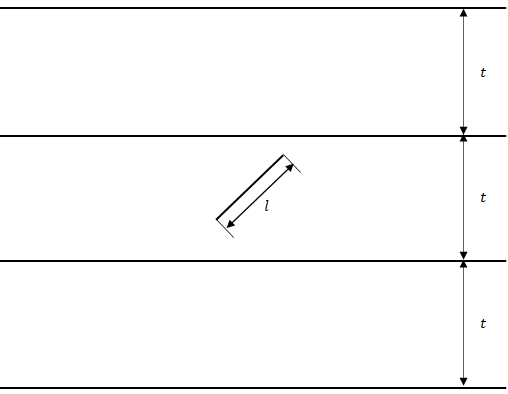
(2)針が直線と交差する確率を求めるための方針
確率を求めるため、針の中心と直線(最も近い線)の距離を\(y\)、直線と針がなす角を\(\theta\)とします。
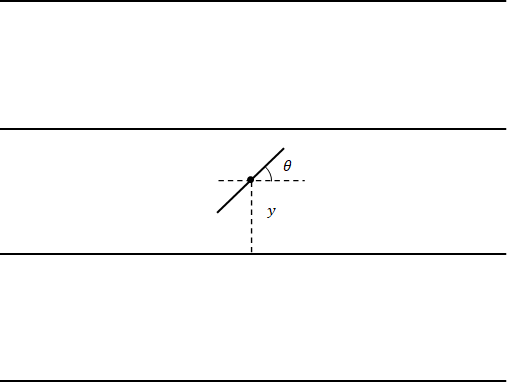
針を落とす度に変わるのはこの\(y\)と\(\theta\)です。yと\(\theta\)の値によって直線と交差するかどうかが決まります。\(y\)と\(\theta\)の分布は一様です。つまり落ちた針の縦方向の出現頻度に偏りがありません。向きも偏りません。\(y\)と\(\theta\)を変化さ、その中で交差する場合の割合を求めれば、それが確率になります。
しかし変数が2個あります。そこで片方を固定しもう片方だけが変動するとして式をたてることにします。次に固定だった変数を変動、変動だった変数を固定にします。
(3)\(\theta\)を固定とした場合
まずは\(y\)だけが変動するとします。yを変動させる範囲はどれだけでしょうか。与えられた問題の直線は等間隔に並んでいます。また、 \(\displaystyle {0 \le y \le \frac{t}{2} } \) と\(\displaystyle { \frac {t}{2} \le y \le t} \)は対称です。したがって \(\displaystyle {0 \le y \le \frac{t}{2} } \) の間で変動させた場合の確率の平均を求めることにします。
\(y\)を変化させていくと、交差している状態から交差しない状態(またはその逆)に変わる境界があります。以下の図の状態です。このときの\(y\)が\(\displaystyle{ \frac{l \sin \theta} {2} }\)です。
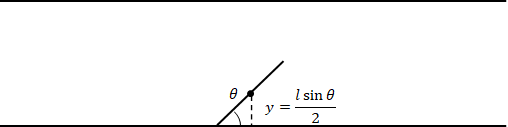
下の図は\(y\)を変動させた場合のイメージです。θはある値に固定しています。針の中心が直線上にある状態からスタートし、t/2まで移動させます。途中で交差しなくなります。
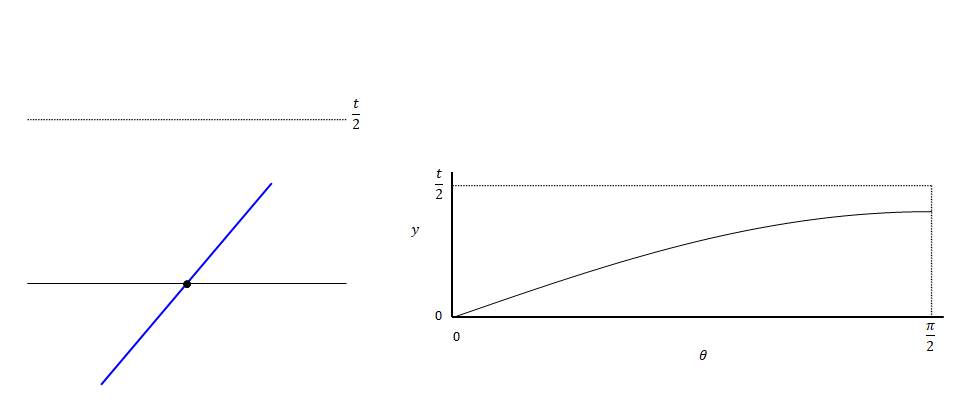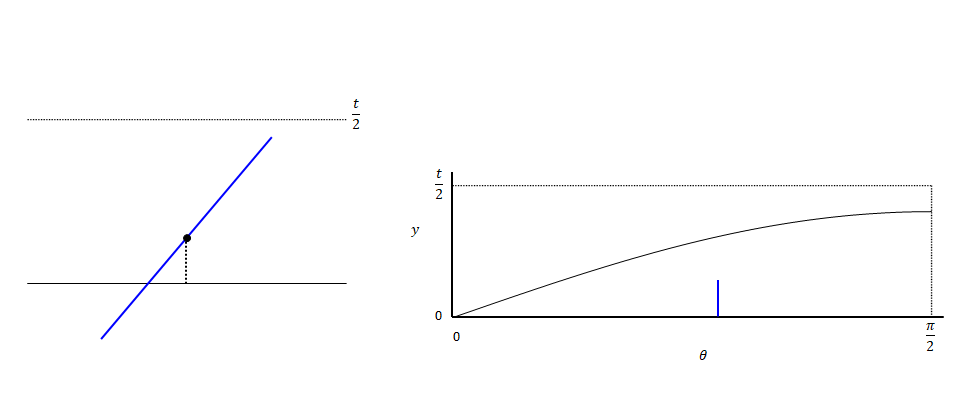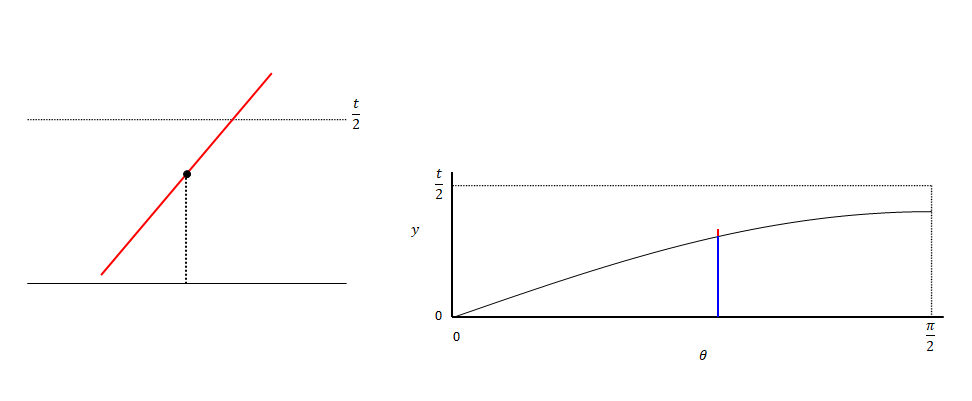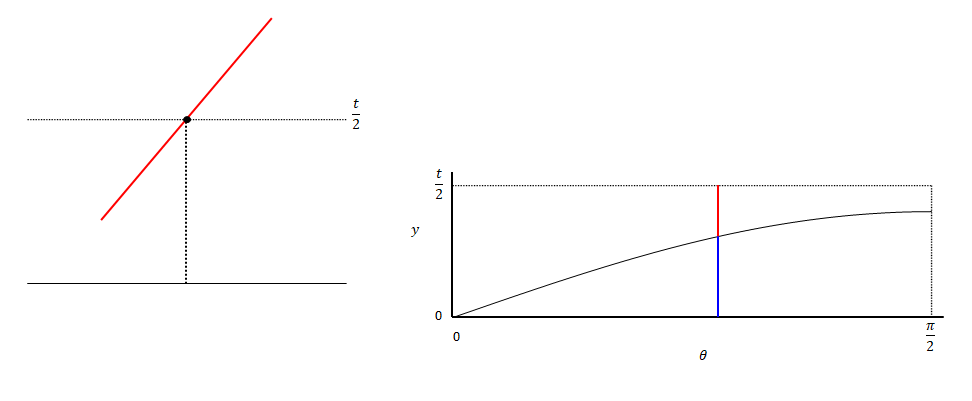
(4)\(y\)を固定とした場合
次に\(\theta\)を変動させる場合です。\(\displaystyle {0 \le \theta \le \frac{\pi} {2} }\) と\(\displaystyle {\frac{\pi}{2} \le \theta \le \pi }\) は対称です。\(\displaystyle {\pi \le \theta \le \frac{3\pi} {2} }\) 、\(\displaystyle {\frac{3\pi}{2} \le \theta \le 2\pi }\)も同様です。したがって、\(\displaystyle {0 \le \theta \le \frac{\pi} {2} }\)の範囲のみを考慮します。
下の図は\(\theta\)を変えた場合のイメージです。\(\theta\)が0の状態では交差しません。値を大きくしていくと途中で交差するようになります。
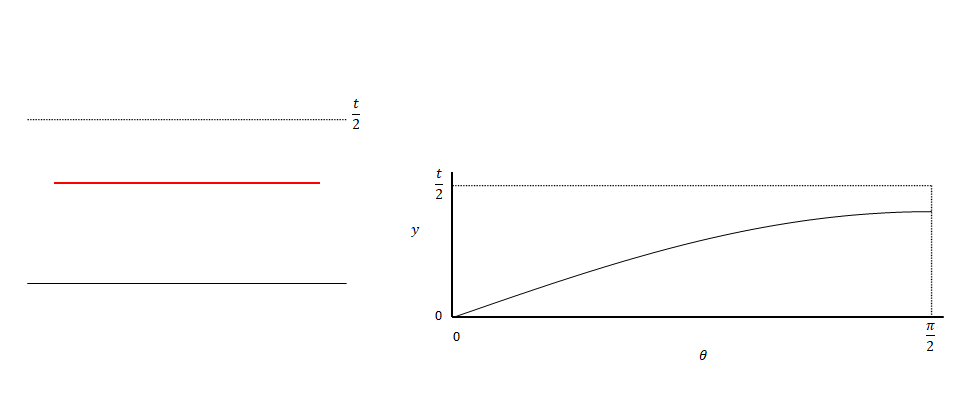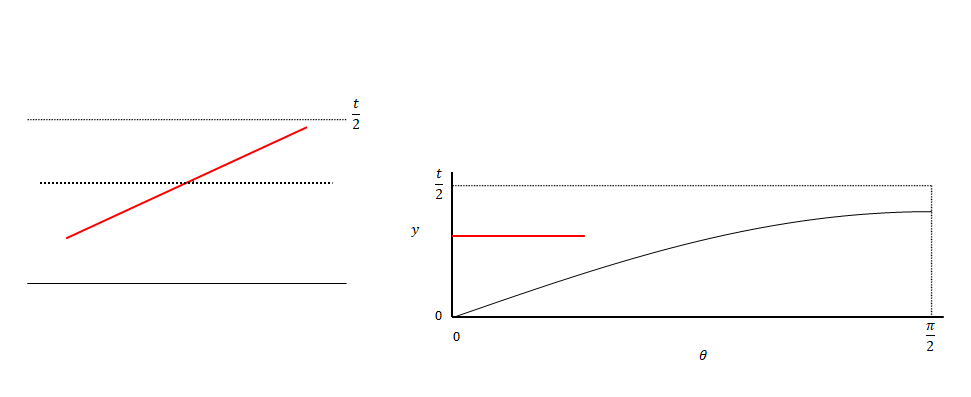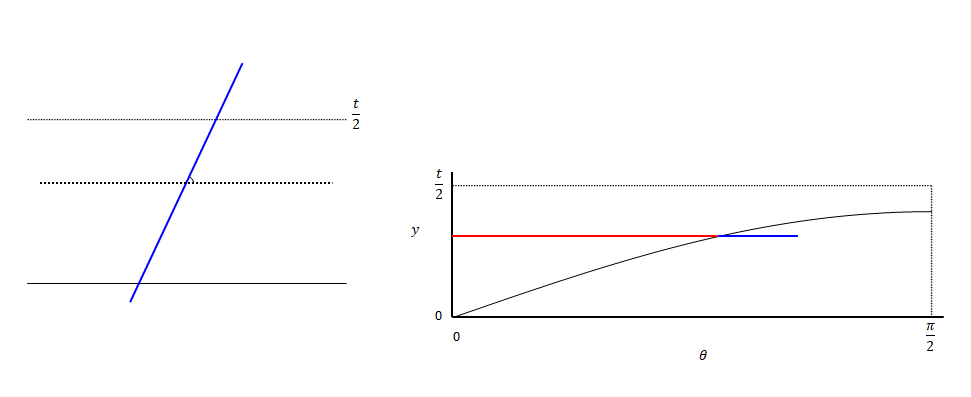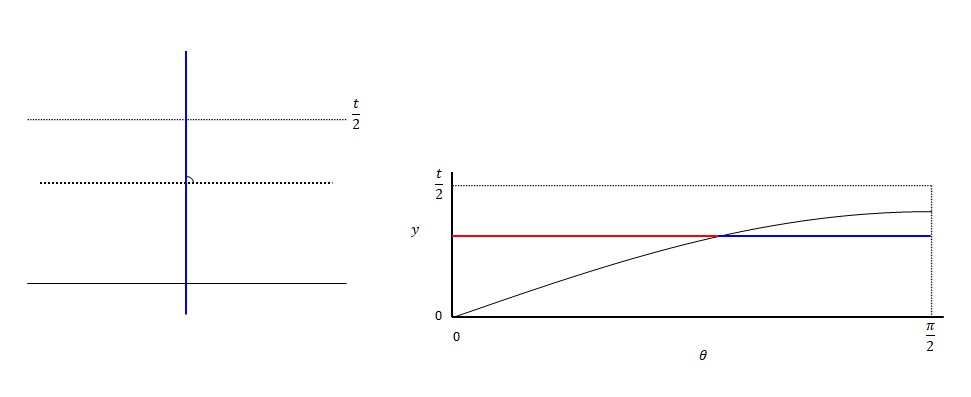
つまり、交差する領域は以下です。全体(赤+青)に対する青の面積の割合が交差する確率です。
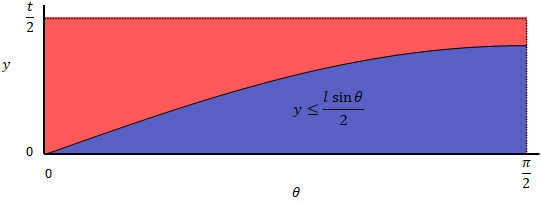
この青の面積は、
$$\int^{\frac{\pi}{2}} _{0} \frac{l sin \theta}{2} d\theta = \frac{l}{2}$$
赤+青の面積は、
$$ \frac{\pi}{2} \times \frac{t}{2} = \frac{\pi t}{4}$$
青の面積の割合は、
$$ \frac{\frac {l}{2}} {\frac{\pi t}{4}} = \frac{2 l}{\pi t}$$
となります。これが針が交差する確率の式です。
(5)式と実測値より円周率を求める
求められた式を実測値と等しいとすれば円周率を求めることができます。
実際に針を落として交差した割合を r とすると以下の関係になります。
$$ \frac{2 l}{\pi t} \simeq r $$
したがって円周率は以下です。
$$ \pi \simeq \frac {2l}{rt}$$
(6)シミュレーション
以下はシミュレーションの結果です。横軸は実行回数、縦軸は確率です。ページを開いた時点で既に開始しています。再実行する場合は「再実行」を押してください。
3.14に近い値に収束することがわかると思います。
