円周率の求め方にはいくつか方法がありますが、いずれも簡単ではありません。ただし一つだけ簡単に求める方法があります。モンテカルロ法です。この方法のユニークなところは無作為に選んだ値を用いるところです。以下、その方法です。
正方形と、内接する円を描きます。

正方形の内側にランダムに点を加します。
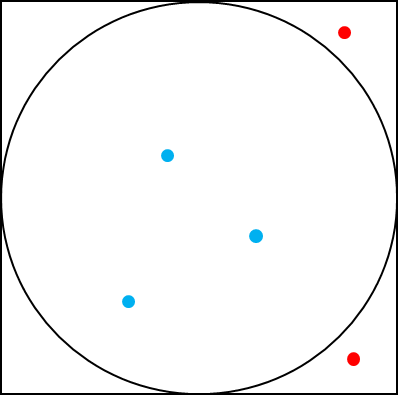
円の内側の点(図では青)と正方形の内側の(赤と青)を数えます。この点の比を正方形と円の面積の人とみなせば、点の数がこれと等しいことになります。
同時に理論上の円と正方形の面積の比は円周率を用いて表すことができます。こしたがって下図のように求められます。
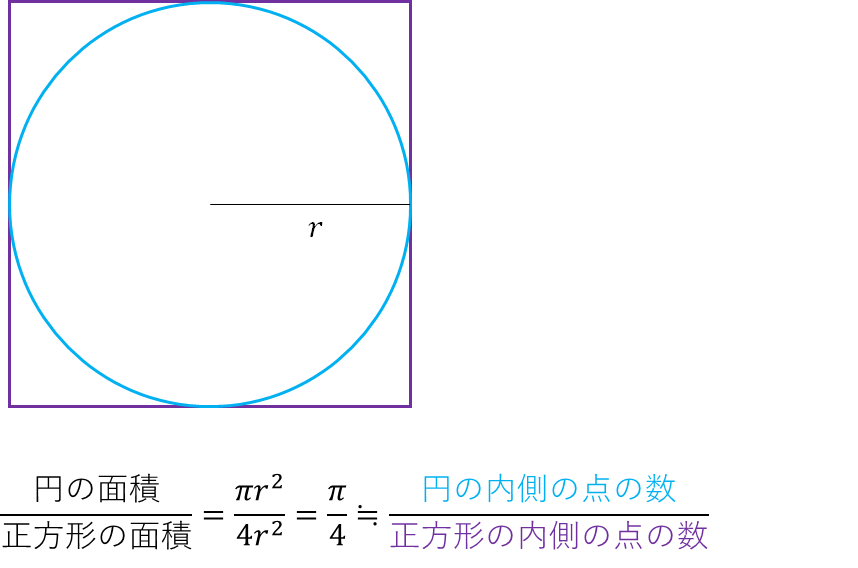
この場合は正方形の内側の点の数は5、円の内側の点の数は3なのでπは2.4という、誤差の大きい結果になりました。
しかし、誤差が大きかったのはサンプル数が少なかったからです。大数の法則が示す通り、サンプル数を増やせば誤差を小さくすることができます。
モンテカルロ法はコンピューターでシミュレートすることができます。以下がその結果です。
ページを表示した時点より実行を開始しています。再実行する場合は「再実行」ボタンを押してください。
